Теорема Чебышева.

Теорема Чебышева:Пусть 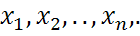- независимые СВ с конечными мат. ожиданиями 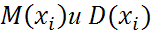, причем 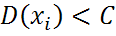, тогда

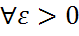
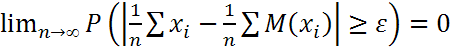
Опр.t wx:val="Times New Roman"/><w:i/><w:sz w:val="40"/><w:sz-cs w:val="40"/></w:rPr><m:t>в†’</m:t></m:r><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="40"/><w:sz-cs w:val="40"/><w:lang w:val="EN-US"/></w:rPr><m:t>X</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 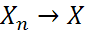по вероятности, если .

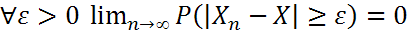Доказательство: Рассмотрим СВ 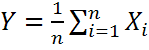. Найдем мат. ожидание и дисперсию: 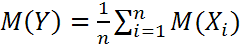; 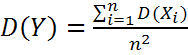. Применим неравенство Чебышева: 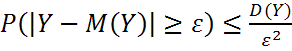; 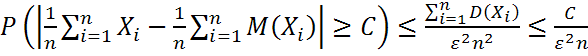. Пусть 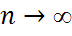и получаем утверждение теоремы.