Центральная предельная теорема.

Опр: Пусть 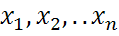- СВ. Случ. величину 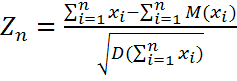– нормированная сумма. Если 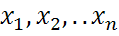-независимые СВ, то 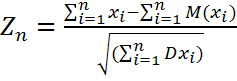. если 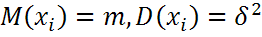, 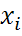- одинаково распределены, то .

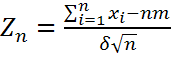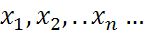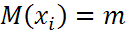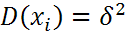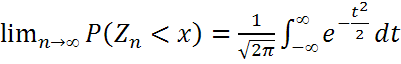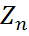Теорема:Если - независимые СВ , имеющие один и той же закон распределения с мат. ожидания , , то . - распределена асимметрически при 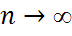по стандартному норм. закону. .

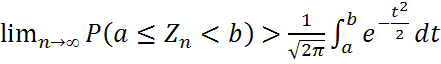Доказательство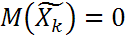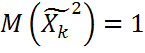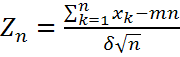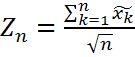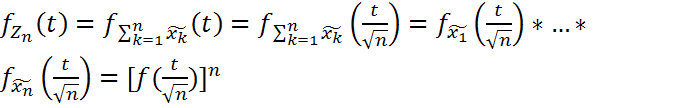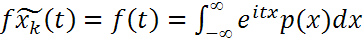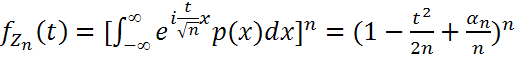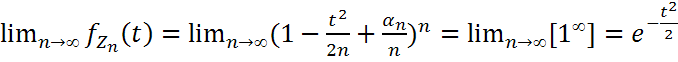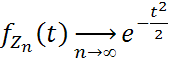: , ; ; ; ; ; ; . - хар-ая функция стандартного нормального закона распределения. Последовательность функций распределения СВ 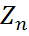сходится к функции распределения стандартного нормального закона распределения. Это равносильно утверждению теоремы. доказано.