Распределение c2

DfПусть X1,…,Xn-незав.СВ.,распред.нормально смат.ожиданием m=0 и дисперсией .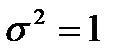

СВ 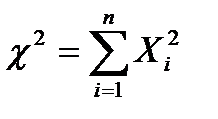с ν=n ст.св.Плотность распр-ия имеет вид: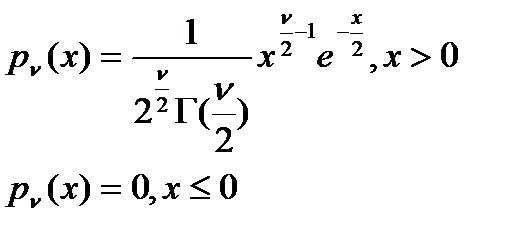

Г-гамма-функция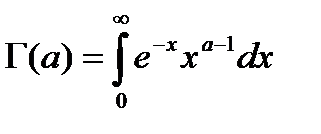

Функция распределения:

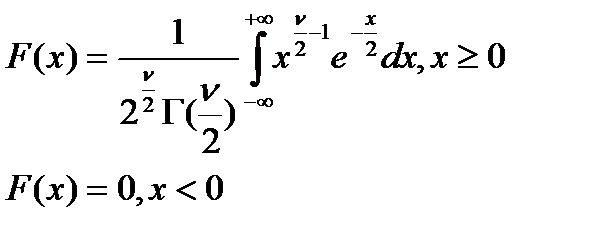
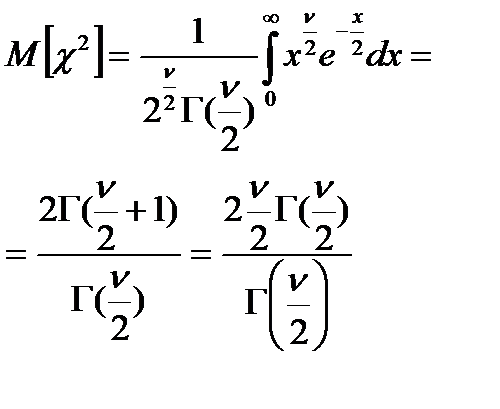
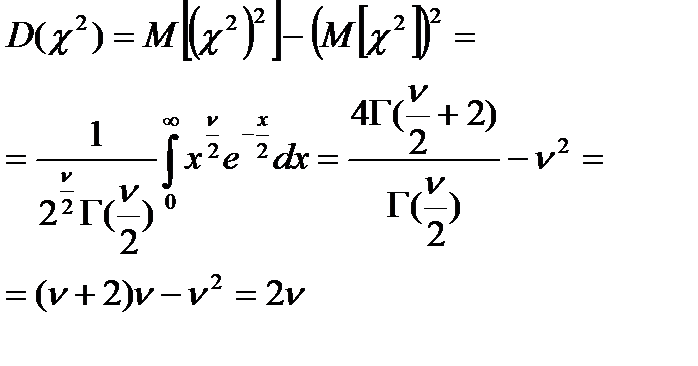
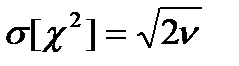
Теорема.Пусть X1,…,Xn-СВ,распр.норм.содинаковыми мат.ож. m и дисперсиями .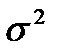

Тогда:1)СВ 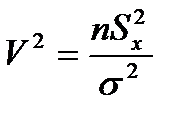имеет распр.c2 с n=n-1.

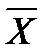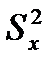2)СВ и явл.незав.

Замечание : СВ 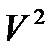м.б.представлена в ви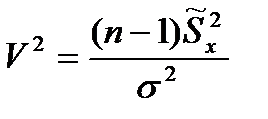де где 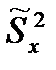-исправленная дисперсия

При нахождении вер-ти того,что дисперсия выборки 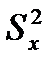примет зн-иеи з отр.{a;b} т.е 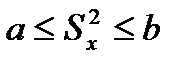Преобразуется к виду:

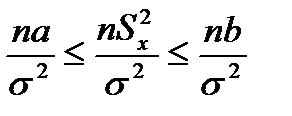
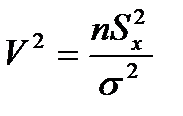распр. по з-ну c2 с n=n-1

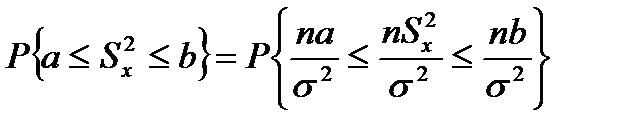
Для n<=30 составлена таблица 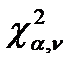где α-уровень вер-ти.

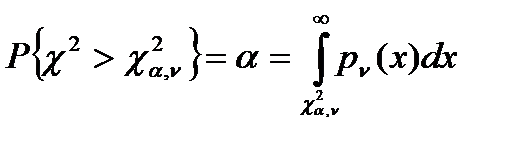
Зн-ие .c2 наз квантилью распр-ия,отвеч.заданому уровню вер-ти

И заданному числу ст.свободы.

При n>30 и a<=0.5 применяют такую ф-лу:

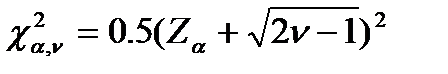где 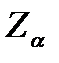это квантиль норм.распр. с m=0 и s=1.

Через ф-цию Лапласа:

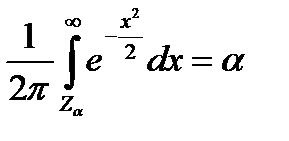
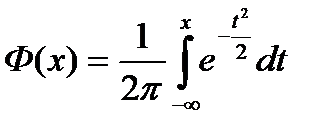
Ф(Za)=1-a