Доверительный интервал для дисперсии нормально распределеннной С.В.
Найдем доверительный интервал с заданной доверительной вероятностью 1-α для дисперсии 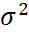 нормально распределенной С.В. Х.
нормально распределенной С.В. Х.
В силу теоремы1 и замечания1 из пункта распределение Хи квадрат С.В.: 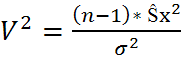 имеет распределение
имеет распределение 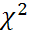 с
с 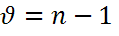 степенями свободы.
степенями свободы.
Выберем с1 и с2 такие что
P( 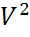 <c1)=
<c1)= 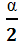 иP(
иP( 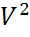 >c2)=
>c2)= 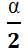 Тогда P(
Тогда P( 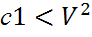 <c2)=
<c2)= 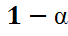
По таблице ищем распределение Хи квадрат(квантилей)
С2= 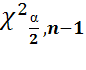 P(
P( 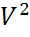 <c1)=1- P(
<c1)=1- P( 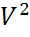 >c1) следовательно P(
>c1) следовательно P( 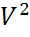 >c1)=1-
>c1)=1- 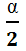 С1=
С1= 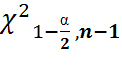 С1<
С1< 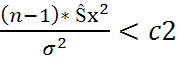 т.т.т,когда
т.т.т,когда 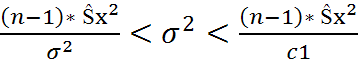
P( 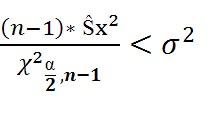 <
< 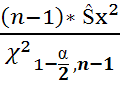 )=
)= 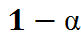
Т.о. искомый доверительный интервал имеет вид: ( 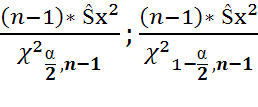 )
)
43.ПРОВЕРКА ГИПОТЕЗ О ЗАКОНЕ РАСПРЕДЕЛЕНИЯ. КРИТЕРИЙ СОГЛАСИЯ 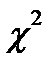 (Пирсона).
(Пирсона).
Ранее рассматривались гипотезы, относящиеся к отдельным пар-рам С.В. При этом закон распределения предполагался известным. Теперь рассмотрим критерий критерии согласия, которые применяются для проверки гипотез о том, что распределение изучаемой С.В., подчиняется некоторому извест-ному закону распре-деления, т.е. о кри-териях, кот. Позво-ляют по данным выборки определить распределена ли С.В. по некоторому закону распределе-ния [известному]  .
.
Пусть 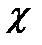 исследуемая С.В. и тре-буется проверить гипотезу
исследуемая С.В. и тре-буется проверить гипотезу 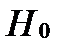 о том, что эта С.В. распределена по закону распределения
о том, что эта С.В. распределена по закону распределения 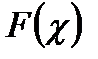 [известная функция].
[известная функция].
Для проверки гипотезы проводиться выборка, состоящая из 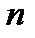 наблюдений за
наблюдений за 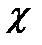 . По выборке можно построить эмпирическое распределение. Срав-нение эмпирических и теоретических распределений производятся с помо-щью специально подобранной С.В. критерия согласия. Существует несколько критериев согласия:
. По выборке можно построить эмпирическое распределение. Срав-нение эмпирических и теоретических распределений производятся с помо-щью специально подобранной С.В. критерия согласия. Существует несколько критериев согласия: 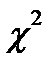 (Пирсона), Колмогорова и др.
(Пирсона), Колмогорова и др.
1. Критерий согласия 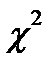 (Пирсона)
(Пирсона)
Пусть 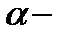 заданный уровень значи-мости. Множество зн-ний С.В.
заданный уровень значи-мости. Множество зн-ний С.В. 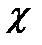 разобьем на
разобьем на 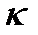 непересекающихся частей
непересекающихся частей 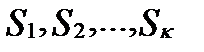 . Эти множества представляют собой интервалы - для непр. С.В. – либо группы отдельных зн-ний – для дискретной С.В.
. Эти множества представляют собой интервалы - для непр. С.В. – либо группы отдельных зн-ний – для дискретной С.В.
Предполагая известным теорети-ческий закон распределения 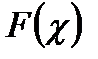
можно для каждого 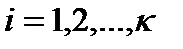 определить теоретическую вероятность
определить теоретическую вероятность 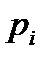 попадания С.В.
попадания С.В. 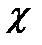 в множество
в множество 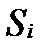 .Тогда теоретическое число значе-ний С.В.
.Тогда теоретическое число значе-ний С.В. 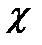 попавших в множество
попавших в множество 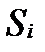 , можно рассчитать по формуле
, можно рассчитать по формуле 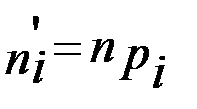
Эмпирические частоты будем обозначать 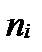 . Если эмпирические частоты сильно отличаются от теоре-тических, то проверяемую гипоте-зу
. Если эмпирические частоты сильно отличаются от теоре-тических, то проверяемую гипоте-зу 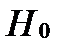 следует отвергнуть. А в против-ном случае принять. Пирсон доказал, что при
следует отвергнуть. А в против-ном случае принять. Пирсон доказал, что при 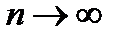 статистика
статистика 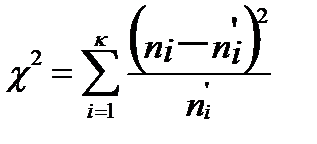
 имеет распределение
имеет распределение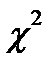 с
с 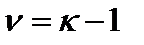 степенями свободы. Но это имеет место, если все параметры распределения
степенями свободы. Но это имеет место, если все параметры распределения 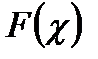 предполагаются извест-ными.
предполагаются извест-ными.
Если же параметры распределения 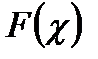 оцениваются по выбо-рке, то С.В.
оцениваются по выбо-рке, то С.В.  при
при 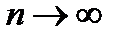 имеет распреде-ление
имеет распреде-ление 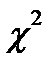 с
с 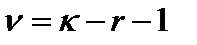 сте-пенями свободы, где
сте-пенями свободы, где 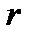 - это число параметров распределения
- это число параметров распределения 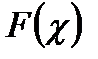 , оцениваемых по выборке. Таким образом, в качестве меры расхождения м/у
, оцениваемых по выборке. Таким образом, в качестве меры расхождения м/у 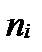 и
и 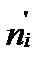 исп. крите-рий
исп. крите-рий  .Правило применения
.Правило применения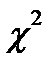
рассчитываем значение 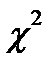 по выбор-ке. По таблице
по выбор-ке. По таблице 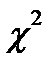 - распределения определяем зн-ние
- распределения определяем зн-ние 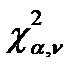 .Если
.Если 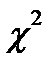 >
> 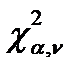 , то гипотеза
, то гипотеза 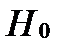 отвер-гается. В противном случае
отвер-гается. В противном случае 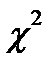
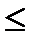
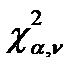 ,то гипотеза
,то гипотеза 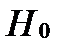 принимается.
принимается.
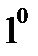 Т.к. статистика
Т.к. статистика  имеет
имеет 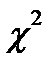 - распределение лишь при
- распределение лишь при 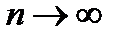 , то необходимым условием применения критерия
, то необходимым условием применения критерия 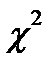 (Пирсона) явл. выпол-нение нер-ва
(Пирсона) явл. выпол-нение нер-ва 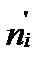
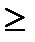 5. Если
5. Если 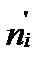 <5,то нужно объединить множества
<5,то нужно объединить множества 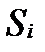 так, чтобы
так, чтобы 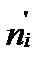
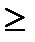 5 выполнялось.
5 выполнялось.
 Таблица
Таблица 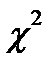 - распределения соста-влена для числа степ. свободы
- распределения соста-влена для числа степ. свободы 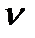 <30, то используется следующая ТЕОРЕМА ФИШЕРА: величина
<30, то используется следующая ТЕОРЕМА ФИШЕРА: величина 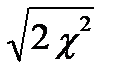 при
при 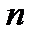 степенях свободы распределена асимп-тотически [при
степенях свободы распределена асимп-тотически [при 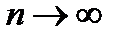 ] нормально с мат. ожиданием
] нормально с мат. ожиданием 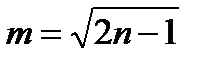 и диспе-рсией
и диспе-рсией 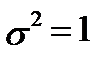 .
.
Дата добавления: 2015-06-27; просмотров: 701;
