Независимые случайные величины. Критерий независимости.
Опр:СВ 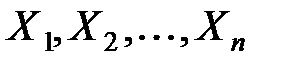 называются независимыми, если закон распределения любого числа из них не зависит от того, какие возможные значения приняли остальные величины.
называются независимыми, если закон распределения любого числа из них не зависит от того, какие возможные значения приняли остальные величины.
Равносильное опр:СВ 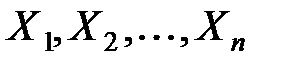 называются независимыми (совокупностями), если для любого набора событий {
называются независимыми (совокупностями), если для любого набора событий { 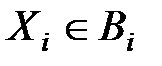 }(i=1,2,3…n) где
}(i=1,2,3…n) где 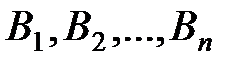 произвольные подмножества числовой оси, выполняется равенство:
произвольные подмножества числовой оси, выполняется равенство: 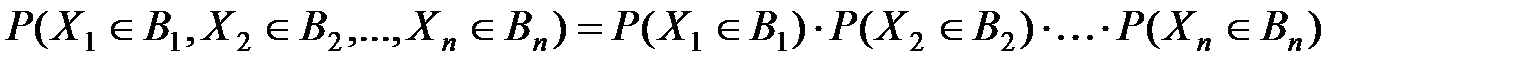 .
.
Для дискретной СВ равносильное определение: дискретные случайные величины 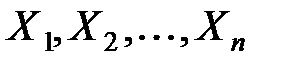 называются независимыми, если для любых значений
называются независимыми, если для любых значений  случайного вектора (
случайного вектора ( 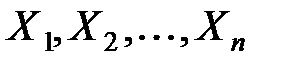 ) выполняется равенство:
) выполняется равенство:
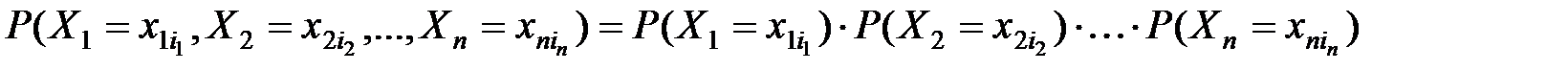
Для непрерывных СВ 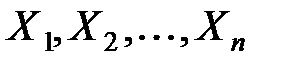 :
:
Непрерывные СВ 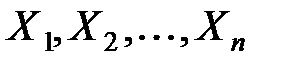 называются независимыми, если
называются независимыми, если  интервалов числовой оси выполняется равенство:
интервалов числовой оси выполняется равенство: 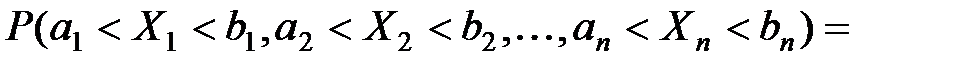
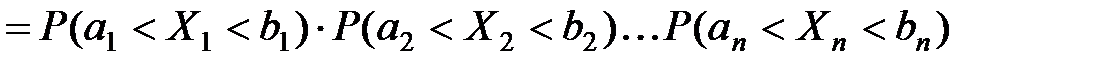
Теорема 1:случайные величины 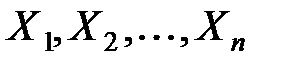 независимы т.т.т., когда в любой точке (
независимы т.т.т., когда в любой точке ( 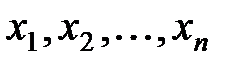 ) имеет место равенство:
) имеет место равенство: 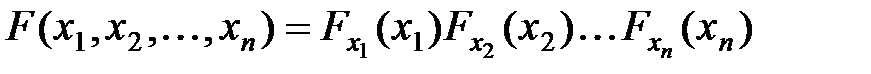
Теорема 1:непрерывные СВ 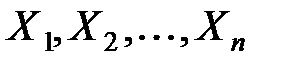 независимы
независимы  когда выполняется равенство:
когда выполняется равенство: 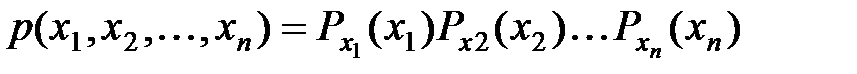
Док-во:  Х, У -независимые СВ
Х, У -независимые СВ

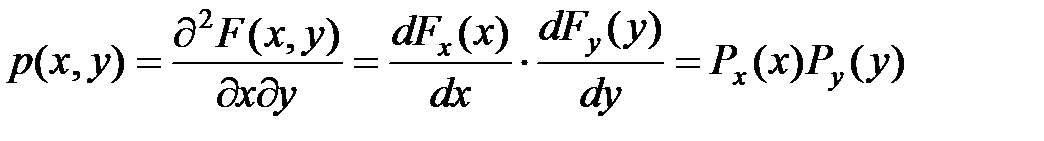
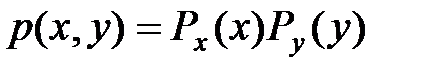
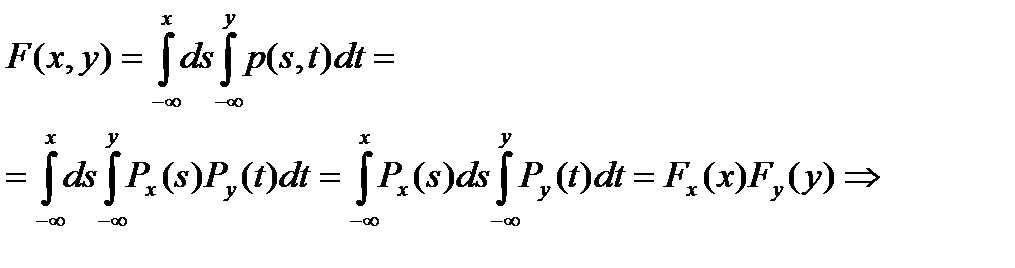 по теореме 1 события Х и У независимые. x
по теореме 1 события Х и У независимые. x
Для дискретной СВ: 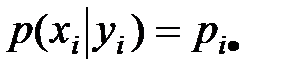

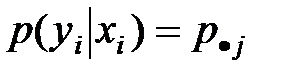
Для непрерывн СВ Х,У:
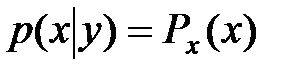
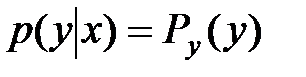
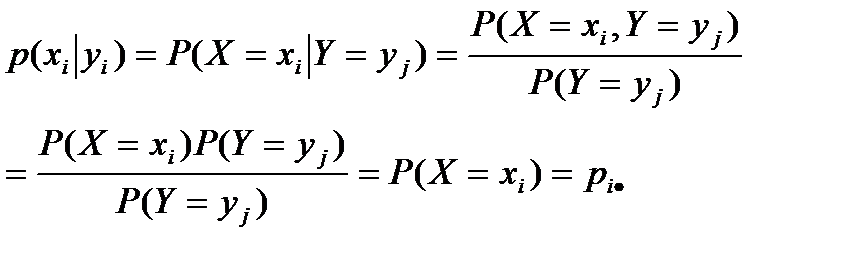
Дата добавления: 2015-06-27; просмотров: 1168;
