Определение расстояний до ориентира по измеренному вертикальному углу. Определение места судна по расстояниям. Комбинированные способы определения места судна.
Расстояния в море могут определяться несколькими визуальными методами: с помощью дальномеров, глазомерно, по вертикальному углу. Дальномеры работают на основе различных принципов. Горизонтально-базисные решают треугольник по известной стороне (базе дальномера, которой является труба прибора) и измеряемому горизонтальному углу. Стереоскопические используют свойство человеческого глаза различать глубину пространства. Микрометрические используют известную высоту предмета и противоположный угол. Точность измерения зависит от базы и измеряемого расстояния, ошибки увеличиваются пропорционально квадрату расстояния. На судах торгового флота дальномеры не нашли широкого применения. Здесь используется метод определения расстояния по вертикальному углу, измеренному секстаном.
При этом могут быть 3 варианта:
1. Определение расстояния до ориентира, основание которого расположено ближе видимого горизонта, а сам ориентир находится недалеко от уреза воды ( высота ориентира больше расстояния от него до уреза воды) .
Секстаном измеряется либо угол между основанием и вершиной ориентира, либо угол между вершиной ориентира и урезом воды у береговой черты под ориентиром.Последний вариант применяется чаще всего, так как основание ориентира может быть закрыто растительностью, скалами и т.д.(нераспознаваемо). Однако, следует помнить, что в этом случае при плавании в морях с приливами нужно учитывать уровень воды (вычитать уровень прилива из указанной в навигационных пособиях высоты маяка).
| D |
| h |
| α |
Предположим, что высота ориентира известна, а высота глаза наблюдателя равна нулю. Тогда расстояние до ориентира определится из прямоугольного треугольника по формуле:
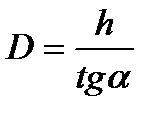
Так как угол α весьма мал (измеряется минутами, редко достигая нескольких градусов с минутами), величину 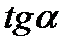 можно заменить величиной α, при условии, что угол α взят в радианах. Так как высота ориентира берётся в метрах, то и дистанцию до него по этой формуле получаем в метрах. Для перехода от метров к милям разделим числитель на 1852, а чтобы перейти от радианов к минутам (угол секстаном измеряется в градусах и минутах) знаменатель разделим на
можно заменить величиной α, при условии, что угол α взят в радианах. Так как высота ориентира берётся в метрах, то и дистанцию до него по этой формуле получаем в метрах. Для перехода от метров к милям разделим числитель на 1852, а чтобы перейти от радианов к минутам (угол секстаном измеряется в градусах и минутах) знаменатель разделим на 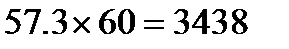 .
.
Тогда: 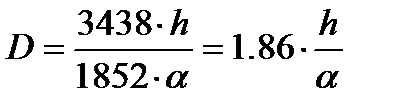 (1)
(1)
Высоту маяка можно взять либо с карты (на всех английских картах и на некоторых российских высоты маяков нанесены около них), либо – из пособия «Огни и знаки». В последнем случае приводится как высота ориентира от основания, так и высота от уреза воды.
Рефракция для основания и вершины маяка приблизительно одинакова, поэтому не учитывается. Угол α находится по формуле: 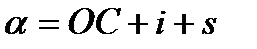 .
.
Влияние высоты глаза наблюдателя на определяемую дистанцию до ориентира.
| h |
| e |
| h-e |
| D |
| C |
| α |
| α |
Если глаз наблюдателя находится на некоторой высоте е, то формула для определения дистанции даёт ошибку С. Её величина находится на основе свойства секущих к окружности, вмещающей измеренный вертикальный угол, а также вершину и основание ориентира (урез воды):
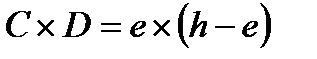 , откуда:
, откуда:
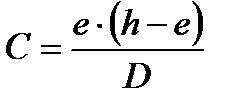 .
.
Из формулы видно, что при 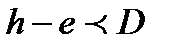 ошибка в дистанции не превышает высоты глаза наблюдателя, т.е., составляет всего несколько метров. Таким образом, в большинстве случаев она незначительна и может не учитываться. Если всё-таки необходимо учесть ошибку, то:
ошибка в дистанции не превышает высоты глаза наблюдателя, т.е., составляет всего несколько метров. Таким образом, в большинстве случаев она незначительна и может не учитываться. Если всё-таки необходимо учесть ошибку, то:
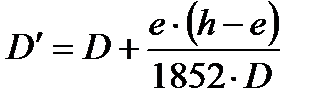
2. Определение расстояния до ориентира, когда урез воды находится ближе видимого горизонта, а основание ориентира удалено от уреза воды на некоторое расстояние L.
В этом случае также секстаном измеряется вертикальный угол между урезом воды и вершиной ориентира. Дистанция от уреза воды до ориентира снимается с карты. Этот способ часто применяется при определении дистанции до вершины горы, нанесённой на карту и обозначенной на ней в качестве ориентира.
В данном случае: 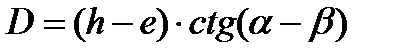
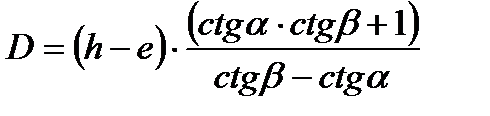
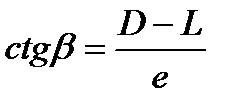
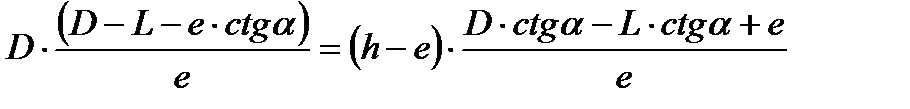
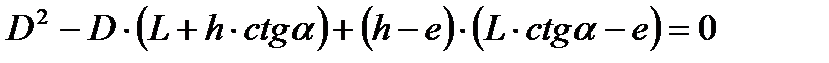
| h |
| β |
| e |
| D |
| L |
| α |
| N |
| A |
| O |
| B |
Как известно, квадратное уравнение вида: 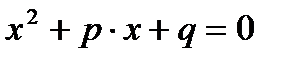
имеет решение: 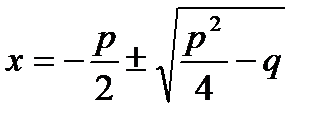 , поэтому:
, поэтому:
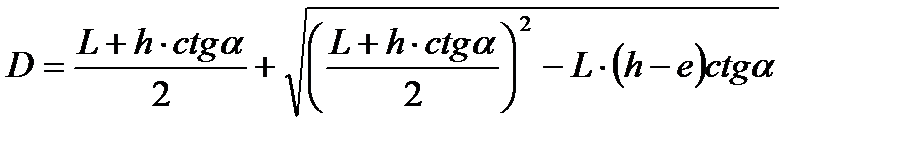
 .
.
Естественно, величины L, h и e должны быть в одних и тех же единицах.
3. Определение расстояния до ориентира, когда его основание находится за горизонтом.
| Е |
| D |
| R |
| R |
| e |
| h |
| Плоскость истинного горизонта |
| d |
| β0 |
| r |
| α |
| О |
| С |
| М |
Из-за рефракции направления на видимый горизонт и вершину ориентира определяются касательными к световым лучам, идущим по дуге от глаза наблюдателя к видимому горизонту и вершине ориентира. Тогда для определения расстояния до ориентира в угловой мере из треугольника ОСЕ на основании теоремы синусов:
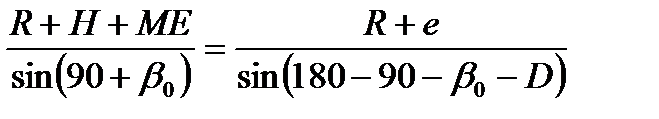
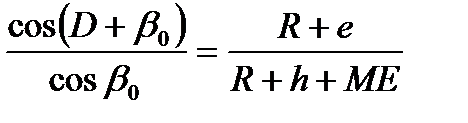
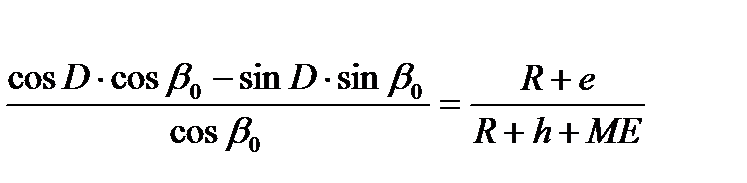
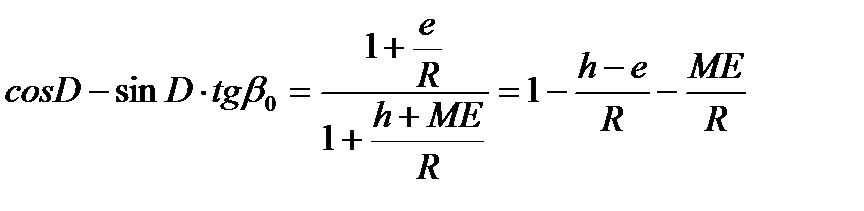
Заменив 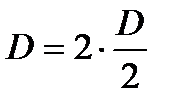 и выразив МЕ через известные величины
и выразив МЕ через известные величины
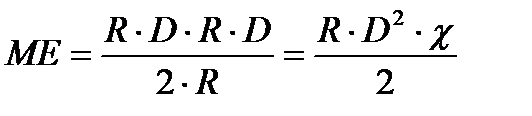 , где
, где 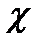 - коэффициент рефракции, получим:
- коэффициент рефракции, получим:
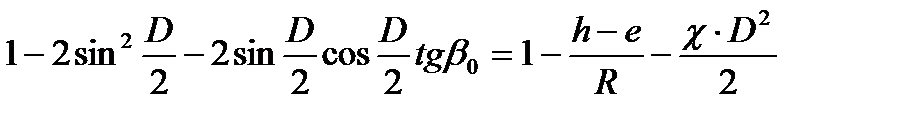
Приняв по малости D 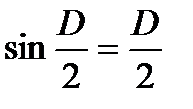 ,
, 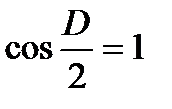 , получим:
, получим:
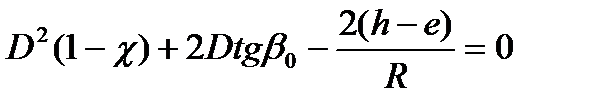
Решение этого уравнения даёт:
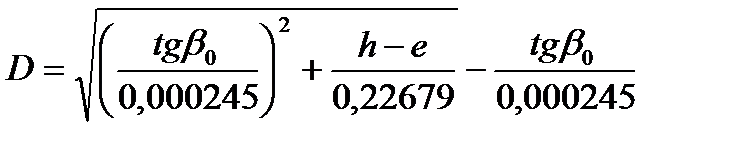 ,
,
где 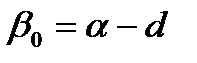
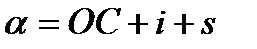
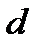 - наклонение видимого горизонта.
- наклонение видимого горизонта.
По этой формуле рассчитана таблица 29 в МТ-75. Для того, чтобы ею воспользоваться, необходимо по таблице 11-а МТ-75 в зависимости от высоты глаза или с помощью наклономера найти наклонение видимого горизонта и вычесть его абсолютное значение из измеренного секстаном угла между направлением на видимый горизонт и направлением на вершину ориентира. С полученным углом β0 и разностью 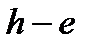 и входят в таблицу.
и входят в таблицу.
В случае, когда основание ориентира находится ближе видимого горизонта, также можно воспользоваться табл. 29. В этом случае при вычислении 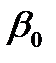 вместо наклонения видимого горизонта необходимо принимать наклонение зрительного луча, найденное по таблице 11-б МТ-75. Но, так как наклонение зрительного луча зависит не только от высоты глаза, но и от расстояния до объекта, которое нас в конечном итоге и интересует, приходится делать несколько приближений. Для начала при использовании табл. 11-б берём расстояние от счислимой точки до ориентира, затем входим в эту таблицу с расстоянием, найденным по табл. 29, и так до тех пор, пока последнее не перестанет меняться.
вместо наклонения видимого горизонта необходимо принимать наклонение зрительного луча, найденное по таблице 11-б МТ-75. Но, так как наклонение зрительного луча зависит не только от высоты глаза, но и от расстояния до объекта, которое нас в конечном итоге и интересует, приходится делать несколько приближений. Для начала при использовании табл. 11-б берём расстояние от счислимой точки до ориентира, затем входим в эту таблицу с расстоянием, найденным по табл. 29, и так до тех пор, пока последнее не перестанет меняться.
Для того, чтобы определить, что мы видим при измерении вертикального угла – видимый горизонт или урез воды, необходимо воспользоваться формулой для определения дальности видимого горизонта: 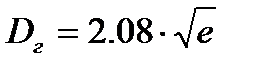 . Проведя окружность с центром в счислимогом месте и радиусом, равным
. Проведя окружность с центром в счислимогом месте и радиусом, равным 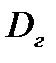 , смотрим, попадает ли внутрь неё ориентир. Если попадает – пользуемся формулой (1) , не попадает – МТ-75.
, смотрим, попадает ли внутрь неё ориентир. Если попадает – пользуемся формулой (1) , не попадает – МТ-75.
Случайные ошибки в определении расстояния до ориентира по вертикальному углу.
Градиент вертикального угла (см. определение места судна по двум горизонтальным углам) равен: 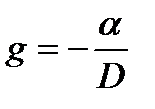 .
.
Тогда, случайная ошибка в полученной дистанции до ориентира из-за ошибки при измерении вертикального угла будет равна:
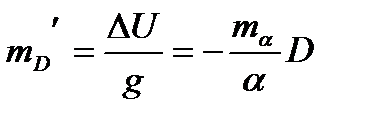
Случайная ошибка в полученной дистанции из-за ошибки в высоте ориентира по причине колебаний уровня моря:
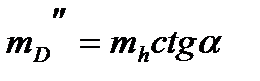
Общая ошибка:
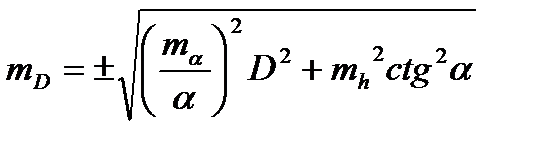
Поскольку 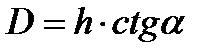 ,
,
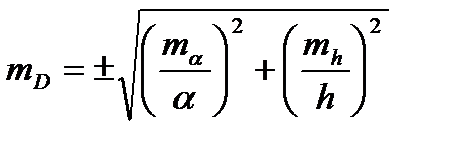
Из формулы видно, что выгоднее определять расстояния по более близким предметам с большой высотой.

Дата добавления: 2015-06-22; просмотров: 2357;
