Формулы аналитического счисления

Кроме графического счисления учёт движения судна может производиться по формулам аналитическим методом. Аналитическим счислением называется вычисление приращений к исходным координатам за счёт движения судна для получения счислимых координат на заданный момент времени.

Аналитическое счисление применяется:

1. при плавании вдали от берегов, когда ведение прокладки на мелкомасштабных картах будет неточным из-за больших погрешностей графических построений;

2. при решении астрономических задач для вычисления счислимых координат;

3. при вычислении обсервованных координат при разновременных линиях положения для приведения их к одному моменту.

Рис. 4.35. Разность широт и разность долгот

Выведем основные формулы аналитического счисления.

Судно вышло из пункта отхода А с известными координатами j₁, l₁ (рис.4.35) и, следуя постоянным курсом К по локсодромии, пришло в пункт прихода В с координатами j₂, l₂. Если будут известны сделанные судном РШ и РД, то координаты пункта В получим из соотношений

j₂ = j₁ + РШ и (4.71)

l₂ = l₁ + РД. (4.72)

Значения РШ и РД можно рассчитать по известным элементам движения: К -курсу судна и S - расстоянию, пройденному судном. Примем Землю за сферу и рассмотрим элементарный DАa¢ b¢:

Аа¢ = dj, Ab¢ = dS и a¢ b¢ = dl cоsj = dw,

где dw - расстояние между меридианами по параллели от точки а¢ до b¢, мор. мили; dS - расстояние, пройденное судном по локсодромии между точками А и b¢, мор.мили; dj - разность широт, мор.мили.

Считая элементарный DАa¢ b¢ плоским, напишем дифференциальные уравнения: dj = dS cos K и dw = dS sin K.

В результате интегрирования при К = const получим ,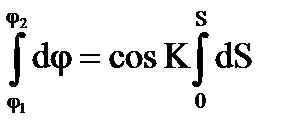

j₂ - j₁ = S cos K или РШ = S cos K. (4.73)

Для интегрирования dl сosj необходимо использовать теорему о среднем значении интеграла, вынеся cosj за знак интеграла и отнеся его к параллели некоторой промежуточной широты j_п:

,

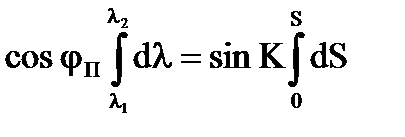(l₂ - l₁) сos j_п = S sinK.

Обозначим (l₂ - l₁) сos j_п = w и назовём эту величину отшествием (ОТШ). Тогда

ОТШ = w = S sin K. (4.74)

В геометрическом смысле ОТШ это отрезок параллели некоторой промежуточной широты j_п, заключённый между меридианами пунктов отхода и прихода, выраженный в морских милях.

Уравнение локсодромии для Земли - сферы

РД = tgК РМЧ. (4.75)

Для вывода прямой связи между ОТШ и РД снова воспользуемся теоремой о среднем значении интеграла:

ОТШ = РД cosj_п,

откуда РД = ОТШ secj_п. (4.76)

Из формулы (4.76) найдём значение промежуточной широты sec j_п = РД / ОТШ. Подставим значение РД и ОТШ из формул (4.75) и (4.74), получим

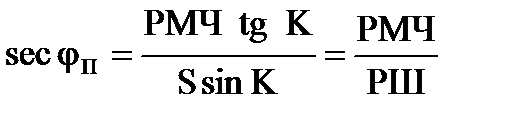. (4.77)

И тогда 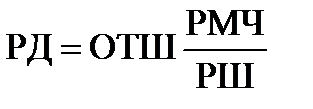. (4.78)

Рис. 4.36. Решение прямоугольного треугольника

.

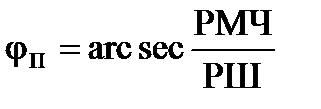На коротких переходах можно считать, что в интервале от j₁ до j₂ значение cosj изменяется линейно, тогда

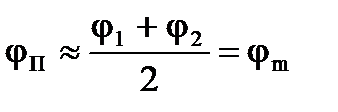
Тогда приближённая формула РД будет

РД = ОТШ sec j_m. (4.79)

По формулам (4.73) и (4.74) составлена таблица 2.19а “Разность широт и отшествий“ в МТ – 2000. В ней по пройденному расстоянию S от 0 до 100 миль и курсу через 1° выбирают значения РШ и ОТШ. Курсы первой четверти (NE) выделены и напечатаны жирным шрифтом, а рядом даны три курса остальных четвертей, которым соответствуют синусы и косинусы первой четверти. Значения РШ и ОТШ даны в таблице до сотых долей мили и поэтому могут быть использованы с достаточной точностью для плавания в 10 и 100 раз больших чем S. Таблица даёт решение прямоугольного треугольника по гипотенузе (локсодромии) и прилежащему к ней углу (курсу судна - К) (рис.4.36). Проекции локсодромии на меридиан и параллель могут быть выражены в морских милях или экваториальных милях.

Таблица 2.20 МТ – 2000 “Разность долгот”, составленная по формуле РД = ОТШ secj, даёт или приближённое или точное значение РД, в зависимости от того с каким значением широты - средней (j_m) или промежуточной (j_п) входят в таблицу. Если в таблицу войти с точным значением j_п, то получат точное значение (для Земли - сферы) РД, если с приближённым значением j_m, то получат приближённое значение РД. В таблице даны результаты вычислений для ОТШ в 1,2....9 и100 миль и для широт от 0° до 90°.

Для получения РД двух пунктов для десятков и сотен миль отшествия надо просто перенести запятую, отделяющую целую часть от дробной в выбранных из таблицы значений.

Для учёта сфероидичности Земли в разности широт (РШэ) следует по средней широте выбрать из таблицы 2.19б МТ – 2000 коэффициент f и рассчитать РШэ по формуле

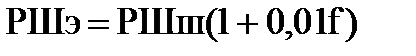, (4.80)

где РШш – разность широт для шара, выбранная из таблицы 2.19а МТ – 2000.

С учетом сфероидичности Земли РДэ может быть рассчитана по формуле

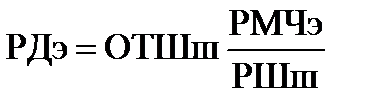, (4.81)

где РМЧэ – для земного эллипсоида, выбранная из таблицы 2.28а МТ – 2000, а РШш и ОТШш – для земного шара, выбранные из таблицы 2.19а.