Точность графического счисления
Возможные погрешности в элементах счисления, углах дрейфа и сноса, поправках компаса и лага, а также в графических построениях на карте, которые накапливаются, приводят к тому, что при ведении прокладки действительное место судна не совпадает с нанесённым на карту счислимым местом. Судоводитель должен уметь оценить точность графического счисления. Погрешности счисления разделим на две группы: погрешность в определении пути судна и погрешность в пройденном расстоянии. Погрешностями графических построений пренебрегаем ввиду их малости.
| |
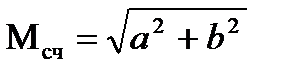 , называемым радиальной средней квадратической погрешностью счисления за время плавания по счислению.
, называемым радиальной средней квадратической погрешностью счисления за время плавания по счислению.
Значение величины b получим из DАВ1В:
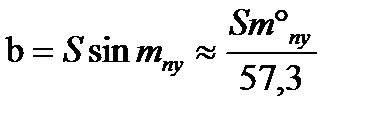 , (4.53)
, (4.53)
где mпу - средняя квадратическая погрешность суммарного путевого угла, град.
Величина а зависит от погрешностей в принятом значении поправки лага и от погрешностей в пройденном расстоянии, вызванных неучётом течения или учётом недостоверного течения.
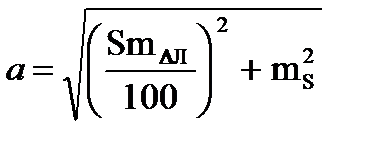 . (4.54)
. (4.54)
При отсутствии ветра и течения mпу = mк - средней квадратической погрешности курса, вызванной в основном погрешностью в поправке компаса.
Средняя квадратическая погрешность счисления при отсутствии внешнего воздействия (ветра и течения) зависит только от погрешностей в поправках лага и компаса:
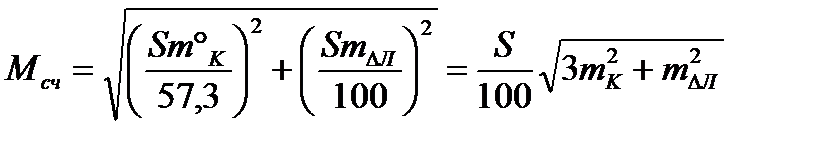 . (4.55)
. (4.55)
При учёте дрейфа в формуле (4.55) вместо mк будет 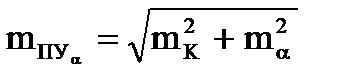 , где ma - средняя квадратическая погрешность в учёте угла дрейфа, которую можно принять
, где ma - средняя квадратическая погрешность в учёте угла дрейфа, которую можно принять 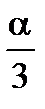 .
.
При наличии течения средняя квадратическая погрешность в учёте угла сноса от течения mb = f(V, mv, P, uт) и может достигать нескольких градусов. Целесообразно учитывать её максимальное значение.
Формулы для вычисления погрешностей mb и ms от действия течения могут быть получены из формул аналитического учёта течения
-
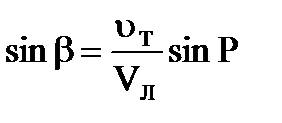 ,
, - V = Vл cosb + uт cos P.
Cчитая, что sin b » b arc1° и продифференцировав уравнение (1) по переменным uт и Р при Vл - cоnst, получим
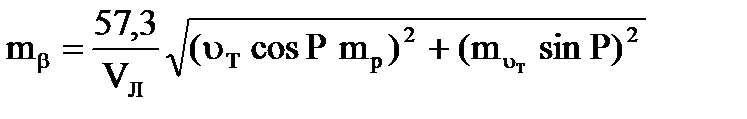 , (4.56)
, (4.56)
где mp- cкп направления течения, радианы, muт - скп в учёте скорости течения, узлы.
При Р = 90°
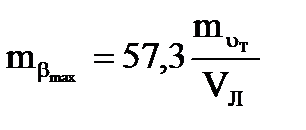 . (4.57)
. (4.57)
В уравнении (2), полагая b = 0°, после дифференцирования получим
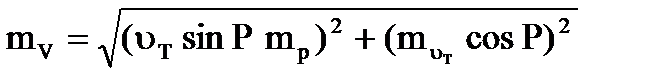 . (4.58)
. (4.58)
При Р = 0
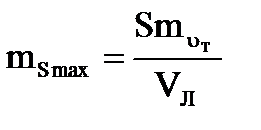 . (4.59)
. (4.59)
Среднее значение погрешности в скорости неизвестного течения принимается равным: 0,5 - 1,0 уз в районах со значительными приливо-отливными течениями; 0,3 - 0,5 уз в районах открытого моря, где по данным пособий течение отсутствует; 0,2 - 0,3 уз в прибрежной зоне; ветровое течение обычно не превышает 0,3 уз.
При совместном учёте дрейфа от ветра и сноса течением формула (4.53) после подстановки в неё выражения (4.56) примет вид
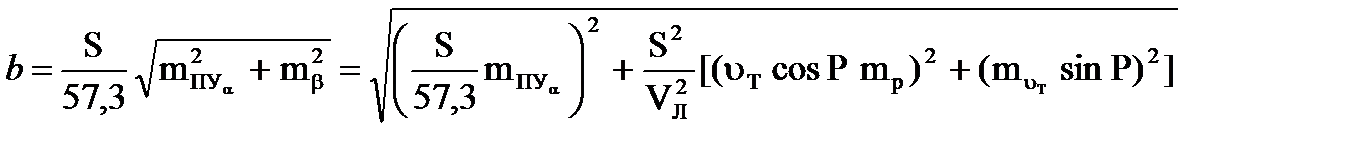 . (4.60)
. (4.60)
Если течение не учитывается (uт = 0), но оно может быть, то самый неблагоприятный случай будет при Р = 90°:
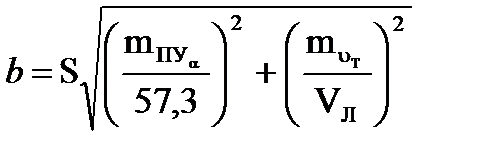 (4.61)
(4.61)
Формула (4.54) после подстановки ms = mv t примет вид
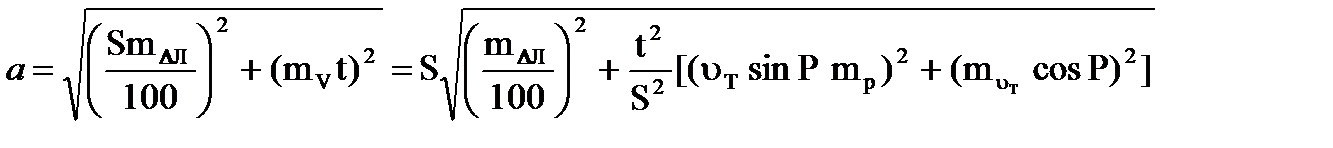 . (4.62)
. (4.62)
Если течение не учитывается, но оно может быть, то самый неблагоприятный случай будет при Р = 0°:
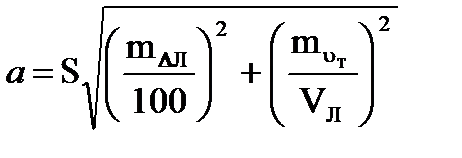 . (4.63)
. (4.63)
Приближённые значения скп счисления Мсч по многолетним наблюдениям для нормальных условий плавания в зависимости от пройденного расстояния: без ветра и течения Мсч = 0,02S, с учётом дрейфа Мсч = 0,03S; с учётом дрейфа и сноса течением Мсч = (0,03 - 0,07) S.
При плавании несколькими курсами скп счисления в конечной точке Мсч определяется по формуле (рис.4.34):
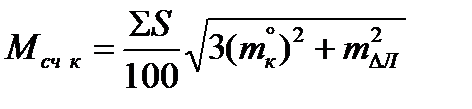 , (4.64)
, (4.64)
где Мсч к - средняя квадратическая погрешность счисления в конечной точке плавания по счислению; ΣS=S1+S2+…+Sn – сумма плавания по счислению на всех курсах.
Погрешность счисления можно рассчитать и статистическим методом. Экспериментально установлено, что средняя квадратическая погрешность счисления при интервалах счисления t £ 2 ч. изменяется по линейному закону
Мсч = 0,7 Ксч t, (4.65)
а при интервалах счисления t > 2ч - по параболическому закону
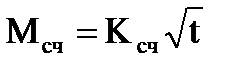 , (4.66)
, (4.66)
где Мсч - скп счисления в милях, t - интервал счисления в часах, Ксч- коэффициент точности счисления, зависящий от района плавания, степени изученности течений, гидрометеорологических условий плавания, типа судна, состава его технических средств судовождения и точности учёта элементов счисления. По формулам (4.65) и (4.66) составлена таблица 4.9а МТ – 2000.
Коэффициент точности счисления можно рассчитать, если при плавании по одному маршруту собрать данные о невязках между счислимыми и обсервованными местами. Обсервации должны быть равноточными и производиться через примерно равные интервалы времени. Для определения Ксч со скп 10% надо иметь не менее 50 невязок.
При интервале счисления t £ 2 ч коэффициент точности счисления рассчитывается по формуле
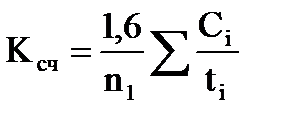 , (4.67)
, (4.67)
при t > 2 ч
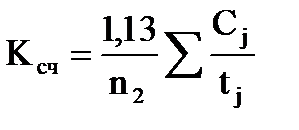 , (4.68)
, (4.68)
где Сi - невязки с интервалом ti £ 2 ч, а n1 - число таких невязок; Сj - невязки с интервалом tj > 2 ч, а n2 - число таких невязок.
Коэффициент точности счисления может быть предвычислен априорно по формуле
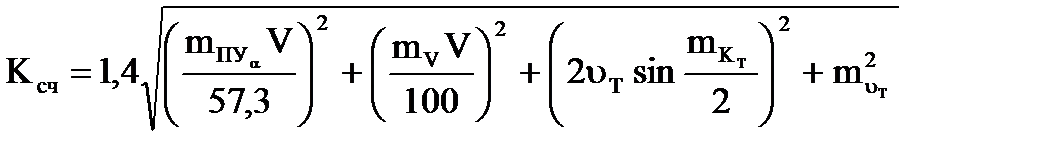 , (4.69)
, (4.69)
где 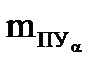 ,
, 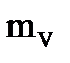 ,
, 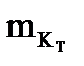 ,
, 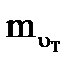 - предполагаемые средние квадратические погрешности в пути судна, его скорости и элементах течения.
- предполагаемые средние квадратические погрешности в пути судна, его скорости и элементах течения.
Если счисление велось от обсервованной точки, то средняя квадратическая погрешность счислимого места (Мc) определяется как квадратичное суммирование средней квадратической погрешности исходной обсервации (Мо) и средней квадратической погрешности счисления в конечной точке после обсервации
(Мcч к=Мсч 0-n)
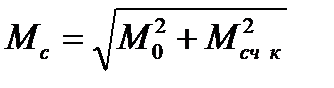 . , (4.70)
. , (4.70)
где Мсч к рассчитывается по формулам 4.64, 4.65, 4.66
По формуле (4.70) составлена таблица 4.9б МТ – 2000. СКП Мcч и Мc можно также определить по номограммам 4.10.1 и 4.10.2.
Если после длительного перехода нет возможности получить надёжную обсервацию, а необходимо пройти какой-либо пролив, подойдя к нему только по счислению, надо проложить линию курса из счислимой точки D и две линии параллельные линии курса из двух точек окружности радиуса Мк (рис.4.34). Такая прокладка называется тройной. Для получения предельных погрешностей с вероятностями Р = 95% и Р = 99% следует радиус Мс увеличить соответственно в 2 и 3 раза. Решение вопроса о возможности прохода узкости в отсутствии надёжной обсервации должно определяться свободным прохождением узкости полосой площади вероятного места судна.
 Рис. 4.34. Погрешность счисления при плавании несколькими курсами (Мсч-к), погрешность счислимого места в конечной точке (Мс) и тройная прокладка Рис. 4.34. Погрешность счисления при плавании несколькими курсами (Мсч-к), погрешность счислимого места в конечной точке (Мс) и тройная прокладка
|
Дата добавления: 2015-06-22; просмотров: 2409;
