Динамические ошибки в САУ. Способы нахождения коэффицентов динамических ошибок.

Динамическими называются ошибки в замкнутой системе при входном воздействии вида

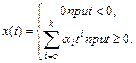
Этот сигнал относится к медленно меняющимся сигналам, так как (k+1) - ая производная этого сигнала по времени равна нулю.

Гармонический сигнал 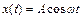не является медленно меняющимся, так как ни одна из его производных не равна нулю.

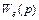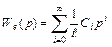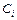Для определения динамической ошибки представим функцию рядом Тейлора , где - неизвестные коэффициенты ошибки. Тогда 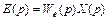= 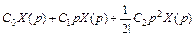+...+ 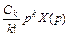(1).

Этот ряд ограничен k-тым членом ряда, так как 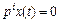при 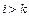, поэтому 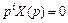при .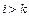

Взяв от (1) обратное преобразование Лапласа, получим 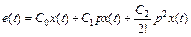+...+ 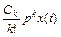(2), где 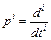- символ дифференцирования.

В ряде (2) первое слагаемое 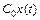называется ошибкой по положению, второе слагаемое 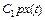называется ошибкой по скорости, а третье слагаемое 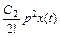называется ошибкой по ускорению.

Коэффициенты 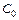, 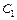и 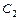называются соответственно коэффициентами ошибки по положению, скорости и ускорению. Слагаемые более высокого порядка и входящие в них коэффициенты ошибок 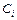специального названия не имеют.

Для определения коэффициентов ошибок C_i существует несколько способов.

Первый способ: коэффициенты ошибки C_i определяются по формуле

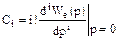, где 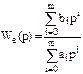- передаточная функция ошибки в виде дробно-рациональной функции. По этой формуле легко найти коэффициенты C_i для малого индекса i. В частности для i=0 имеем .

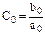Второй способ.

Имеем два выражения передаточной функции ошибки в виде отношения полиномов:

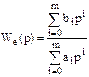
и виде усеченного ряда Тейлора 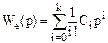. Приравняем правые части этих выражений и получим

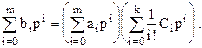
Раскроем скобки и приравняем коэффициенты при одинаковых степенях p, в результате получим

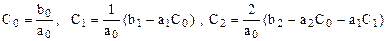и т.д.

Третий способ.

Имеем два выражения для передаточной функции ошибки: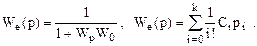

Представим произведение W_pW₀ в виде ,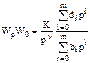

где K - коэффициент усиления замкнутой петли, n - порядок астатизма, равный числу интеграторов в петле.

Тогда .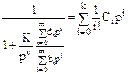

Далее как и во втором способе при различных порядках астатизма n делаем операции с раскрытием скобок и приравниванием коэффициентов при равных степенях p .

В результате получим.

При n=0 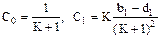и т.д.

При n=1 C₀=0 , 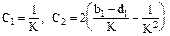и т.д.

При n=2 C₀=0 , С₁=0 , 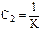и т.д.

Из этих выражений следует, что чем выше порядок астатизма замкнутой системы, тем больше коэффициентов системы равны нулю. Но в замкнутых системах с n>2 возникает проблема устойчивости.