Вектор ускорения точки

Ускорением точки называется векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки.

Пусть в некоторый момент времени 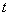движущаяся точка находится в положении М и имеет скорость 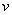, а в момент 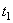приходит в положение 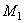и имеет скорость 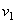(рис. 6).

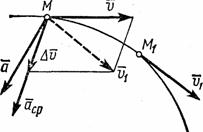
Рис.6

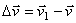Тогда за промежуток времени скорость точки получает приращение . Для построения вектора отложим от точки М вектор, равный 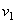, и построим параллелограмм, в котором диагональю будет 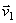, a одной из сторон 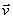. Тогда, очевидно, вторая сторона и будет изображать вектор . Заметим, что вектор всегда направлен в сторону вог­нутости траектории.

Отношение приращения вектора скорости к соответствующему про­межутку времени 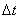определяет век­тор среднего ускорения точки за этот промежуток времени:

.

Вектор среднего ускорения имеет то же направление, что и век­тор , т. е. направлен в сторону вогнутости траектории.

Ускорением точки в данный момент времени t называется век­торная величина 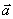, к которой стремится среднее ускорение при стремлении промежутка времени 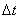к нулю: Вектор ускорения точки в данный момент време­ни равен первой производной от вектора скорости или второй произ­водной от радиуса-вектора точки по времени.

Найдем, как располагается вектор 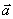по отношению к траекто­рии точки. При прямолинейном движении вектор 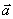направлен вдоль прямой, по которой движется точка. Если траекторией точки явля­ется плоская кривая, то вектор ускорения 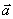, так же как и вектор , лежит в плоскости этой кривой и направлен в сторону ее вогнутости. Если траектория не является плоской кривой, то вектор на­правлен в сторону вогнутости траектории и лежит в плоскости, про­ходящей через касательную к траектории в точке М и прямую, па­раллельную касательной в соседней точке M₁ (рис. 4). В пределе, когда точка М стремится к М, эта плоскость занимает положение так называемой соприкасающейся плоскости, т.е. плоскости, в которой происходит бесконечно малый поворот касательной к траектории при элементарном перемещении движущейся точки. Следовательно, в общем случае вектор ускорения 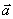лежит в соприкасающейся плоскости и направлен в сторону вогнутости кривой.