Определение ускорения при координатном способе задания движения

Вектор ускорения точки 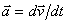в проекции на оси получаем:

, ,

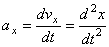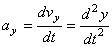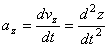
или

, , ,

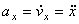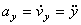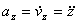т.е. проекция ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени. Модуль и направление ускорения найдутся из формул

;

, , ,

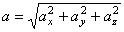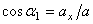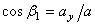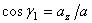где 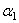, , 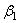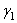- углы, образуемые вектором ускорения с координатными осями.

Пример 3. Движение точки задано уравнениями .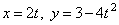

Из первого уравнения 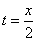. Подставив во второе, получим уравнение траектории: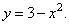

Это уравнение параболы. В на­чале движения, при 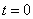, точка находи­лась на самом верху, в положении M₀ ( ).

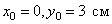А, например, при t =0,5 c она будет в положении M с координатами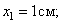

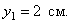
Проекции скорости на оси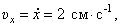

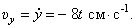
При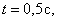

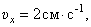
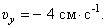
И модуль скорости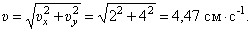

Составляющие скорости по осям и вектор её показаны в масштабе на рис. 7.

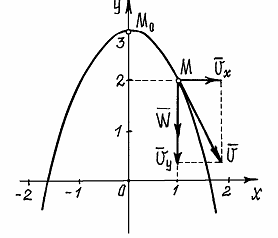
Рис.7

Проекции ускорения 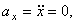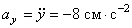. Так как проекция вектора ускорения на ось x равна нулю, а на ось y – отрица­тельна, то вектор ускорения на­правлен верти­кально вниз, и величина его постоянна, не за­висит от времени.