Некоторые частные случаи движения точки.

Пользуясь полученными результатами, рассмотрим некоторые частные случаи движения точки.

1) Прямолинейное движение. Если траекторией точки является прямая линия, то 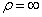. Тогда 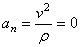и все уско­рение точки равно одному только касательному ускорению:

.

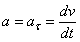Так как в данном случае скорость изменяется только численно, то отсюда заключаем, что касательное ускорение характеризует изменение скорости по численной величине.

2) Равномерное криволинейное движение. Равно­мерным называется такое криволинейное движение точки, в котором численная величина скорости все время остается постоянной: .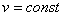

Тогда 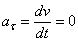и все ускорение точки равно одному только нормальному:

.

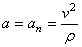Вектор ускорения 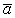направлен при этом все время по нормали к траектории точки.

Так как в данном случае ускорение появляется только за счет изменения направления скорости, то отсюда заключаем, что нормаль­ное ускорение характеризует изменение скорости по направ­лению. Найдем закон равномерного криволинейного движения.

Из формулы 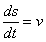имеем .

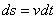Пусть в начальный момент ( 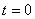) точка находится от начала отсчета на расстоянии 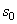. Тогда, беря от левой и правой части равенства определенные интегралы в соответствующих пределах, получим

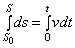или ,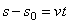

так как 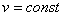. Окончательно находим закон равномерного криволинейного движения в виде

.

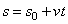Если 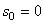, то s даст путь, пройденный точкой за время t. Следовательно, при равномерном движении путь, пройденный точкой, расчет пропорционального времени, а скорость движения равна отношению пути ко времени

.

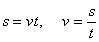3) Равномерное прямолинейное движение. В этом случае 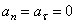, а значит и 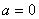. Заметим, что единственным движением, в котором ускорение точки все время равно нулю, является равномерное прямолинейное движение.

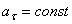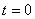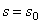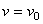4) Равнопеременное криволинейное движение. Равнопеременным называется такое криволинейное движение точки, при котором касательное ускорение остается все время величиною постоянной: . Найдем закон этого движения, считая, что при : , а , где 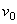- начальная скорость точки. Согласно формуле 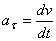имеем .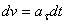

Так как 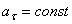, то, беря от обеих частей последнего равенства интегралы в соответствующих пределах, получим:

.

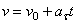Формулу представим в виде

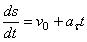или .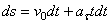

Вторично интегрируя, найдем закон равнопеременного криволинейного движения точки в виде

.

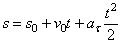Если при криволинейном движении точки модуль скорости возрастает, то движение называется ускоренным, а если убывает - замедленным.

Пример 4. Точка движется по окружности радиуса 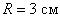по закону 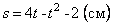. При 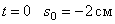. Значит, движение началось из M₀ (рис.10).

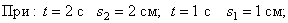
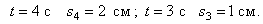
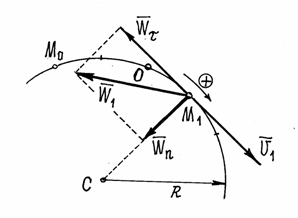
Рис.10

Судя по этим результатам, точка сначала двигалась в положительном направлении, а затем пошла обратно. В крайнем положении скорость точки станет равной нулю.

Так как 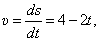то положив 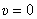, найдём время 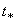когда точка окажется в этом крайнем положении: 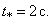Значит 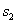определяет это положение точки.

Найдём скорость и ускорение точки при 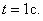Скорость 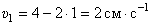. Направлен вектор скорости в положительном на­правлении ( ).

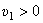Касательное ускорение 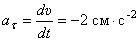. Вектор 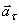направлен в отрицательном направлении. Нормальное ускорение 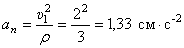(радиус кривизны дуги окружности равен её радиусу 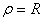). Полное ускорение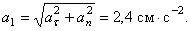

Так как вектор скорости 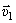и вектор касательного ускорения 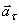направлены в противоположные стороны, точка в этот момент движется замедленно.