Определение скорости точки при координатном способе задания движения
Вектор скорости точки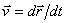 
, учитывая, что 
, 
, 
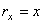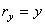, найдем:
, 
, 
.
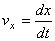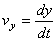Таким образом, проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.
Зная проекции скорости, найдем ее модуль и направление (т.е. углы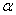 
, 
, 
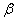, которые вектор 
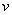образует с координатными осями) по формулам
;
, 
, 
.
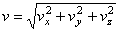Итак, численная величина скорости точки в данный момент времени равна первой производной от расстояния (криволинейной координаты) s точки по времени.
Направлен вектор скорости по касательной к траектории, которая нам наперед известна.
Дата добавления: 2015-06-17; просмотров: 760;