Кинематика точки. Введение в кинематику.

Лекция 1. Кинематика точки и твердого тела.

В данной лекции рассматриваются следующие вопросы:

1. Кинематика точки. Введение в кинематику.

2. Способы задания движения точки.

3. Вектор скорости точки.

4. Вектор ускорения точки.

5. Определение скорости и ускорения точки при координатном способе задания движения точки.

6. Определение скорости и ускорения точки при естественном способе задания движения точки. Касательное и нормальное ускорение точки.

7. Некоторые частные случаи движения точки.

Изучение данных вопросов необходимо в дальнейшем для динамики движения материальной точки, динамики относительного движения точки, динамики вращательного движения точки, для решения задач в дисциплинах «Теория машин и механизмов» и «Детали машин».

Кинематика точки. Введение в кинематику.

Кинематикой называется раздел механики, в котором изучаются геометрические свойства движения тел без учета их инертности (массы) и действующих на них сил.

Под движением мы понимаем в механике изменение, с течением времени положения данного тела в пространстве по отношению к другим телам.

Для определения положения движущегося тела (или точки) в разные моменты времени с телом, по отношению к которому изучается движение, жестко связывают какую-нибудь систему координат, образующую вместе с этим телом систему отсчета.

Изображать систему отсчета будем в виде трех координатных осей (не показывая тело, с которым они связаны).

Движение тел совершается в пространстве с течением времени. Пространство в механике мы рассматриваем, как трехмерное евклидово пространство.

Время является скалярной, непрерывно изменяющейся величиной. В задачах кинематики время 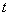принимают за независимое переменное (аргумент). Все другие переменные величины (расстояния, скорости и т. д.) рассматриваются как изменяющиеся с течением времени, т, е. как функции времени .

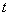Для решения задач кинематики надо, чтобы изучаемое движение было как-то задано (описано).

Кинематически задать движение или закон движения тела (точки) - значит задать положение этого тела (точки) относительно данной системы отсчета в любой момент времени.

Основная задача кинематики точки и твердого тела состоит в том, чтобы, зная закон движения точки (тела), установить методы определения всех кинематических величин, характеризующих дан­ное движение.

Способы задания движения точки

Для задания движения точки можно применять один из следую­щих трех способов:

1) векторный, 2) координатный, 3) естественный.

1. Векторный способ задания движения точки.

Пусть точка М движется по отношению к некоторой си­стеме отсчета Oxyz. Положение этой точки в любой момент времени можно определить, задав ее радиус-вектор 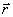, проведенный из на­чала координат О в точку М (рис. 1).

Рис.1

При движении точки М вектор 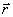будет с течением времени изме­няться и по модулю, и по направлению. Следовательно, 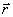является переменным вектором (вектором-функцией), зависящим от аргу­мента :

.

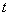Равенство определяет закон движения точки в векторной форме, так как оно позволяет в любой момент времени построить соответствующий вектор 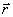и найти положение движущейся точки.

Геометрическое место концов вектора 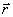, т.е. годограф этого вектора, определяет траекторию движущейся точки.

2. Координатный способ задания движе­ния точки.

Положение точки можно непосредственно опре­делять ее декартовыми координатами х, у, z (рис.1), которые при движении точки будут с течением времени изменяться. Чтобы знать закон дви­жения точки, т.е. ее положение в пространстве в любой момент вре­мени, надо знать значения координат точки для каждого момента времени, т. е. знать зависимости

, , .

Уравнения представляют собой уравнения движения точки в прямоугольных декартовых координатах. Они определяют закон движения точки при координатном способе задания движения.

Чтобы получить уравнение траектории надо из уравнений движения исключить параметр .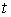

Нетрудно установить зависимость между векторным и координатным способами задания движения.

Разложим вектор 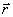на составляющие по осям координат:

где 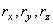- проекции вектора на оси; 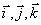– единичные векторы направленные по осям, орты осей.

Так как начало 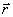вектора находится в начале координат, то проекции вектора будут равны координатам точки M. Поэтому

Пример 1.Движение точки задано уравнениями

Рис.2

Чтобы исключить время, параметр t, найдём из первого уравнения из второго Затем возведём в квадрат и сложим. Так как 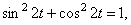получим Это уравнение эллипса с полуосями 2 см и 3 см (рис.2).

Начальное положение точки M₀ (при t=0) определяется координатами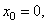

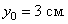
Через 1 сек. точка будет в положении M₁ с координатами

Примечание.

Движение точки может быть задано с помощью и других координат. Например, цилиндрических или сферических. Среди них будут не только линейные размеры, но и углы. При необходимости, с заданием движения цилиндрическими и сферическими координатами можно познакомиться по учебникам.

3. Естественный способ задания движе­ния точки.

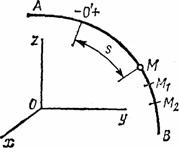
Рис.3

Естественным способом задания движения удобно пользоваться в тех слу­чаях, когда траектория движущейся точки известна заранее. Пусть кривая АВ явля­ется траекторией точки М при ее движении относительно системы отсчета Oxyz (рис.3) Выберем на этой траектории какую-нибудь неподвижную точку О', которую примем за начало отсчета, и установим на траектории положительное и отрицатель­ное направления отсчета (как на координат­ной оси).

Тогда положение точки М на тра­ектории будет однозначно определяться криволинейной коорди­натой s, которая равна расстоянию от точки О' до точки М, изме­ренному вдоль дуги траектории и взятому с соответствующим знаком. При движении точка М перемещается в положения M₁, М₂,... . следовательно, расстояние s будет с течением времени изменяться.

Чтобы знать положение точки М на траектории в любой момент времени, надо знать зависимость

.

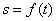Уравнение выражает закон движения точки М вдоль тра­ектории.

Пример 2. Точка движется по прямой линии, по закону (рис. 4).

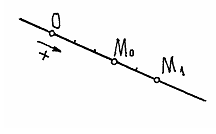
Рис.4

В начале движения, при 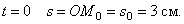Положение точки M₀ назы­вается начальным положением. При

Конечно, за 1 сек. точка прошла расстоя­ние M₀M₁=2см.Так что s – это не путь пройденный точ­кой, а расстояние от начала отсчёта до точки.