Вектор скорости точки

Одной из основных кинематических характеристик движе­ния точки является векторная величина, называемая скоростью точки.

Известно, что при движении точки по прямой линии с постоянной скоростью, равномерно, скорость её определяется делением пройденного расстояния s на время: . При неравномерном движении эта формула не годится. Введем сначала понятие о средней скорости точки за какой-нибудь промежуток времени. Пусть движущаяся точка находится

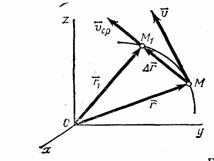
Рис. 5

в момент времени t в положении М, определяемом радиусом-векто­ром 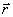, а в момент 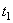приходит в положение M₁ определяемое векто­ром 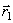(рис.5). Тогда перемещение точки за промежуток времени определяется вектором 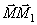который будем называть вектором перемещения точки. Из треугольника ОММ₁ видно, что 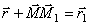; следовательно, .

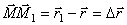Отношение вектора перемещения точки к соответствующему промежутку времени дает векторную величину, называемую сред­ней по модулю и направлению скоростью точки за промежуток времени :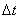

.

Скоростью точки в данный момент времени 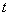называется векторная величина 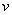, к которой стремится средняя скорость 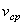при стремлении промежутка времени 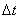к нулю:

, .

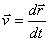Итак, вектор скорости точки в данный момент времени равен первой производной от радиуса-вектора точки по времени.

Так как предельным направлением секущей ММ₁ является касательная, то вектор скорости точки в данный момент времени направлен по касательной к траектории точки в сторону движения.