Поняття про ентропію. Властивості ентропії

Вище були одержані вирази для ККД реальної (6.59) і ідеальної (6.62) теплової машини. Ясно, що ККД реальної машини не більший, ніж ідеальної, тобто маємо нерівність 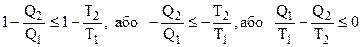. (6.63)

Відношення кількості теплоти Q до абсолютної температури Т джерела тепла називається приведеною кількістю теплоти. Враховуючи, що тепло Q₂ віддається, тобто Q₂ < 0, в лівій частині нерівності (6.63) стоїть алгебраїчна сума приведених кількостей теплот циклу, яка, як видно із (6.63), не боже бути позитивною. Вираз (6.63) можна переписати в інтегральній формі

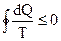. (6.64)

Це співвідношення називається нерівністю Клаузіуса і являється математичним записом другого начала термодинаміки.

Розглянемо деякий оборотний цикл (рис.6.32), який складається із двох процесів: 1а2 і 2б1. Для оборотного циклу у виразі (6.64) буде знак рівності. Одержимо

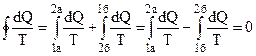. (6.65)

Тут враховано оборотність процесу 2б1, тобто .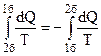

Рівняння (6.65) показує, що приведена кількість теплоти, одержана системою, не залежить від шляху переходу, а визначається тільки параметрами початкового (1) і кінцевого (2) станів. Цей факт дає можливість ввести певну функцію стану системи, ентропію S, зміна якої

дорівнює алгебраїчній сумі приведених кількостей теплот, тобто

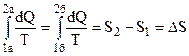. (6.66)

Якщо в циклі є необоротний процес 1н2 (рис.6.33), то

.

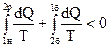
Так як для оборотного процесу (2б1) 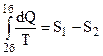, одержуємо 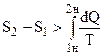, або в загальному випадку

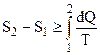(6.67)

Знак (=) для оборотного знак (>) для необоротного процесу. Для нескінченно малих величин маємо для зміни ентропії

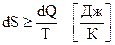. (6.68)

Які ж властивості ентропії та який її фізичний зміст?

– Ентропія функція стану системи;

– Ентропія величина адитивна. Це означає, що зміна ентропії системи дорівнює алгебраїчній сумі змін ентропії частин системи. Або загальна зміна ентропії в якомусь складному процесі дорівнює алгебраїчній сумі змін ентропії в простих процесах, із яких складається даний процес.

– Для теплоізольованої системи, тобто при адіабатних процесах, коли dQ = 0, із (6.68) випливає, що dS ≥ 0. Ентропія ізольованих систем не може зменшуватись, тобто процеси в таких системах ідуть тільки в напрямку збільшення ентропії. Це дає можливість теоретично прогнозувати протікання різних процесів. Якщо ентропія кінцевого стану більша, ніж початкового, процес може іти без зовнішнього втручання, наприклад, перехід тепла від гарячих до холодних частин системи. Не слід вважати, що ентропія взагалі не може зменшитись. Може, але для цього необхідно виконати певну роботу, тобто система вже буде незамкнутою.

– Нульовий рівень ентропії задається теоремою Нернста (німецький фізик і хімік), який у 1906 р встановив закон, який називають третім началом термодинаміки

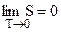. (6.69)

Ентропія системи при зменшенні її абсолютної температури до нуля теж зменшується до нуля.

– З’ясуємо фізичний зміст ентропії. З першого начала термодинаміки 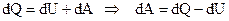. Нехай маємо ізотермічний оборотний процес. Тоді ,

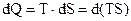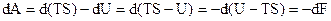. (6.70)

Тут 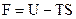називається вільною енергією – це та частина внутрішньої енергії, за рахунок зменшення якої (знак мінус в 6.70) система може виконати роботу. Тоді добуток TS дає ту частину внутрішньої енергії, яка не може перетворитись в роботу, тобто зв’язану енергію. Дійсно, якби в роботу можна було перетворити всю внутрішню енергію, це означало б зникнення системи.

– У 1872 р. австрійський фізик-теоретик Л.Больцман (1844-1906) зв’язав ентропію з термодинамічною ймовірністю W стану системи

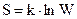. (6.71)

Тут k – стала Больцмана, W - термодинамічна ймовірність – це кількість мікроскопічних станів систем, якими може бути реалізований макроскопічний її стан. Наприклад, макроскопічний стан системи із трьох молекул газу – одна молекула знаходиться в одній половині посудини, а дві в другій може бути реалізований трьома способами (рис.6.34). Стани, зображені один під одним однакові, так як не уточнюється в якій саме (лівій чи правій) знаходиться одна молекула. Отже W = 3.