Принцип реактивного руху. Рівняння І.В.Мещерського і К.Е.Ціолковського

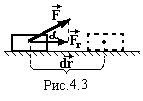
В основі реактивного руху лежить закон збереження імпульсу. Від тіла з певною швидкістю відокремлюється деяка маса. У відповідності із законом збереження імпульсу, швидкість руху тіла теж буде змінюватись, тобто це рух тіла змінної маси. Типовим прикладом ре­активного руху є рух ракети. Продукти згорання палива викидаються через сопло ракети, тоді її корпус рухається в протилежному напрямку (рис.4.3).

Знайдемо рівняння, яке описує рух ракети, та швидкість її руху. Введемо позначення:

m – маса ракети в момент часу t;

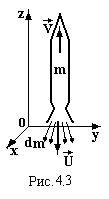
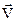- миттєва швидкість корпусу ракети відносно вибраної системи координат x,y,z;

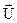- швидкість продуктів згорання палива віднос-но цієї ж системи координат x,y,z;

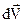- зміна швидкості корпусу ракети;

dm – маса викинутих за час dt продуктів згорання;

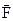- рівнодіюча зовнішніх сил.

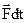Запишемо другий закон Ньютона: імпульс сили дорівнює зміні імпульсу системи „ракета-продукти згорання”

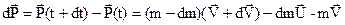
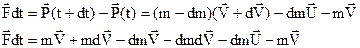
Нехтуючи доданком 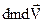, який набагато менший, ніж інші, так як є добуток двох нескінченно малих величин, одержуємо

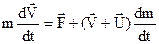. Векторна сума 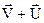дає швидкість 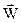витоку газів відносно корпусу ракети. Її величина залишається незмінною, так як вона визначається конструкцією сопла реактивного двигуна. Рівняння 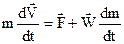(4.5)

називається рівнянням І.В.Мещерського (російський вчений, 1859-1935). Другий доданок в рівнянні (4.5) має розмірність сили і називається реактивною силою, яка виникає за рахунок зміни маси тіла з часом .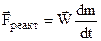

К.Е.Ціолковський (російський вчений, 1857-1935) розв’язав рівняння (4.5) Мещерського для випадку відсутності зовнішніх сил 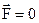з початковими умовами: при t = 0 V = 0, m = m_o –стартова маса ракети. В скалярній формі рівняння (4.5) в проекції на вертикальну вісь z має вид 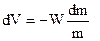. Інтегрування дає 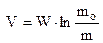. (4.6)

Це рівняння К.Е.Ціолковського. Воно показує, що кінцева швидкість ракети пропорційна відносній швидкості витоку газів і тим більша, чим більше відношення стартової маси m_o до кінцевої маси m. Щоб збільшити це відношення, Ціолковський запропонував багатоступеневі реактивні двигуни. Конструктивно неможливо виготовити легкий корпус двигуна, заправивши в нього велику масу палива. Модульний же корпус дає можливість збільшити відношення m_o/m, а значить і кінцеву швидкість ракети.

4.3 Механічна робота. Потужність

Поняття механічної роботи пов’язане з переміщенням. Якщо під дією сили 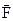тіло переміщується на відстань 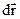(рис.4.4), то елементарна механічна робота

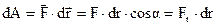(4.7)

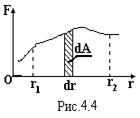дорівнює скалярному добутку сили на переміщення. На графіку залежності сили від переміщення (рис.4.5) вона відповідає площі заштрихованої області. Вся робота змінної сили знаходиться як інтеграл 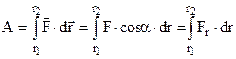(4.8)

і чисельно дорівнює площі, обмеженій лініями r₁, r₂, віссю Or абсцис і кривою F(r). Вимірюється робота в джоулях [A]=H∙м = Дж.

Потужність – це швидкість виконання роботи, тобто це робота, виконана за одиницю часу

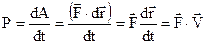(4.9)

і дорівнює скалярному добутку сили і швидкості. Потужність вимірюється у ватах [P] = Дж/с = вт. Позасистемною одиницею потужності є кінська сила 1к.с. = 735 вт.