Зв’язок між напруженістю і потенціалом

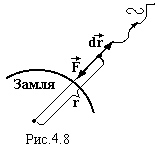
Силове поле, в якому робота не залежить від форми шляху, а визначається тільки положенням початкового і кінцевого положення тіла, називається потенціальним. Прикладом потенціального поля є гравітаційне поле, електростатичне поле. Такі поля характеризуються окрім силової векторної характеристики – напруженості ще й скалярною, енергетичною характеристикою – потенціалом.

Потенціалом гравітаційного поля називається робота, яку виконують гравітаційні сили по переміщенню тіла одиничної маси із даної точки поля в нескінченність, де поле уже відсутнє (рис.4.9).

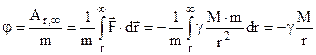
Одержали, що потенціал гравітаційного поля Землі 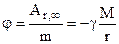(4.16)

залежить тільки від положення тіла, тобто радіус-вектора r.

Робота по переміщенню тіла m із точки 1 в точку 2 дорівнює

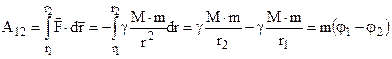(4.17)

добутку маси на різницю потенціалів. Одиницею вимірювання потенціалу є [φ]=Дж/кг=(м/с)².

Знайдемо зв’язок між напруженістю і потенціалом. За означенням потенціалу (4.16) і напруженості (див.розд.3.8) маємо

,

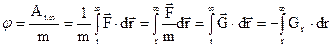де G_r – проекція вектора напруженості 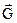на напрямок 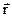. Взявши похідну з останнього виразу по радіус-вектору r, одержуємо

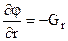, або в декартовій системі координат

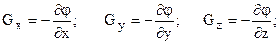. Тоді вектор напруженості запишеться через одиничні вектори (орти)

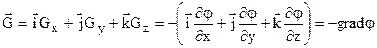. (4.18)

Векторна функція 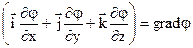називається градієнтом скалярної величини φ і дає швидкість її зміни з координатою. Напрямок вектора градієнта вказує напрямок найбільш швидкого зростання функції φ з координатою.

Помноживши (4.18) на масу m, одержимо зв’язок між силою і потенціальною енергією

. (4.19)