Застосування законів збереження імпульсу і енергії до центрального удару куль

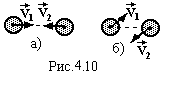Ударом називається явище кінцевої зміни швидкостей тіл за відносно короткий проміжок часу їх взаємодії між собою. Розрізняють центральні і косі удари. При центральному ударі вектори швидкостей співпадають за напрямком з лінією, що з’єднує центри мас тіл (рис.4.11,а). При косих ударах вектори швидкостей утворюють з цією лінією кут, відмінний від нуля (рис.4.11,б). Ми будемо розглядати центральний удар. Які ж процеси відбуваються при ударі? Кінетична енергія тіл в момент удару частково, або повністю перетворюється в потенціальну енергію деформації, яка потім, в залежності від характеру деформації, повністю, або частково знову перетворюється в кінетичну енергію і в тепло (тіла нагріваються за рахунок деформації).

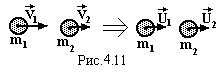Розглянемо центральний удар двох куль, які рухаються горизонтально, що дає можливість не враховувати зміну потенціальної енергії в полі тяжіння Землі. Запишемо закон збереження імпульсу (4.20) і закон збереження енергії (4.21) з врахуванням теплоти Q, яке виділяється при ударі

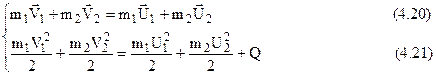
Маємо систему двох рівнянь з трьома невідомими: U₁, U₂, Q. В загальному випадку вона не має розв’язку. Тому цю задачу розв’язують для двох ідеальних випадків:

– абсолютно не пружний (пластичний) удар, після якого тіла рухаються як одне ціле. Тому можна записати третє рівняння

U₁ = U₂ = U (4.22)

–абсолютно пружній удар, при якому теплота не виділяється, тобто Q = 0 (4.23)

Абсолютно пластичний удар. Маємо систему рівнянь:

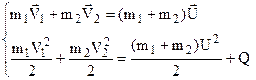(4.24)

звідки знаходимо

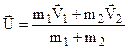
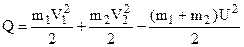. (4.25)

Розглянемо випадок, коли одне із тіл, наприклад, друге не рухається, тобто V₂ = 0. Одержуємо:

.

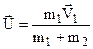
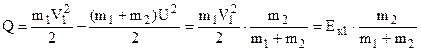– Коли m₂ >> m₁, тобто легким тілом m₁ ударяють по нерухомому масивному тілу m₂. Q = E_к1 – в енергію деформації перетворюється майже вся кінетична енергія тіла, яке ударяє, наприклад, ковка деталей.

– Коли m₂ << m₁. Важким тілом m₁ ударяють по легкому нерухомому тілу m₂.

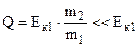- в енергію деформації перетворюється незначна доля енергії тіла, яке ударяє, тобто вся енергія перетворюється в кінетичну енергію, наприклад, пори забиванні цвяхів.

Абсолютно пружний удар. Маємо систему рівнянь:

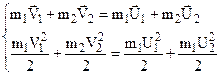. (4.26)

Знаходимо із цієї системи швидкості тіл U₁ і U₂ після удару. Перепишемо систему так:

.

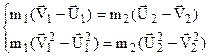Розкладемо у другому рівнянні різницю квадратів

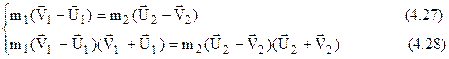Враховуючи (4.27) після скорочення (4,28) одержимо систему лінійних рівнянь

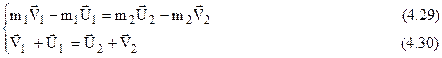
Помноживши (4.30) на m₂ і віднімаючи із (4.29), знаходимо 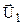. Помноживши (4.30) на m₁ і додаючи до (4.29), знаходимо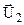

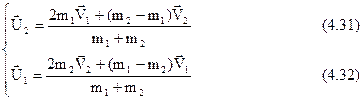
Розглянемо два випадки співвідношення мас:

а) m₁ = m₂ =m, тобто маси тіл однакові. У цьому випадку маємо

, тобто тіла „обмінюються” швидкостями;

б) m₂ >> m₁ – легке тіла m₁ ударяє по масивному m₂. Одержимо

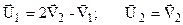. Швидкість масивного тіла m₂ не змінюється, а швидкість легкого тіла змінюється на подвоєну початкову швидкість масивного тіла. Якщо легке тіло m₁ наздоганяє масивне m₂, швидкість легкого тіла зменшується на подвоєну швидкість V₂ масивного. Якщо легке тіло m₁ рухається назустріч масивному m₂, то його швидкість збільшується на подвоєну швидкість V₂ масивного тіла.

Критерієм пружного чи пластичного удару є коефіцієнт відновлення k. Це відношення відносних швидкостей тіл до і після удару

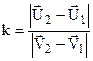. (4.33)

Для абсолютно пластичного удару k = 0, для абсолютно пружного k = 1.