Алгоритм расчета на устойчивость
Рассмотрим его на примере рамы (рис. 18.7 а).
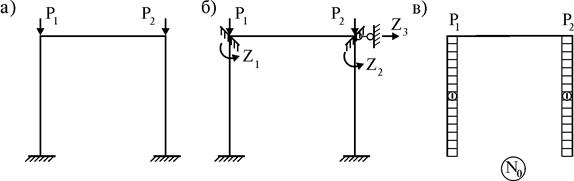
Рис. 18.7
1. Определение числа неизвестных: 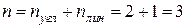 .
.
2. Выбор основной системы (рис. 18.7 б).
3. Построение эпюры продольных сил в основной системе (рис. 18.7 в).
4. Определение параметров устойчивости стержней
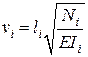 .
.
Желательно выразить все параметры устойчивости стержней через максимальный из них и принять v=max vi.
5. Запись канонических уравнений (в момент потери устойчивости все грузовые коэффициенты равняются нулю):
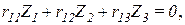
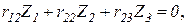
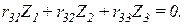
6. Запись уравнения устойчивости
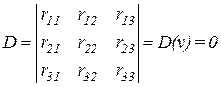 .
.
7. Рассмотрение единичных состояний (в этом примере – их три).
8. Построение единичных эпюр. Для этого используется специальная таблица метода перемещений, учитывающая влияние продольной силы на внутренние усилия стержня. Например, эпюра изгибающих моментов стержня с защемленными концами является криволинейной (рис. 18.8), а величины моментов определяются сложными функциями.
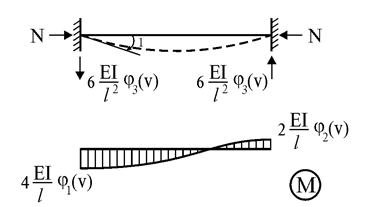
Рис. 18.8
К примеру, одна из этих функций определяется так:
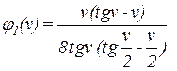 .
.
Ввиду сложности этих функций, они определяются по специальной таблице метода перемещений.
9. Определение коэффициентов канонических уравнений.
10. Решение уравнения устойчивости (вычисление ее критического корня 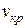 ).
).
11. Определение критической силы:
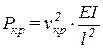 .
.
Дата добавления: 2015-06-17; просмотров: 1851;
