Показатели доходности и риска акций компании Макдоналдс
| Год | Доходность МД Rmd | Доходность рынка Rm | Отклонение МД (Rmd-Rcmd) | Отклонение рынка (Rm-Rcm) | Квадрат отклонения рынка (Rm-Rcm)2 | Произведение отклонений (Rmd-Rcmd)* (Rm-Rcm) |
| -0,0388 | -0,0392 | -0,1113 | -0,1153 | 0,0133 | 0,0128 | |
| -0,1019 | -0,0204 | -0,1744 | -0,0965 | 0,0093 | 0,0168 | |
| -0,0620 | 0,0729 | -0,1345 | -0,0032 | 0,0004 | ||
| 0,1238 | 0,1553 | 0,0513 | 0,0792 | 0,0063 | 0,0041 | |
| 0,3411 | 0,0756 | 0,2686 | -0,0005 | -0,0001 | ||
| -0,0765 | 0,0625 | -0,1490 | -0,1386 | 0,0192 | 0,0207 | |
| 0,1676 | 0.3416 | 0,0951 | 0,2655 | 0,0705 | 0,0252 | |
| -0,2677 | -0,3402 | -0,0761 | 0,0058 | 0,0259 | ||
| 0,5665 | 0,1615 | 0,4902 | 0,0854 | 0,0073 | 0,0422 | |
| Среднее | 0,0725 | 0,0761 | ||||
| Всего | 0,1317 | 0,1480 |
Ковариация доходности акций Макдоналдс и рынка будет равна
CV(Rmd, Rm) = 0,1480/9 = 0,0164.
Далее определяем дисперсию рынка.
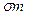2.= 0,1317/9 = 0,0146.
Бета коэффициент акций Макдоналдс найдем из следующего соотношения:
βi =CV(Rmd,Rm) / 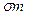2 = 0,0164/0,0146 = 1,123
Важным свойством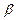 
-коэффициента является то, что 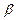портфеля вычисляется как взвешенная сумма 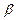- коэффициентов составляющих его активов. При этом следует помнить, что общий риск портфеля не является взвешенной суммой рисков составляющих его активов. Обусловлено это тем обстоятельством, что бета измеряет только систематический риск актива.
Исходя из вышесказанного для расчета 
-коэффициента портфеля акций может быть использовано следующее соотношение
p = 1*W1+ 2*W2+… + n*Wn,
Например, инвестор имеет 40 тыс. долл. и сформировал портфель из четырех акций, вложив в каждый вид акций по 10 тыс. долл. Если каждая акция имеет = 0,8, то бета такого портфеля также будет равен 0,8:
p = 0,8 х 0,25 + 0,8 х 0,25 + 0,8 х 0,25 = 0,8.
Такой портфель будет менее рисковым, чем весь рынок акций, и будет испытывать меньшее колебание доходности по сравнению со всем рынком. Теперь представим, что одна из акций продана и заменена акцией, имеющей = 2, тогда риск портфеля увеличится и его бета возрастет:
p = 0,8 х 0,25 + 0,8 х 0,25 + 0,8 х 0,25 + 2,0 х 0,25 =1,1.
Если одну из акций заменить на акцию с = 0,2, то бета портфеля снизится и составит:
p = 0,8 х 0,25 + 0,8 х 0,25 + 0,8 х 0,25 + 0,2 х 0,25 = 0,65.
Таким образом, риск портфеля может быть снижен путем включения в портфель акций, имеющих низкое значение -коэффициента.
В таблице 5.10 представлены -коэффициенты ряда компаний.
Рассмотренная модель оценки капитальных активов САРМ может быть использована для определения ставки дисконтирования при анализе эффективности инвестиций. Ставка дисконтирования в этом случае находится по формуле:
R = Rf + β * (Rm - Rf),
где R – ставка дисконтирования, Rf – безрисковая ставка, Rm – общая доходность рынка в целом, β – бета коэффициент, являющийся мерой рыночного риска для данных инвестиций. Коэффициент β может быть рассчитан с использованием рассмотренной выше методики. Кроме этого значения бета коэффициентов отраслей экономики публикуются специализированными изданиями, например, журналом «Рынок ценных бумаг».
Таблица 5.10
Дата добавления: 2015-06-17; просмотров: 647;