Показатели доходности и риска портфеля. Таким образом, заимствование по безрисковой ставке позволяет получить доходность портфеля выше, чем у рискового актива
| Удельный вес актива А, % | Доходность портфеля Rp, % | Бета портфеля |
| 0.0 | ||
| 0.4 | ||
| 0.8 | ||
| 1.2 | ||
| 1.6 | ||
| 2.0 | ||
| 2.4 |
Таким образом, заимствование по безрисковой ставке позволяет получить доходность портфеля выше, чем у рискового актива, что, естественно, приводит и к возрастанию систематического риска портфеля.
График зависимости доходности и бета портфеля представлен на рисунке 5.7. Наклон прямой определяется следующим выражением:
Наклон = S = (RА – Rf)/  А. = (20%-8%)/1,6 = 7,5%.
А. = (20%-8%)/1,6 = 7,5%.
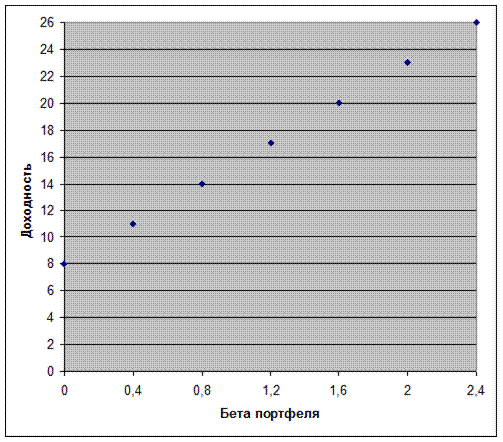
Рис. 5.7. Зависимость между доходностью портфеля и его коэффициентом бета
Данное соотношение характеризует доходность, приходящуюся на единицу систематического риска. В данном случае эта доходность составляет 7,5%.
Показатель доходности на единицу систематического риска может быть использован для сравнения инвестиционных свойств рисковых активов. Пусть, например, необходимо сравнить активы А и В показатели доходности и риска которых соответственно равны: RA = 20%,  А = 1,6; RВ = 16%,
А = 1,6; RВ = 16%,  В = 1,2. Необходимо выбрать актив, имеющий лучшие инвестиционные свойства. Рассчитаем показатели доходности на единицу риска для обоих активов:
В = 1,2. Необходимо выбрать актив, имеющий лучшие инвестиционные свойства. Рассчитаем показатели доходности на единицу риска для обоих активов:
SА = (RА – Rf)/  А. = (20%-8%)/1,6 = 7,5%.
А. = (20%-8%)/1,6 = 7,5%.
SВ = (RВ – Rf)/  В. = (16%-8%)/1,2 = 6,67%.
В. = (16%-8%)/1,2 = 6,67%.
Таким образом, актив А имеет большую доходность на единицу риска, чем актив В, что позволяет говорить об его лучших инвестиционных качествах.
Мы рассмотрели подход, позволяющий сравнить инвестиционные качества ценных бумаг по отношению к аналогичным бумагам. Большую значимость имеет сопоставление инвестиционных качеств бумаги по сравнению с рынком в целом. Это можно сделать с помощью выражения для линии рынка ценных бумаг (Security Market Line SML).
Ri = Rf + βi * (Rm - Rf),
Наклон данной прямой будет следующим
S = (Rm - Rf)/ βM = (Rm - Rf)/ 1 = Rm - Rf.
Показатель Rm – Rf называют премией рыночного риска. Данный показатель может быть использован для выявления недооцененных и переоцененных рынком акций. Пусть, например, для рассмотренного выше примера доходность рыночного портфеля составляет 15%. Премия за единицу рыночного риска в этих условиях будет равна
S = Rm – Rf. = 15% – 8% = 7%.
Таким образом, актив А обеспечивает большую доходность на единицу систематического риска, чем рыночный портфель, а актив В – меньшую. Такая ситуация в условиях эффективного рынка привела бы к тому, что цена на актив стала расти, доходность снижаться и приближаться к среднерыночной. Для актива В ситуация развивалась бы в противоположном направлении – цена стала понижаться, а доходность расти и приближаться к среднерыночной.
В данном примере актив А следует рассматривать в качестве недооцененного, т.е. его цена ниже справедливой рыночной цены, а актив В – переоцененного.
Дата добавления: 2015-06-17; просмотров: 613;
