Показатели риска активов
| Актив | Стандартное отклонение 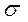
|  -коэффициент -коэффициент
|
| А | 0,8 | |
| В | 1,2 |
Необходимо определить:
1. Какой актив имеет больший полный риск?
2. Какой актив имеет больший рыночный риск?
3. Какой актив будет иметь большую премию за риск?
В качестве показателя полного риска выступает стандартное отклонение и, следовательно актив А будет иметь больший полный риск. При этом его рыночный риск меньше, чем у актива В. Так как полный риск складывается из систематического и несистематического рисков, то такая ситуация обусловлена наличием у актива А большого несистематического риска. Премию за риск будет иметь большую актив В, так как его рыночный риск выше.
Бета коэффициент акций или других ценных бумаг рассчитывается как отношение ковариации актива и рыночного портфеля и дисперсии рыночного портфеля:
βi = 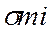 /
/ 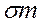 2.
2.
Числитель представляет вклад индивидуального актива I в величину риска диверсифицированного портфеля, а знаменатель – величину риска рыночного портфеля. Таким образом, бета измеряет систематический риск относительно риска рынка в целом.
Таким образом, величина βговорит о том, насколько систематический риск актива больше или меньше риска рыночного портфеля. Активы со значением β<1– менее рисковы, а с β>1 –более рисковы, чем рыночный портфель в целом.
Пример. Рассмотрим процедуру вычисления бета коэффициента на примере компании Макдоналдс (см. табл. 5.9). В колонках 2 и 3 представлены данные по годовой доходности за 9 лет для акций компании Макдоналдс и для рынка в целом. В колонках 4 и 5 представлены разности между текущей доходностью и средней доходностью. Так, например, значение -0,1113 в колонке 4 для 1977 года получается путем вычитания из доходности акций Макдоналдс в 1997 году равной -0,0388 среднего значения доходности равной 0,0725. В колонке 6 представлены квадраты отклонения ежегодной доходности рынка от среднего значения, а в колонке 7 – произведения ежегодных отклонений доходности акций Макдоналдс и рынка.
Таблица 5.9
Дата добавления: 2015-06-17; просмотров: 694;
