Число акций

Рис. 5.6. Влияние диверсификации на риск портфеля

Так, например, стандартное отклонение портфеля состоящего из одной акции будет равно примерно 28%. Средний портфель состоящий из двух случайно выбранных акций будет уже иметь стандартное отклонение примерно 25%, а из десяти – 18%. Процесс снижения риска по мере увеличения числа составляющих его активов представлен на рисунке. Портфель, состоящий из всех акций, принято называть рыночным. В данном примере он имеет стандартное отклонение равное 15%, которое и определяет рыночный риск.

Таким образом, общий риск, связанный с акциями складывается из специфического и систематического риска. При этом специфический риск может быть устранен посредством диверсификации. Известно, что доходность и риск актива связаны пропорциональной зависимостью. При этом ожидаемая доходность зависит только от систематического риска актива. Таким образом, вне зависимости от величины общего риска актива его ожидаемая доходность определяется только связанным с ним рыночным риском.

В качестве показателя систематического риска актива используется коэффициент бета ( 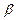-коэффициент). Он характеризующего степень изменчивости акции по отношению к «средней акции», которая двигается синхронно со всем рынком акций.

Это означает, что если доходность по рынку в целом увеличивается на 10%, то доходность «средней акции» возрастает в такой же степени, и, наоборот – при падении – падает. Портфель акций с 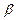-коэффициентом, равным единице, будет иметь такую же степень риска, как и весь рынок. Если для акции 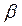= 0,5, это означает, что ее доходность будет повышаться или падать вдвое меньше, чем у всего рынка. Портфель акций с таким -коэффициентом будет иметь вдвое меньшую степень риска по сравнению с портфелем, имеющим =1. В то же время если акция имеет = 2, то ее подвижность вдвое выше, чем у средней акции. Нулевое значение бета соответствует отсутствию систематического риска, а бета равное единице – систематическому риску рыночного портфеля.

Таким образом, риск каждого актива складывается из систематического и несистематического риска. При этом в качестве показателя рыночного риска выступает -коэффициент.

Если известен показатель бета актива, то его доходность в рамках модели оценки капитальных активов CAPM (Capital asset pricing model) может быть определена из следующего соотношения:

R_i = R_f + β_i * (R_m - R_f),

Где R_i – ожидаемая доходность актива, R_m, R_f – доходность рыночного портфеля и безрисковая доходность, β_i – бета коэффициент актива. Данное уравнение называют линией рынка ценных бумаг (Security Market Line SML). Доходность актива в данном случае складывается из безрисковой доходности плюс премии за рыночный риск, присущий активу.

Таким образом, в соответствии с моделью САРМ доходность актива зависит от трех параметров:

1. Безрисковой доходности R_f, которая в основной определяется зависимостью стоимости денег от времени.

2. Величиной премии за рыночный риск, которая определяется соотношением (R_m - R_f).

3. Показателем рыночного риска конкретного актива β_i.

Пример. Имеется два актива А и В. Их показатели риска – стандартное отклонение и -коэффициент представлены в таблице 5.8.

Таблица 5.8