В режиме насыщения число электронов, вылетевших с катода, равно числу электронов, достигших анода. Ток эмиссии равен анодному току.

Как видно из анодной характеристики, увеличение анодного тока не прямо пропорционально изменению напряжения на аноде. Чем больше анодное напряжение, тем быстрее возрастает анодный ток. Этот закон нарушается лишь в режиме насыщения, поскольку все ресурсы для увеличения потока электронов на анод оказываются исчерпанными. Тогда только увеличение тока эмиссии (повышение напряжения накала) может вызвать повышение анодного тока.

Рассмотрим зависимость, связывающую анодный ток и анодное напряжение в диоде, образованном двумя плоскими, безграничными, параллельными, друг другу пластинами (рис. 8), для которых можно, пренебречь краевым эффектом и считать поле между анодом и катодом однородным. Примем следующие допущения.

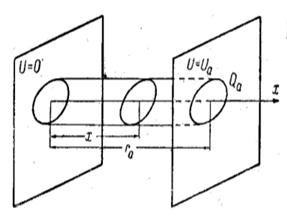
Рис. 8. К выводу закона степени 3/2.

Пусть на поверхности катода (x = 0) U = 0 и 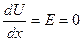начальная

скорость электронов 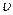₀ = 0 и потенциал анода U = U_а. Скорость электрона в каждой точке междуэлектродного пространства, если 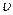₀ = 0, определяется выражением

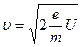. (12)

Учитывая, что в междуэлектродном пространстве существует пространственный заряд, воспользуемся уравнением Пуассона, которое при условии, что E_y = E_z = 0 и явления происходят в вакууме, можно записать в виде

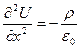. (13)

Здесь

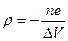(14)

— объемная плотность заряда.

Выражая элементарный объем ΔV через произведение элементарной площадки Δs на расстояние Δх, которое можно записать как произведение скорости электрона на время Δх = 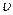Δt, получим:

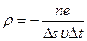. (15)

В этом выражении 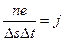- плотность тока.

Отсюда

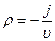, (16)

или с учетом (12) имеем:

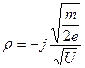. (17)

Подставляя выражение для 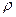в (13), запишем уравнение Пуассона в виде

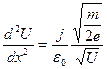. (18)

Умножая обе части равенства на 2 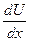и интегрируя от 0 до х, получим:

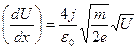. (19)

Постоянные интегрирования равны нулю, так как при x = 0 U = 0 и .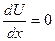

Интегрирование (19) после извлечения корня из обеих частей равенства и разделения переменных приводит к следующему результату:

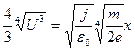. (20)

Отсюда легко определить плотность тока:

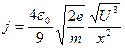. (21)

Плотность анодного тока можно найти, заменив х = r_а. Подставляя численные значения е и m, и выражая ток в амперах, а разность потенциалов в вольтах, получим:

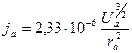, а/см². (22)

Чтобы найти величину анодного тока, умножим (22) на величину поверхности анода:

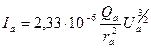, а, (23)

или

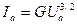, (24)

где

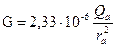(25)

— для данного типа лампы величина постоянная.

Выражение (23), отображающее аналитически функцию I_а = f(а), носит название закона степени трех вторых.

Согласно начальным условиям закон (23) получен для диода, образованного двумя плоскими электродами. При цилиндрической конструкции электродов в знаменатель правой части (23) следует ввести поправочный коэффициент β², зависимость которого от соотношения r_a/r_к представлена на рис. 9.

Величина Q_a, использованная при выводе, называет эффективной поверхностью анода. Для цилиндрической конструкции электродов она равна внутренней поверхности анода, так как катод обычно длиннее анода и электроны попадают на всю внутреннюю поверхность анода. Для плоских электродов эффективной поверхностью считают ту часть поверхности анода, на которую падают электроны.

Выражение (23), определяющее изменение анодного тока в зависимости от анодного напряжения в соответствии с полукубической параболой (степень 3/2), справедливо для режима пространственного заряда. В режиме насыщения, в идеальном случае, ток анода не должен зависеть от напряжения на аноде. Идеальные анодные характеристики диода, соответствующие аналитической зависимости, представлены на рис. 10.

Как видно из сравнения рис. 7,а и рис. 10, реальные анодные характеристики значительно отличаются от идеальных. Причина этого заключается в особенностях прохождения тока в диоде, не учтенных при выводе закона степени 3/2. Основные из этих особенностей следующие.

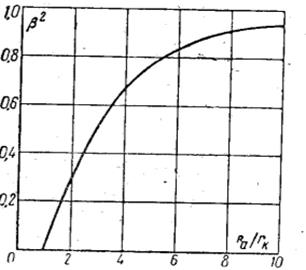
Рис. 9. График для определения величины коэффициента β².

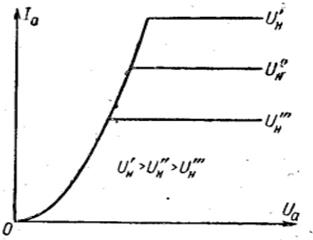
Рис. 10. Идеальные анодные характеристики диода.