Движение электронов в однородном электрическом поле

Предположим, что электрическое поле образовано плоским конденсатором, подключенным к батарее, с разностью потенциалов U. Размеры пластин конденсатора достаточно велики для того, чтобы пренебречь краевым эффектом и в рассматриваемом объеме считать электрическое поле однородным.

Как известно, электрон в однородном электрическом поле подвергается воздействию постоянной силы 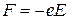. Согласно второму закону Ньютона эта сила равна:

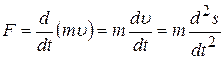. (1)

Отсюда общее уравнение движения электрона в электрическом поле имеет вид:

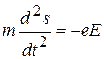. (2)

Это общее уравнение можно написать в виде проекций отрезка пути и вектора напряженности поля на оси координат:

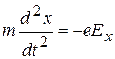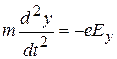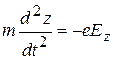, , . (З)

Расположим ось координат, как показано на рис. 1, и рассмотрим случай, когда электрон входит в однородное поле из качала координат (х = 0, y = 0, z = 0). Вектор его начальной скорости 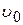лежит в плоскости хОz и составляет с положительной осью z угол q. Отсюда составляющие начальной скорости электрона по осям:

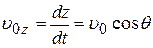и .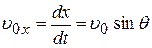

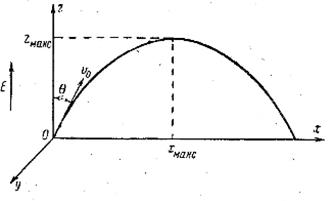
Рис. 1. Движение электрона в однородном электрическом поле.

Вектор напряженности поля параллелен оси z, и следовательно, Е_х = 0, E_у = 0, E_z = E. Электрон, очевидно, будет двигаться в плоскости xOz. Следовательно, уравнения движения электрона принимают вид:

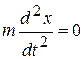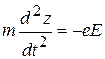, . (4)

Интегрируя эти уравнения, получим:

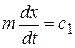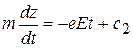, . (5)

Постоянные 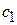и 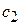можно определить, положив t = 0. Тогда составляющие скорости электрона по осям будут равны составляющим его начальной скорости :

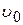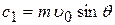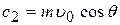, . (6)

Таким образом, составляющие скорости в процессе движения

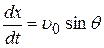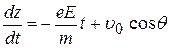, . (7)

Интегрируя повторно, получим:

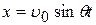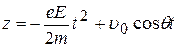, . (8)

Постоянные интегрирования при этом, очевидно, равны нулю, так как в момент t = 0 электрон находился в начале координат (х = 0, z = 0).

Согласно (8)

.

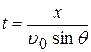Подставляя это выражение в (8), получим:

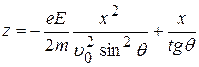, (9а)

или

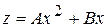(9б)

где

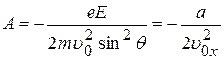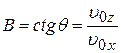, . (10)

В выражении (10) величина ( 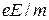) обозначена через а. Она определяет ускорение электрона в соответствии с аналогией уравнения (8) уравнению равнозамедленного движения тела.

Представляет интерес, встречающийся в ряде электронных приборов случай,когда вектор начальной скорости электрона 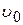нормален к вектору напряженности поля Е: 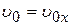. По-прежнему в момент t = 0 электрон находится в начале координат (х = 0, у = 0, z = 0) и

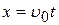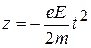, . (11)

Определяя из первого уравнения время 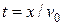и подставляя его во второе уравнение, получим:

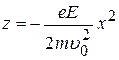. (12)

Электрон будет двигаться в плоскости xOz по параболе, отклоняясь от оси х под воздействием ускоряющего поля Е (рис. 2). Этот случай движения электрона характерен для электроннолучевых приборов, в которых поперечное поле используется для отклонения электронного потока.

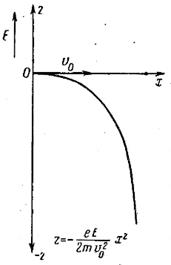
Рис. 2. Движение электрона в однородном электрическом поле в случае .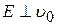

Для определения траектории движения электрона в электрическом поле можно применить законы электронной оптики, используя отмеченную выше аналогию между электрическими полями и оптическими средами. Пусть, например, вектор начальной скорости 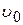электрона направлен под углом q₁ к вектору напряженности электрического поля Е (рис. 3).

Выделим элементарный участок поля, на котором потенциал изменяется от U₁ до U₂. Ввиду однородности поля эквипотенциальные поверхности (поверхности, все точки которых обладают одним и тем же потенциалом) U₁ и U₂ являются плоскостями. При движении электрона из точки 1 в точку 2 под воздействием ускоряющего электрического поля увеличивается составляющая его скорости, нормальная к эквипотенциальным плоскостям: 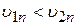. Тангенциальная же составляющая его скорости остается неизменной: 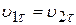. Вследствие этого угол между вектором скорости электрона и нормалью к эквипотенциальным плоскостям изменяется: .

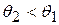Из условия равенства тангенциальных составляющих скорости 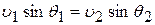можно получить:

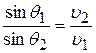, (13)

или

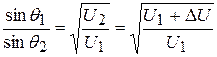. (14)

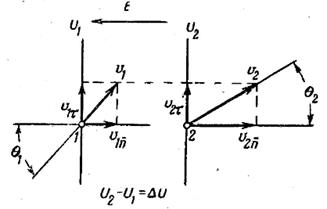
Рис. 3. Изменение составляющих скорости электрона при его движении в электрическом поле.

Выражение (13) аналогично формуле преломления светового луча на границе оптических сред:

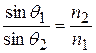, (15)

где 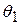и 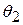— угол падения и угол преломления светового луча соответственно, а 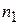и 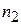— коэффициенты оптической плотности двух сред.

Пользуясь выражением (14), легко найти „угол преломления" для плоского конденсатора, который является „преломляющей призмой" (рис. 4). В этом случае 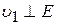и

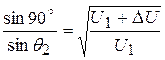, (16)

или

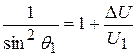. (17)

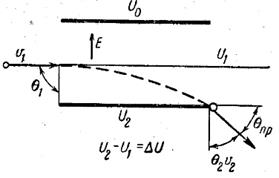
Рис. 4. Движение электрона в поле плоского конденсатора.

Отсюда легко определить угол преломления:

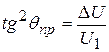. (18)