Движение электронов в неоднородном магнитном поле

Задача аналитического описания неоднородных магнитных полей встречает не меньшие трудности, чем в случае неоднородного электрического поля. Поэтому для определения картины неоднородного магнитного поля применяются, как правило, экспериментальные методы. Один из наиболее простых и распространенных — баллистический метод. Небольшую катушку, к которой подключен баллистический гальванометр, помещают в выбранную точку магнитного поля, так чтобы ось катушки совпадала с направлением магнитных силовых линий. Затем катушку быстро удаляют из поля и по величине наведенной в катушке э.д.с. находят напряженность поля в данной точке. Построенные по точкам силовые линии неоднородного поля используются для определения траектории электрона при его движении в этом поле.

Неоднородные магнитные поля создаются для фокусирования параксиальных пучков электронов. Обычно используются короткие катушки – многослойные соленоиды, длина которых соизмерима с внутренним диаметром.

Рассмотрим движение электрона в неоднородном магнитном поле такой катушки (рис. 12).

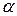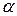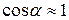Вектор скорости электрона направлен под углом к оси катушки. Разложим вектор Н напряженности магнитного поля в точке А на радиальную Н_r и аксиальную Н_а составляющие. Угол мал, , и можно считать, что 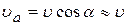. На электрон действует сила 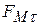(рис. 12,б), перпендикулярная плоскости чертежа и вызывающая вращательное движение электрона вокруг оси катушки. Под действием этой силы появляется тангенциальная составляющая скорости электрона 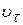(рис. 12,в), которая совместно с Н_а образует силу 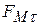, прижимающую электрон к оси. Таким образом, в неоднородном магнитном поле электрон движется по спирали с уменьшающимся радиусом и в некоторой точке С его траектория соприкасается с осью катушки.

Фокусное расстояние такой магнитной линзы, если пучок падающих электронов считать параллельным, определяется выражением:

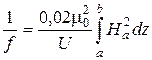, (36)

где 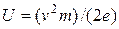- потенциал, определяющий скорость движения электрона вдоль оси катушки, а интегрирование осуществляется вдоль оси в пределах a-b неоднородного магнитного поля.

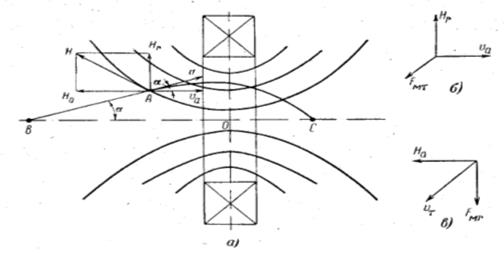
Рис. 12. Магнитная линза, образованная полем короткой катушки. а — магнитное поле; б и в — векторные диаграммы.

Если U выражено в вольтах, а Н — в эрстедах, то фокусное расстояние поучается в сантиметрах. Такая линза всегда является собирающей, так как ее оптическая сила не зависит от направления силовых линий поля.

5. Движение электронов в скрещенных электрическом и магнитном полях

Скрещенные электрическое и магнитное поля используются для управления электронным потоком во многих электронных приборах. В этом случае сила, действующая на' электрон, равна сумме сил действия электрического и магнитного полей в отдельности:

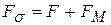, (37)

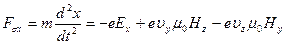, (38а)

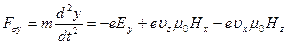, (38б)

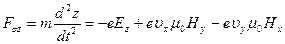. (38в)

Рассмотрим частный случай движения электрона в суммарном поле, когда векторы Е и H взаимно перпендикулярны. Электрическое поле образовано двумя плоскими параллельными электродами к и а (рис. 13), разность потенциалов которых 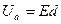, где d - расстояние между электродами;

; ;

; ;

; .

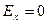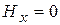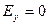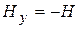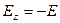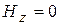Электрон находится в начале координат (x=y=z=0), его начальная скорость 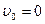и уравнения (38) принимают вид:

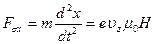, (39а)

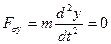, (39б)

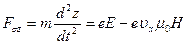. (39в)

Движение электрона будет происходить в плоскости хОу.

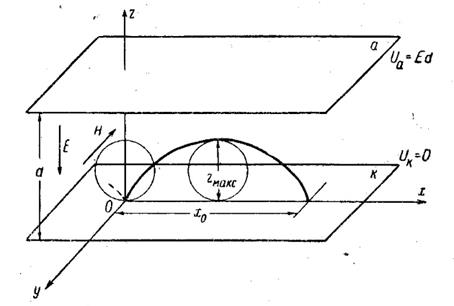
Рис. 13. Движение электрона во взаимно перпендикулярных

однородных электрическом и магнитном полях .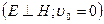

Рассмотренные нами случаи окажутся весьма полезными при изучении движения электронов в сверхвысокочастотных генераторах — магнетронах. Следует, однако, отметить, что магнетрон имеет цилиндрическую, а не плоскую конструкцию электродов и, кроме того, движение электрона в нем сопровождается увеличением или уменьшением энергии. Это обстоятельство мы рассмотрим при изучении магнетронов. Здесь же, анализируя движение электрона в скрещенных радиальном электрическом и аксиальном магнитном полях, будем считать, что 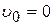и электрон перемещается по эпициклоиде (см. рис. 14).

На рис. 15 изображены траектории электрона для Н=const и различных значений напряженности поля Е между анодом и катодом. При r_а – r_к = const и U_K = 0 они соответствуют различным величинам U_а.

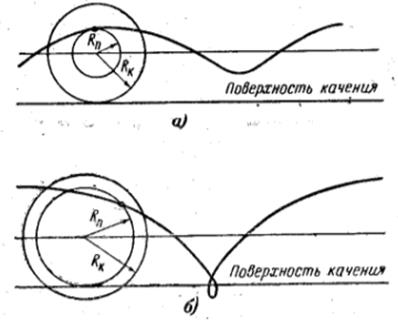
Рис. 14. Траектории движения электрона по укороченной (а) и удлиненной (б) циклоидам.

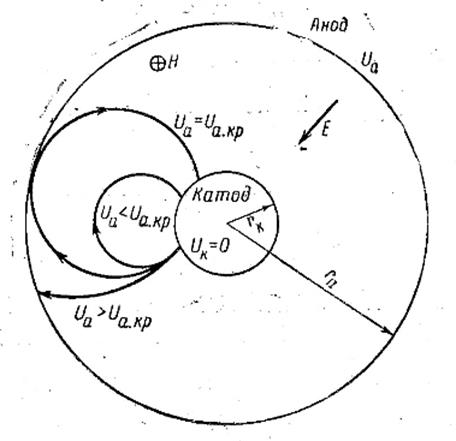
Рис. 15. Траектории электрона в цилиндрическом диоде, помещенном в магнитное поле, при различных значениях U_а.

Когда U_а мало, электрон, двигаясь по витку эпициклоиды, возвращается на катод. Увеличение потенциала анода сопровождается возрастанием радиуса R_K, и при некотором значении U_а= U_а.кр. максимальное удаление электрона от катода приближенно равно разности радиусов анода и катода r_а – r_к.

Рис. 16. Парабола критического режима.

Потенциал, при котором электрон лишь касается поверхности анода, называется критическим анодным потенциалом U_а.кр.. При U_а 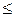U_а.кр. электроны не достигают анода, а если U_а>U_а.кр., то все электроны попадают на анод. Значение U_а.кр. для плоских электродов можно определить из отношения (40). Для них

,

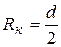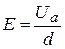
и, следовательно,

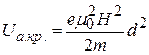. (40)

Для цилиндрических электродов

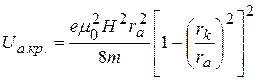. (41)

Зависимость 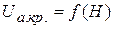, представленная на рис. 16, называется параболой критического режима.