Движение электронов в неоднородном электрическом поле

В электронных приборах электростатические поля обычно создаются совокупностью различных по форме электродов, которые находятся под тем или иным потенциалом. Как правило, такие поля являются неоднородными, и если в пространстве нет других зарядов, то такое электростатическое поле описывается уравнением Лапласа:

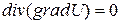. (19)

Решение этого уравнения в общем виде практически невозможно, а для более простых случаев, например аксиально-симметричных полей, встречает серьезные затруднения.

На практике конфигурация неоднородных электростатических полей определяется экспериментально. Одним из наиболее распространенных является метод электролитической ванны, заключающийся в следующем. В плоскую ванну (рис. 5), выполненную из диэлектрического материала, помещают модели электродов. Конфигурация их и взаимное расположение в точности соответствуют конфигурации и расположению электродов в приборе, поле в котором подлежит исследованию. При этом все линейные размеры могут быть увеличены в n раз, что при полном геометрическом подобии поля приведет лишь к уменьшению напряженности в любой точке поля в 1/ n раз. Моделям электродов сообщаются потенциалы, равные или в m раз большие истинных потенциалов в приборе. Пропорциональное увеличение потенциалов на всех электродах также не нарушает конфигурации поля и приводит лишь к увеличению напряженности поля в m раз.

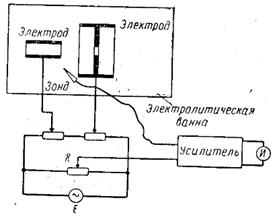
Рис. 5. Устройство электролитической ванны.

Ванна с электродами наполняется каким-либо электролитом, обычно водой. Для исключения влияния электролиза на проводимость электролита к электродам обычно подводят переменное напряжение (генератор E). К токопроводящему зонду от того же генератора с делителя R подается регулируемое переменное напряжение. В цепь зонда включается усилитель с нуль-индикатором на выходе. Если зонд опустить в какую-либо точку ванны, то в цепи зонда потечет ток, обусловленный разностью потенциалов между данной точкой поля и зондом. Регулируя потенциометром R напряжение, подводимое к зонду, можно добиться равенства потенциалов и, следовательно, отсутствия тока в цепи зонда. Фиксируя точки поля с одинаковым потенциалом, получают сечение одной из эквипотенциальных поверхностей. Измерения повторяют при различных напряжениях зонда и строят семейство эквипотенциальных кривых.

Зная картину неоднородного электрического поля, можно воспользоваться методами графического построения траекторий электронов. Один из этих методов, основанный на законе преломления, заключается в построении траектории электрона в виде ломаной линии, отрезки которой ограничены соседними эквипотенциальными поверхностями. Изменение направления движения электрона для случая, показанного на рис. 3, можно определить, воспользовавшись соотношением (14). Однако обычно разность потенциалов для соседних эквипотенциальных поверхностей невелика и оперирование с синусами малых углов, а также геометрическое построение этих углов затруднительны.

Один из практических методов построения траектории электрона иллюстрируется рис. 6.

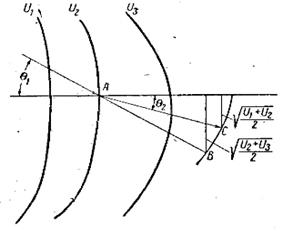
Рис. 6. Построение траектории движения электрона в неоднородном электрическом поле.

Направление движения электрона, падающего на поверхность U₁ под углом q₁, продолжают до точки В, отстоящей от нормали к поверхности U₁ на величину 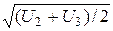. Затем из точки А через точку В проводят дугу окружности и отмечают на ней точку С, отстоящую от нормали на величину 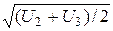. Соединив точки А и С, определяют направление движения электрона между поверхностями U₂ и U₃. Продолжив построение для следующих пар эквипотенциальных поверхностей, получают траекторию электрона в неоднородном поле в виде ломаной линии, которую без существенной погрешности можно заменить плавной кривой. Неоднородные электрические поля, широко используемые в электронных приборах для изменения скорости и направления движения электронов, называются электронными линзами. В электронной оптике различают линзы-диафрагмы, одиночные линзы, иммерсионные линзы и иммерсионные объективы.

Примеры линз-диафрагм показаны на рис. 7; там же приведены кривые распределения потенциалов вдоль оси линзы. Линзы-диафрагмы, образованные электродами с круглыми отверстиями, могут быть собирающими и рассеивающими. В собирающей линзе в плоскости диафрагмы 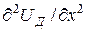> 0; в рассеивающей линзе, наоборот, 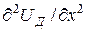< 0. Фокусное расстояние линз-диафрагм можно определить по формуле

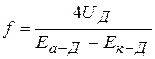, (20)

где 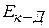— напряженность поля слева, а 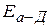— справа от диаграммы.

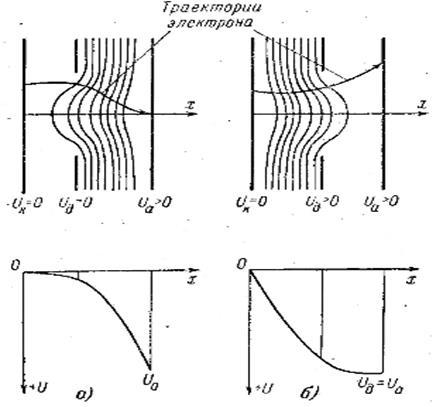
Рис. 7. Электронные линзы — диафрагмы и распределение потенциала в них: а — собирающая; б — рассеивающая.

Одиночные линзы образуются системой линз-диафрагм и характеризуются постоянными и равными потенциалами по обе стороны линз. Пример одиночной линзы показан на рис. 8.

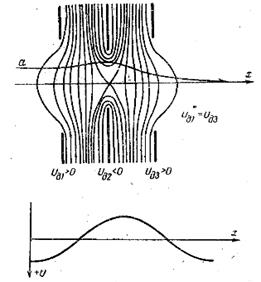
Рис. 8. Одиночная электронная линза и распределение потенциала в ней

3. Движение электронов в однородном магнитном поле

Перемещение электрических зарядов в магнитном поле при условии, что траектория движения заряда пересекает силовые линии поля, определяется силой, действующей на этот заряд:

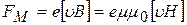. (21)

В международной системе единиц 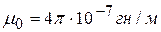. Для вакуума .

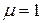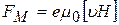. (22)

Вектор силы 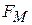нормален к плоскости, в которой расположены векторы — сомножители 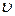и Н. Направление вектора 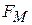— силы Лоренца легко найти, пользуясь правилом правой руки.

Рассмотрим, какая работа затрачивается при перемещении электрона в магнитном поле:

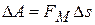. (23)

Подставляя сюда (22) и учитывая, что 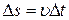, получим:

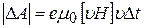, (24)

так как скалярное произведение двух взаимно перпендикулярных векторов F_M и 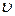равно нулю.

Это означает, что кинетическая энергия электрона при его движении в магнитном поле остается неизменной. Другими словами, магнитное поле не может замедлить или ускорить движение электронов. Из выражения (22): На электрон, находящийся в покое, движущийся параллельно силовым линиям, магнитное поле не оказывает никакого воздействия ( 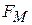= 0). Оно может изменить направление движения электрона и только в том случае, если начальная скорость электрона не равна нулю, и при своем движении он пересекает силовые линии магнитного поля.

Используя проекции векторов 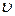и Н на оси координат, можно выражение (22) записать в виде:

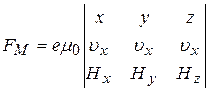. (25)

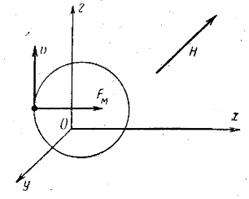
Рис. 9. Движение электрона в однородном магнитном поле

в случае .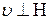

Раскрывая детерминант и учитывая, что F = ma, получим выражение для составляющих силы F_M по осям координат:

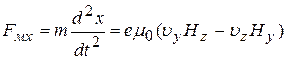, (26a)

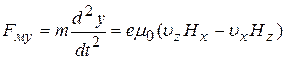, (26б)

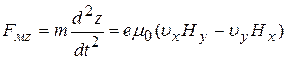. (26в)

Рассмотрим случай, когда вектор скорости электрона 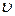нормален к силовым линиям магнитного поля Н. Как видно из рис. 9:

, ,

, ,

, .

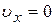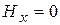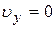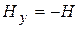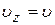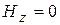При этом условии система уравнений (26) примет вид:

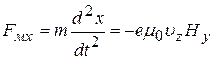, (27а)

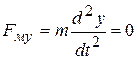, (27б)

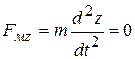. (27в)

На электрон действует сила, направленная вдоль оси х:

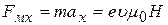. (28)

Эта сила сообщает электрону ускорение, вектор которого совпадает с направлением силы 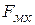и, следовательно, перпендикулярен 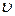. Отсюда видно, что ускорение 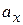является центростремительным и движение электрона происходит по криволинейной траектории.

Таким образом,

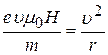(29)

и отсюда

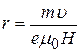. (30)

Здесь m = const; e = const, Н = const, так как поле однородно, и 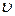=const. Таким образом, радиус кривизны траектории также остается неизменным: r = const. Этому условию удовлетворяет только окружность.

Рассмотрим более общий случай, когда вектор скорости электрона не лежит ни в одной из координатных плоскостей, а вектор напряженности поля Н направлен вдоль одной из осей, например, вдоль оси х (рис. 10). Спроектируем вектор начальной скорости электрона на координатные оси. В этом случае уравнения (26) запишутся в виде

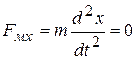, (31а)

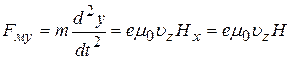, (31б)

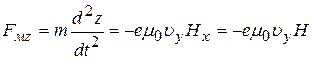. (31в)

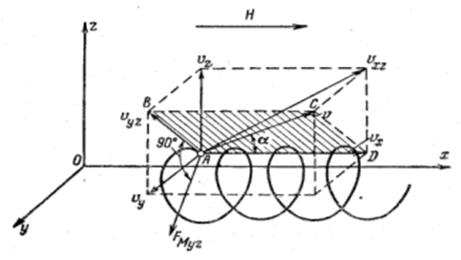
Рис. 10. Общий случай движения электрона в однородном магнитном поле.

Обе действующие на электрон силы лежат в плоскости уОz. Суммарная сила, действующая на электрон, перпендикулярна плоскости ABCD, содержащей векторы Н и 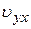, и определяется из соотношения

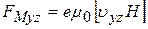. (32)

Под действием этой силы электрон вращается по окружности, лежащей в плоскости yOz. Кроме того, под действием составляющей начальной скорости, направленной вдоль оси х, электрон движется поступательно вдоль этой оси. Результирующей траекторией электрона является спираль, ось которой параллельна оси х, а радиус витка в соответствии с (30) равен:

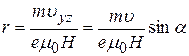. (33)

Один оборот спирали электрон совершит за время 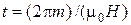, переместясь со скоростью 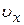вдоль оси х на шаг спирали:

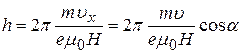. (34)

Однородное магнитное поле в некоторых электроннолучевых приборах используется в качестве магнитной электронной линзы, фокусирующей поток электронов, выходящий с поверхности катода под некоторым углом 2 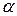(рис. 11).

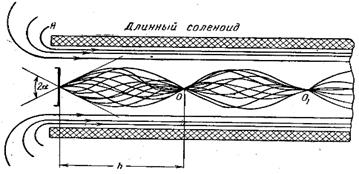
Рис. 11. Магнитная линза, образованная полем длинной катушки.

Если угол 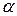невелик, то такой пучок электронов называют параксиальным. Фокусирующее действие однородного магнитного поля, создаваемого обычно длинным соленоидом, основано на равенстве шага спиральных траекторий всех электронов. Уго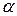л мал, 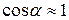, и шаг спирали

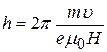(35)

не зависит от направления вектора начальной скорости электронов. В точках О, О₁ и др., отстоящих друг от друга на величину h, траектории электронов касаются оси соленоида. Происходит фокусирование электронного пучка.