Вероятностный подход к описанию погрешностей. Законы распределения и их числовые характеристики.

Полным описанием случайной величины, а следовательно и погрешности, является ее закон распределения, которым определяется характер появления различных результатов отдельных измерений.

В практике электрических измерений встречаются различные законы распределения, некоторые из которых рассмотрены ниже.

Нормальный закон распределения (закон Гаусса). Этот закон является одним из наиболее распространенных законов распределения погрешностей. Объясняется это тем, что во многих случаях погрешность измерения образуется под действием большой совокупности различных, независимых друг от друга причин. На основании центральной предельной теоремы теории вероятностей результатом действия этих причин будет погрешность, распределенная по нормальному закону при условии, что ни одна из этих причин не является существенно преобладающей.

Нормальный закон распределения погрешностей описывается формулой

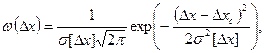
где ω(Δx) —плотность вероятности погрешности Δx; σ[Δx]— среднее квадратическое отклонение погрешности; Δx_c — систематическая составляющая погрешности.

Вид нормального закона представлен на рис. 1,а для двух значений σ[Δx]. Так как

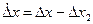, то закон распределения случайной составляющей погрешности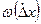

имеет тот же вид (рис 1,б) и описывается выражением

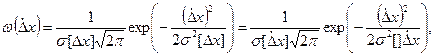
где 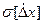— среднее квадратическое отклонение случайной составляющей погрешности; 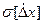= σ[Δx]

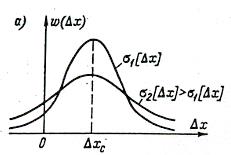
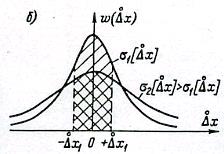
Рис. 1. Нормальный закон распредёления погрешности измерений (а) и случайной составляющей погрешности измерений (б)

Таким образом, закон распределения погрешности Δx отличается от закона распределения случайной составляющей погрешности 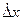только сдвигом по оси абсцисс на величину систематической составляющей погрешности Δх_с.

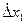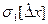Из теории вероятностей известно, что площадь под кривой плотности вероятности характеризует вероятность появления погрешности. Из рис.1, б видно, что вероятность Р появления погрешности в диапазоне ± при больше, чем при 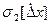(площади, характеризующие эти вероятности, заштрихованы). Полная площадь под кривой распределения всегда равна 1, т. е. полной вероятности.

Учитывая это, можно утверждать, что погрешности, абсолютные значения которых превышают 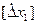появляются с вероятностью, равной 1 — Р, которая при 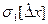меньше, чем при 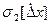. Следовательно, чем меньше 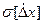, тем реже встречаются большие погрешности, тем точнее выполнены измерения. Таким образом, Среднее квадратическое отклонение 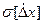можно использовать для характеристики точности измерений:

Равномерный закон распределения. Если погрешность измерений с одинаковой вероятностью может принимать любые значения, не выходящие за некоторые границы, то такая погрешность описывается равномерным законом распределения. При этом плотность вероятности погрешности ω(Δx) постоянна внутри этих границ и равна нулю вне этих границ. Равномерный закон распределения представлен на рис. 2. Аналитически он может быть записан так:

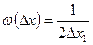при –Δx₁ ≤ Δx ≤ + Δx₁;

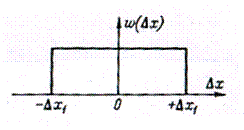
Рис 2. Равномерный закон распределения

С таким законом распределения хорошо согласуется погрешность от трения в опорах электромеханических приборов, не-исключенные остатки систематических погрешностей, погрешность дискретности в цифровых приборах.

Трапециевидный закон распределения. Это распределение графически изображено на рис.3, а. Погрешность имеет такой закон распределения, если она образуется из двух независимых составляющих, каждая из которых имеет равномерный закон распределения, но ширина интервала равномерных законов различна. Например, при последовательном соединении двух измерительных преобразователей, один из которых имеет погрешность, равномерно распределенную в интервале ±Δx₁, а другой — равномерно распределенную в интервале ± Δx₂, суммарная погрешность преобразования будет описываться трапециевидным законом распределения.

Треугольный закон распределения (закон Симпсона). Это распределение (см. рис.3, б) является частным случаем трапециевидного, когда составляющие имеют одинаковые равномерные законы распределения.

Двухмодальные законы распределения. В практике измерений встречаются двухмодальные законы распределения, т. е. законы распределения, имеющие два максимума плотности вероятности. В двухмодальный закон распределения, который может быть в приборах, имеющих погрешность от люфта кинематических механизмов или от гистерезиса при перемагничивании деталей прибора.

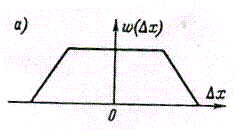
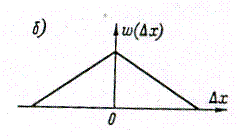
Рис.3. Трапециевидный (а) и треугольный (б) законы распределения