Центр и моменты распределения.

В результате измерения получают значение измеряемой величины в виде числа в принятых единицах величины. Погрешность измерения тоже удобно выражать в виде числа. Однако погрешность измерения является случайной величиной, исчерпывающим описанием которой может быть только закон распределения. Из теории вероятностей известно, что закон распределения можно охарактеризовать числовыми характеристиками (неслучайными числами), которые и используются для количественной оценки погрешности.

Основными числовыми характеристиками законов распределения являются математическое ожидание и дисперсия, которые определяются выражениями:

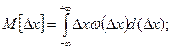
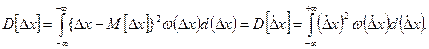
где М — символ математического ожидания; D — символ дисперсии.

Математическое ожидание погрешности измерений есть неслучайная величина, относительно которой рассеиваются другие значения погрешностей при повторных измерениях. Математическое ожидание характеризует систематическую составляющую погрешности измерения, т. е. М [Δх]=Δx_C. Как числовая характеристика погрешности

М [Δх] показывает на смещенность результатов измерения относительно истинного значения измеряемой величины.

Дисперсия погрешности D [Δх] характеризует степень рассеивания (разброса) отдельных значений погрешности относительно математического ожидания. Так как рассеивание происходит за счет случайной составляющей погрешности то .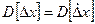

Чем меньше дисперсия, тем меньше разброс, тем точнее выполнены измерения. Следовательно, дисперсия может служить характеристикой точности проведенных измерений. Однако дисперсия выражается в единицах погрешности в квадрате. Поэтому в качестве числовой характеристики точности измерений используют среднее квадратическое отклонение 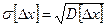с положительным знаком и выражаемое в единицах погрешности.

Обычно при проведении измерений стремятся получить результат измерения с погрешностью, не превышающей допускаемое значение. Знание только среднего квадратического отклонения не позволяет найти максимальную погрешность, которая может встретиться при измерениях, что свидетельствует об ограниченных возможностях такой числовой характеристики погрешности, как σ[Δx]. Более того, при разных условиях измерений, когда законы распределения погрешностей могут отличаться друг от друга, погрешность с меньшей дисперсией может принимать большие значения.

Максимальные значения погрешности зависят не только от σ[Δx], но и от вида закона распределения. Когда распределение погрешности теоретически неограниченно, например при нормальном законе распределения, погрешность может быть любой по значению. В этом случае можно лишь говорить об интервале, за границы которого погрешность не выйдет с некоторой вероятностью. Этот интервал называют доверительным интервалом, характеризующую его вероятность — доверительной вероятностью, а границы этого интервала — доверительными значениями погрешности.

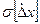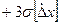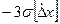В практике измерений применяют различные значения доверительной вероятности, например: 0,90; 0,95; 0,98; 0,99; 0,9973 и 0,999. Доверительный интервал и доверительную вероятность выбирают в зависимости от конкретных условий измерений. Так, например, при нормальном законе распределения случайных погрешностей со средним квадратическим отклонением часто пользуются доверительным интервалом от до ,для которого доверительная вероятность равна

0,9973. Такая доверительная вероятность означает, что в среднем из 370 случайных погрешностей только одна погрешность по абсолютному значению будет

больше 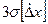.Так как на практике число отдельных измерений редко превышает несколько десятков, появление даже одной случайной погрешности, большей, чем

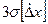,маловероятное событие, наличие же двух подобных погрешностей почти невозможно. Это позволяет с достаточным основанием утверждать, что все возможные случайные погрешности измерения, распределенные по нормальному закону, практически не превышают по абсолютному значению 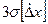(правило «трех сигм»).

В соответствии с ГОСТ доверительный интервал является одной из основных характеристик точности измерений. Одну из форм представления результата измерения этот стандарт устанавливает в следующем виде: x; Δx от Δx_н до Δx_в¹; Р, где x — результат измерения в единицах измеряемой величины; Δx, Δx_н , Δx_в — соответственно погрешность измерения с нижней и верхней ее границами в тех же единицах; Р — вероятность, с которой погрешность измерения находится в этих границах.

ГОСТ допускает и другие формы представления результата измерения, отличающиеся от приведенной формы тем, что в них указывают раздельно характеристики систематической и случайной составляющих погрешности измерения. При этом для систематической погрешности указывают ее вероятностные характеристики. Ранее уже отмечалось, что иногда систематическую погрешность приходится оценивать с вероятностных позиций. В этом случае основными характеристиками систематической погрешности являются М [Δх_с],σ [Δх_с]и ее доверительный интервал. Выделение систематической и случайной составляющих погрешности целесообразно, если результат измерения будет использован при дальнейшей обработке данных, например при определении результата косвенных измерений и оценке его точности, при суммировании погрешностей и т. п.

Любая из форм представления результата измерения, предусмотренная ГОСТ должна содержать необходимые данные, на основании которых может быть определен доверительный интервал для погрешности результата измерения. В общем случае доверительный интервал может быть установлен, если .известен вид закона распределения погрешности и основные числовые характеристики этого закона.

________________________

¹ Δx_н и Δx_в должны быть указаны со своими знаками. В общем случае |Δx_н| может быть не равна |Δx_в|. Если границы погрешности симметричны, т.е. |Δx_н| = |Δx_в| = Δx, то результат измерения может быть записан так: x ±Δx; P.

Вероятностный подход к описанию погрешностей. Грубые погрешности,