Использование безрисковых займов и кредитов

Рассмотренная выше модель Марковица позволяет сформировать оптимальный портфель состоящий только из рисковых активов. Инвестор, однако, может создать портфель, включающий наряду с рисковыми и безрисковый актив. Этот актив имеет нулевой риск и некоторую безрисковую доходность, которую обозначим через R_f (см. рис 5.4.). Точка R_f соответствует ситуации, когда портфель сформирован только из безрисковых активов. Комбинация безрискового и рискового актива упрощает зависимость между риском и доходностью портфеля. Точка А соответствует ситуации, когда портфель составлен только из рисковых активов. Возможные портфели сформированные из комбинации рисковых и безрисковых активов будет располагаться на прямой, соединяющей точку безрисковой доходности и точку А пересечения этой линией эффективного множества рисковых портфелей. Вид линии R_fА обусловлен отсутствием корреляционной зависимости между безрисковым активом с одной стороны и рисковым активом с другой, т.е. при комбинации рисковых и безрисковых активов эффект диверсификации не возникает.

Рассмотренное взаимоотношение между риском и доходностью известна как модель оценки капитальных активов (capital asset pricing model CAPM). В соответствии с моделью CAPM инвесторы формируют портфель не только из рисковых активов, а определяют доли средств направляемых в рисковые и безрисковые активы. Точки на прямой R_fА находящиеся вблизи точки А соответствуют портфелям, сформированным в основном их рисковых активов, а вблизи точки R_f – из безрисковых.

Рис. 5.4. Достижимое множество портфелей в модели CAPM

Выбор соотношения между риском и доходностью при использовании безрисковых активов существенно отличается от модели Марковица. В рамках последней модели инвесторы ищут конкретный портфель рисковых активов, соответствующий их отношению к риску. В данном случае инвестор определяет риск портфеля путем выбора соотношения между рисковыми и безрисковыми активами. Так, например, инвесторы менее склонные к риску большую часть своих средств помещают в государственные ценные бумаги, а более терпимые к риску – в корпоративные ценные бумаги.

На представленном выше рисунке можно провести сотни линий, соединяющих точку R_f и линию эффективных портфелей. Из них необходимо выбрать такую, которая является наилучшей для инвестора, т.е. обеспечивает наилучшее соотношение между доходностью и риском.

Так например портфели, лежащие на линии R_fА не являются эффективными, так как любому портфелю, лежащему на этой линии может быть противопоставлен портфель с большей доходностью при том же самом уровне риска. Например, портфель Р2 имеет более высокую доходность при том же уровне риска (см. рис. 5.5).

Рис. 5.5. Эффективное множество портфелей при использовании безрискового актива

Следовательно, эффективные портфели будут лежать на линии, которая имеет наибольший наклон по отношению к горизонтальной оси. Эта линия выходит из точки R_f и является касательной по отношению к кривой, соответствующей эффективному множеству в модели Марковица. Портфели, лежащие на прямой R_fМ обеспечивают наибольшую доходность при заданном уровне риска.

Эта единственную линию называют линией рынка капитала (Capital Market Line). Точка М соответствует рыночному портфелю, т.е. портфелю составленному из всех рисковых активов. Каждый актив в рыночном портфеле представлен в пропорции соответствующий его доли на рынке. Так, например, на фондовом рынке США доля компании General Motors составляет один процент рисковых активов. Исходя из этого доля акций данной компании в рыночном портфеле также должна составлять один процент. В реальных ситуациях сформировать идеальный рыночный портфель представляется невозможным и в качестве его заменителя рассматриваются портфели, используемые для расчета рыночных индексов, например S&P 500 Index. Индекс рассчитывается на основе курса акций пятисот ведущих компаний. При этом, чем более крупной является компания, тем больше ее вклад в значение индекса.

Уравнение линии рынка капитала имеет следующий вид

R_p = R_f + [(R_m - R_f)/ ]* ,

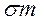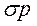где R_p –ожидаемая доходность портфеля, состоящего из рисковых и безрисковых активов, величина (R_m - R_f)/ 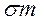характеризует тангенс угла наклона линии рынка капитала.