Оптимизация портфеля, состоящего из двух ценных бумаг

Как было показано ранее доходность и среднеквадратичное отклонение портфеля, состоящего из двух активов определяется следующими соотношениями:

Rp = R1*W1+R2*W2

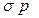= ( ²*W_х² + ²*W_у² +2*W_х* W_у* * *CR_xy)^1/2

Рассмотрим задачу определение структуры портфеля, обеспечивающего минимальный уровень риска. Обозначим за W – доля актива Х в портфеле, тогда (1- W) будет доля актива У. С учетом этого выражение для стандартного отклонения портфеля будет иметь вид:

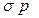= ( ²* W ² + ²*(1- W)² +2* W * (1- W)* * *CR_xy)^1/2

При заданных значениях и CR_xy величина стандартного отклонения портфеля 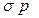является функцией W. Необходимым условием экстремума функции является равенство нулю ее первой производной. Продифференцируем данную функция по переменной W и приравняем первую производную к нулю:

(2* ²* W – 2* ²*(1- W) +2* (1-2 W)* * *CR_xy)^1/2) ₌₀

2*( ²* W ² + ²*(1- W)² +2* W * (1- W)* * *CR_xy)^1/2

Из данного выражения получаем

W = ( ² - * *CR_xy)/( ²+ ²- 2 * *CR_xy)

Полученное выражение позволяет определить удельный вес активов в портфеле, обеспечивающий минимальный риск.

Рассмотрим ряд частных случаев.

1. Между активами имеет место наибольшая отрицательная ковариация, т.е. CR_xy = -1.

Выражение для удельного веса актива Х в этом случае будет иметь вид

W = ( ² + * )/( ²+ ²+ 2 * ) = /( + )

1- W = /( + )

Для нахождения среднеквадратичного отклонения портфеля необходимо подставить полученные выражения для удельных весов активов в исходное выражение для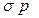

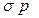= ( ²*W_х² + ²*W_у² +2*W_х* W_у* * *CR_xy)^1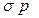/2

= ( ²*[ /( + )]² + ²*[ /( + )]²-2*[ /( + )]* [ /( + )]* * )^1/2 = 0.

Таким образом, при абсолютной отрицательной ковариации между активами можно определить такие их удельные веса, что риск портфеля будет равен нулю.

2. Рассмотрим далее случай ковариации активов равной нулю, т.е. CR_xy = 0. Подставляя в выражение

W = ( ² - * *CR_xy)/( ²+ ²- 2 * *CR_xy)

CR_xy = 0, Получим:

W = ( ² )/( ²+ ²)

1- W = ( ² )/( ²+ ²)

Риск портфеля в этом случае будет равен

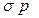= */( ²+ ²)^1/2

2. Третий случай будет соответствовать абсолютной положительной ковариации активов Х и У. Подставим в выражение

W = ( ² - * *CR_xy)/( ²+ ²- 2 * *CR_xy)

CR_xy = 1, Получим

W = /( - )

1- W = - /( - )

Минимальный риск портфеля в этом случае достигается при отрицательном удельном весе одного из активов в портфеле.

Пример. Рассмотрим две ценные бумаги Х и У. Их среднемесячная доходность представлена в таблице 5.6.

Таблица 5.6