Определение деформаций и напряжений. 4 страница

1. Построение функций форм (интерполирующих функций), удовлетворяющих всем необходимым условиям, для элементов с криволинейными границами является очень сложной задачей.

2. Интегралы, возникающие в выражении элементных матриц жесткости и узловых векторов, уже не могут быть вычислены в замкнутой форме.

Имеющиеся трудности оказываются преодолимыми, если использовать концепцию изопараметрического элемента совместно с квадратурами численного интегрирования. Комбинация этих идей произвела революцию в методе конечных элементов в конце шестидесятых годов прошлого века.

В настоящей и следующей лекциях концепция изопараметрического представления будет рассмотрена на примере двумерных треугольных и четырехсторонних элементов.

Исходные понятия

Рассмотренный в предыдущих лекциях линейный треугольный конечный элемент представляет собой простейший изопараметрический элемент, хотя его уравнения и были получены другим путем. Запишем основные соотношения этого элемента:

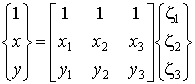,	(9.1а)
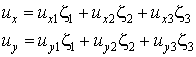,	(9.1б)
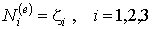,	(9.1в)

Интерпретация приведенных уравнений следующая. Треугольные координаты определяют геометрию с помощью соотношения (9.1а). Интерполирующее соотношение для перемещений (9.1б) задано с помощью функций формы элемента 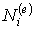, которые в случае линейного треугольного элемента совпадают с треугольными координатами. Таким образом, и геометрия элемента (глобальные координаты), и основные переменные (перемещения) оказываются заданны с помощью одинаковых интерполирующих соотношений. Такие элементы носят название изопараметрических.

Очевидно, что можно представить плоский треугольный элемент, у которого функция, аппроксимирующая перемещения, задана полиномом более высокого порядка относительно треугольных координат 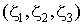по сравнению с линейной геометрией элемента. Такие элементы носят название суперпараметрических. Для полноты отметим, что если имеет место обратная ситуация, то элементы носят название субпараметрических. В некоторых случаях применения неизопараметрических элементов оказывается оправданным.

Вернемся к рассмотрению изопараметрического элемента. Перепишем соотношения (9.1а-в) в универсальном виде, чтобы подчеркнуть их внутреннее единство:

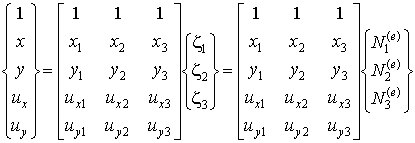
(9.2)

Формула (9.2) подчеркивает тот факт, что геометрия и перемещения заданы одним и тем же параметрическим представлением с помощью функций формы 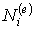. В этом и состоит ключевая идея изопараметрического подхода в методе конечных элементов.

Рассмотренная методика легко распространяется на случай произвольного по геометрии элемента, включая и трехмерные элементы, что показано на Рис. 9.1. При этом термин «треугольные координаты» заменяется на более общее понятие «естественные локальные координаты», которые также могут быть интерпретированы как параметры, определяющие соответствующие функции формы элемента.

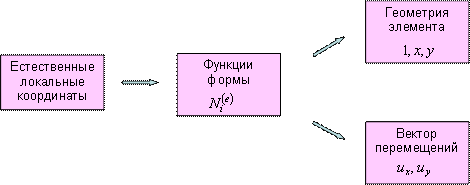
Рис. 9.1. Изопараметрический подход в методе конечных элементов.

Общая изопараметрическая формулировка упругого двумерного элемента

Рассмотрим общую изопараметрическую формулировку упругого двумерного элемента, содержащего n узлов. Для описания элемента требуются два типа интерполирующих соотношений: одно для задания геометрии элемента и другое для аппроксимации вектора перемещений на элементе. Оба соотношения строятся с помощью одинаковых функций формы и соответствующих значений функций (глобальных координат и компонент перемещений) в узлах элемента. Таким образом, получаем:

Геометрические соотношения (интерполяция координат):

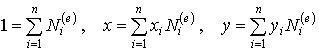
(9.3)

Функциональные соотношения (интерполяция перемещений):

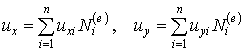
(9.4)

Уравнения (9.3) и (9.4) могут быть представлены в виде единой формулы в матричном виде:

(9.5)

Первые три уравнения в (9.5) определяют геометрию элемента, последние два задают аппроксимацию перемещений на элементе. Заметим, что изопараметрический подход позволяет добавлять в систему (9.5) другие функции, зависящие от координат точек элемента, если их интерполяционное соотношение задано с помощью тех же самых функций формы. Например, предположим, что толщина пластины h изменяется, а также, что температурное поле Т - переменное на элементе (в случае термоупругой задачи). Тогда базовое уравнение преобразуется в следующее:

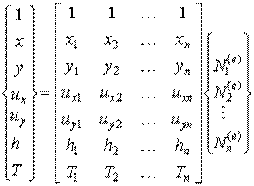
(9.6)

Обратим внимание, что столбец функций формы при данном расширении механических свойств конечного элемента не изменяется. В этом проявляется одно из достоинств изопараметрического подхода – его универсальность.

Линейный изопараметрический треугольный элемент

Рассмотрим типичные изопараметрические конечные элементы, широко используемые в конечно-элементных программах для решения двумерных задач механики. Рассмотренный в предыдущих лекциях линейный треугольный элемент может быть представлен теперь как простейший изопараметрический структурный двумерный элемент, описываемый матричным уравнением:

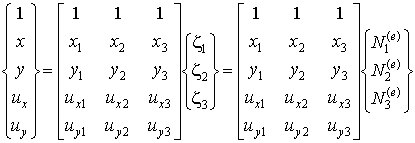
(9.7)

Функции формы выражаются элементарными соотношениями через треугольные координаты:

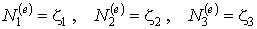
(9.8)

Его вид показан на рис. 9.2.

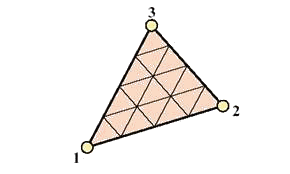
Рис. 9.2. Трехузловой линейный изопараметрический треугольный элемент.

Квадратичный изопараметрический треугольный элемент

Рисунок 9.3 представляет шести узловой треугольный элемент, также являющийся типичным представителем семейства изопараметрических конечный элементов, широко применяющихся в расчетах. Он описывается следующим матричным уравнением:

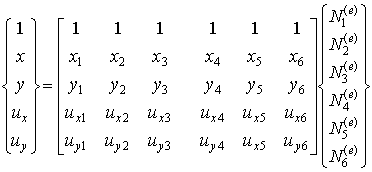
(9.9)

Данный элемент имеет по одному дополнительному узлу на каждой стороне треугольника, что приводит к возможности более точного описания криволинейной границы тела, а также повышает степень аппроксимации перемещений. Последнее свойство достигается тем, что в данном случае используются функции формы в виде полиномов второго порядка:

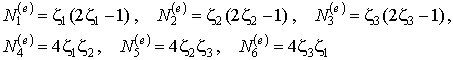
(9.10)

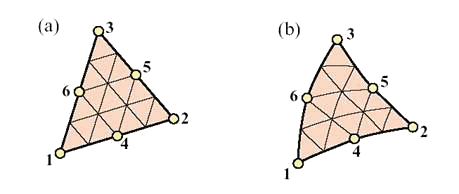
Рис. 9.3. Шести узловой треугольный конечный элемент: (а) – суперпараметрический вариант элемента, имеющий прямолинейные стороны и средние узлы 4, 5, 6, расположенные посередине соответствующих сторон элемента; (б) – изопараметрический вариант того же элемента.

Как показано на рис. 9.3 данный тип элемента имеет две модификации, определяемые расположением средних узлов 4, 5, 6. Первый вариант - суперпараметрический конечный элемент, имеющий прямолинейные стороны и средние узлы 4, 5, 6, расположенные посередине соответствующих сторон элемента 1, 2, 3; (б) – изопараметрический вариант того же элемента. Во втором случае и геометрия, и перемещения заданы полиномами второго порядка. Отсюда и название элемента – квадратичный конечный элемент. В литературе встречается также другое определение - параболический конечный элемент.

Одномерный квадратичный изопараметрический элемент

В первой части курса был рассмотрен простейший конечный элемент – двух узловой линейный элемент – широко применяющийся при решении одномерных задач теории упругости (растяжения и кручения стержней). Сейчас мы можем определить этот элемент как одномерный изопараметрический линейный конечный элемент.

Используя рассмотренную методику, мы можем теперь легко построить изопараметрический элемент более высокого порядка. В частности, в частности при расчетах стержневых систем применяется также одномерный изопараметрический квадратичный конечный элемент.

Пусть имеется трех узловой стержневой элемент. Введем в рассмотрение естественную локальную координату 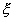. Два концевых узла и один средний пронумеруем в локальной системе координат как 1, 2 и 3 (локальные номера узлов на элементе). Пусть естественные координаты узлов 1, 2 и 3 на элементе равны соответственно:

.

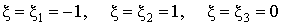Пусть значения функций формы в узлах элемента равны либо нулю, либо единицы:

,

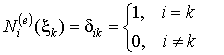(9.11)

где 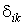- символ Кронекера.

Тогда функции формы могут быть представлены в виде финитных параболических функций следующим образом (Рис. 9.4):

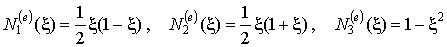
(9.12)

Рис. 9.4. Функции формы стержневого квадратичного изопараметрического элемента. Средние узлы выбраны посередине элемента, однако, в общем случае они могут быть сдвинуты на некоторое расстояние.

Окончательно, определим интерполяционное соотношение для нового элемента следующим образом:

,

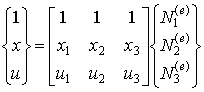(9.13)

где x – глобальная координата элемента (стержня), u – перемещение точек элемента (стержня).

Таким образом, базовые определяющие уравнения элемента построены.

Контрольные вопросы

1. Пояснить понятие изопараметрического подхода в МКЭ.

2. Записать основные интерполирующие соотношения треугольного изопараметрического элемента.

3. Дать понятие квадратичного изопараметрического треугольного элемента. Записать его базовые соотношения.

Лекция 10

Четырехсторонние двумерные элементы