Естественные координаты элемента 2 страница

Численное интегрирование

Полученные выражения (12.9) должны быть проинтегрированы согласно формуле (12.6). Очевидно, что подынтегральные функции могут быть представлены как функции локальных естественных координат элемента согласно формулам (9.3, лекция 9) и (11.13, лекция 11):

(12.10)

Интеграл (12.10) есть интеграл по плоской замкнутой области. Для его вычисления применим известную математическую процедуру. Рассмотрим произвольный элемент е одновременно в локальной и глобальной системах координат. Выделим бесконечно малый элемент площади конечного элемента 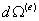(Рис. 12.1).

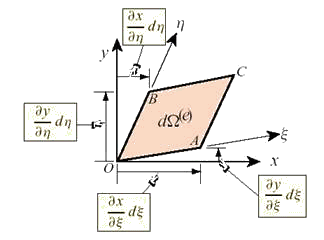
Рис. 12.1. Бесконечно малый элемент площади конечного элемента 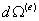в локальной и глобальной системах координат.

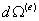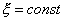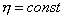Элемент площади образован сторонами ОА и ОВ параллелограмма ОАСВ (Рис. 12.1), которые в свою очередь совпадают с координатными линиями и (см. рис. 10.1, лекция 10). Пусть радиус-вектор вершины параллелограмма точки О имеет радиус вектор:

(12.11)

Рассмотрим изменение этого вектора вдоль координатной линии 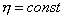, определяемую бесконечно малым изменением аргумента . Получим радиус-вектор вершины А:

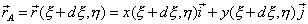
(12.12)

Заметим также, что имеет место очевидное геометрическое соотношение:

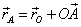
(12.13)

Разложим радиус-вектор точки А (12.12) в ряд Тейлора относительно точки О:

(12.14)

Сравнивая соотношения (12.13) и (12.14), найдем с точностью до величин второго и высшего порядка малости вектор, определяющий сторону параллелограмма ОА:

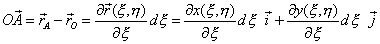
(12.15)

Аналогично рассуждая, найдем вектор, определяющий смежную сторону параллелограмма ОВ:

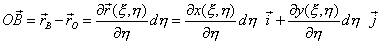
(12.16)

Вычислим теперь площадь параллелограмма 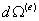, воспользовавшись тем свойством векторного произведения, что его модуль равен площади параллелограмма, образованного векторами, входящими в произведение:

(12.17)

Воспользуемся еще одним свойством векторного произведения, а именно, что оно может быть вычислено с помощью символического определителя:

,

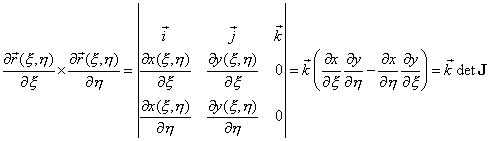(12.18)

где - определитель матрицы Якоби – якобиан, рассмотренный в предыдущей лекции (11.12, лекция 11).

Таким образом, окончательно находим:

(12.19)

С помощью полученного выражения (12.19) можно перейти от интеграла по области к повторному интегралу по локальным координатам в выражении блочных компонент матрицы жесткости (12.10):

(12.20)

Применим известные формулы интегрирования Гаусса для вычисления полученных интегралов. Согласно квадратурам Гаусса, одномерный интеграл от произвольной функции на интервале от -1 до +1 вычисляется следующим образом:

,

(12.21)

где 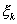- координаты гауссовых точек (узлов квадратуры);

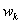- весовые коэффициенты квадратуры;

р – порядок квадратуры.

На рис. 12.2 схематично показаны четыре квадратурные схемы Гаусса соответственно 1-го, 2-го, 3-го и 4-го порядков.

Рис. 12.2. Четыре квадратурные схемы Гаусса порядка р =1, 2, 3, 4. Гауссовы точки показаны черным цветов. Радиусы точек пропорциональны весовым коэффициентам квадратур.

Формула (12.21) легко распространяется на двумерный интеграл. Ее применение к вычислению интегралов (12.20) дает следующее окончательное алгоритмическое выражение для вычисления компонент матрицы жесткости:

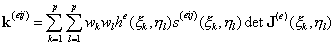
(12.22)

Расположение точек Гаусса на элементе схематично показано на рис. 12.3 для четырех низших квадратур.

Рис. 12.3. Низшие квадратурные схемы Гаусса порядка р = 1, 2, 3, 4 для четырехстороннего элемента. Гауссовы точки показаны черным цветов. Радиусы точек пропорциональны весовым коэффициентам квадратур.

Контрольные вопросы

1. Структура матрицы жесткости изопараметрического четырехстороннего конечного элемента.

2. Вычисление элемента площади изопараметрического четырехстороннего конечного элемента.

3. Как вычисляются интегралы, входящие в матрицу жесткости изопараметрического четырехстороннего конечного элемента?

Лекция 13

Формирование векторов узловых сил изопараметрического элемента

Введение

В настоящей лекции будет подробно рассмотрен алгоритм формирования элементного вектора узловых сил, статически эквивалентного заданным объемным силам (6.27, лекция 6), и элементного вектора узловых сил, статически эквивалентного заданным поверхностным силам 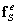(6.28, лекция 6):

	(13.1)
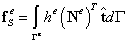
	(13.2)

где - заданный вектор объемных сил;

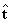- заданный вектор поверхностных сил;

- толщина элемента е;

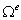- площадь элемента е;

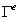- граница элемента е;

- матрица интерполирующих функций, или функций формы элемента.

Структура элементных векторов сил

Рассмотрим структуру выражений (13.1) и (13.2). Аналогично предыдущей лекции все определяется подынтегральным выражением, которое имеет сходную форму для обоих типов элементных векторов. Поэтому достаточно подробно рассмотреть только одно из них, например (13.1).

Раскроем подынтегральное произведение (формулы (5.6, лекции 5) и (4.5в, лекции 4)):

(13.3)

Подставляя полученный матричный вектор (13.3), в формулу (13.1) получим выражение элементного вектора узловых сил, статически эквивалентного заданным объемным силам:

,

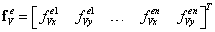(13.4)

где компоненты вектора имеют вид:

(13.5)

Аналогично рассуждая, найдем выражение элементного вектора узловых сил, статически эквивалентного заданным поверхностным силам:

,

(13.6)

где компоненты вектора 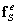имеют вид:

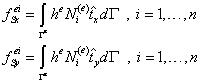
(13.7)

Вычисление компонент элементного вектора объемных сил

Компоненты элементного вектора объемных сил (13.5) вычисляются путем перехода к повторному интегралу аналогично вычислению элементных матриц жесткости, подробно рассмотренному в лекции 12:

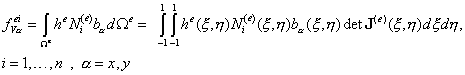
(13.8)

Применения к (13.8) квадратуры Гаусса, в результате получим окончательное выражение для вычисления компонент элементного вектора объемных сил:

(13.9)

Заметим, что как толщина элемента, так и вектор объемных сил также могут быть заданы с помощью изопараметрических соотношений через свои узловые значения:

,

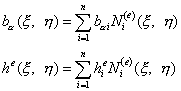(13.9а)

где 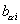- значение заданной силы в узле i конечного элемента;

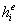- значение толщины элемента е в узле i.

Это особенно удобно при разработке универсальных программных комплексов для унификации ввода данных.

Вычисление компонент элементного вектора поверхностных сил

Вычисление компонент элементного вектора поверхностных сил (13.7) значительно отличается от вычисления интегралов от объемных сил ввиду того, что необходимо интегрировать по границе элемента 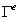. Границей плоской области является кривая линия на плоскости. В данном случае границей области элемента 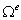будут четыре его стороны. Следовательно, в самом общем случае, который чаще всего не реализован на практике, необходимо вычисление интегралов по каждой из сторон элемента:

,

(13.10)

где 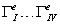- стороны элемента е.

Не умаляя общности, достаточно рассмотреть вычисление лишь одного из интегралов, входящих в сумму (13.10). Возьмем для определенности интеграл по первой стороне четырехстороннего изопараметрического элемента (Рис. 13.1).

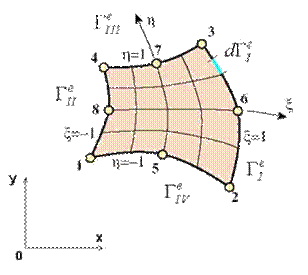
Рис. 13.1. Граница 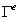четырехстороннего конечного элемента, образованная четырьмя сторонами, и бесконечно малый элемент дуги .

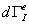Как уже было отмечено, стороны элемента, по определению, совпадают с координатными линиями локальной естественной системы координат (см. лекцию 10): 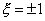и 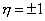. Следовательно, параметрическое представление кривой 2-3, совпадающей с первой стороной элемента и описываемой уравнением 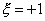в локальной системе координат, имеет вид:

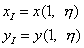
(13.11)

Принимая во внимание изопараметрические соотношения (10.2, лекция 10), уравнение первой стороны элемента виде может быть представлено следующим образом:

(13.12)

Вычислим теперь дифференциал дуги 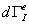, имеющий математический смысл длины бесконечно малого элемента кривой 2-3. С точностью до величин второго и высших порядков малости, элемент 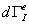является отрезком прямой линии в плоскости , длина которого находится из простого тригонометрического соотношения как гипотенуза прямоугольного треугольника:

,

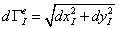(13.13)

где 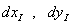- проекции отрезка 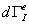на оси глобальной системы координат, они же дифференциалы координат кривой линии 2-3, заданной в параметрическом виде (13.12).

Дифференцируя уравнения (13.12) и подставляя найденные значения 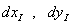в (13.13), получим выражение дифференциал дуги :

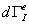(13.14)

Ведем обозначение функции:

,

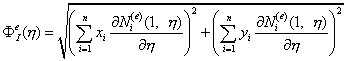(13.15)

имеющей смысл якобиана преобразования между координатами точек кривой, заданной в локальной системе координат уравнением 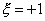, и в глобальной системе координат уравнением (13.12). Другая, но близкая по сути, интерпретация функции (13.15) – якобиан отображения кривой 2-3 на отрезок прямой .

После того, как получено выражение дифференциал дуги 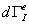, можно перейти от криволинейного интеграла по стороне элемента 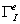к обыкновенному определенному интегралу от функций, зависящих от одной скалярной переменной.:

(13.16)

Численное интегрирование

Применения к (13.16) квадратуры Гаусса, в результате получим окончательное выражение для вычисления компонент элементного вектора поверхностных сил, заданных на первой стороне конечного элемента:

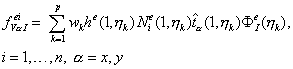
(13.17)

Заметим, что вектор поверхностных сил может быть задан с помощью аналогичных изопараметрических соотношений через свои узловые значения. Однако, в этом случае необходимо использовать одномерные функции формы:

,

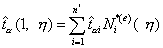(13.17а)

где - значение заданной силы в узле i конечного элемента;

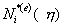- одномерные функции формы;

n^* - число узлов на стороне конечного элемента.

Аналогично вычисляются остальные интегралы, входящие в общее выражение элементного вектора узловых поверхностных сил (13.10). Приведем эти формулы без вывода для полноты изложения (см. рис. 13.1 для пояснения используемой нумерации сторон конечного элемента):

Сторона II, узлы 4-1, уравнение :

(13.18)

Сторона III, узлы 3-4, уравнение :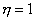

(13.19)

Сторона IV, узлы 1-2, уравнение :

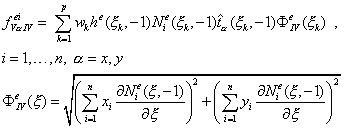
(13.20)

Таким образом, можно сделать вывод, что сформированы все необходимые элементные вектора заданных объемных и поверхностных сил, а также элементные матрицы жесткости. Как правило, это является одним из самых сложных этапов при разработке программной реализации метода конечных элементов. Вторым важным этапом будет сборка глобальных матриц жесткости и векторов нагрузки, формирование системы линейных алгебраических уравнений и решение СЛАУ.

Контрольные вопросы

1. Как вычисляется формирования элементный вектор узловых сил, статически эквивалентного заданным объемным силам.

2. Как вычисляется дифференциал дуги.

3. Как применяется численное интегрирование для вычисления элементного вектора узловых сил, статически эквивалентного заданным поверхностным силам.

Лекция 14

Формирование и решение глобальной системы конечно-элементных уравнений

Введение

В предыдущих лекциях были сформированы все необходимые элементные вектора объемных и поверхностных узловых сил, а также элементные матрицы жесткости. Как правило, это является одним из самых сложных этапов при разработке программной реализации метода конечных элементов. Вторым важным этапом будет сборка глобальных матриц жесткости и векторов нагрузки, формирование системы линейных алгебраических уравнений и решение СЛАУ МКЭ.

Матричное уравнение (6.34, лекция 6) представляет собой стандартную форму записи системы линейных алгебраических уравнений метода конечных элементов (СЛАУ МКЭ):

(14.1)

где K – глобальная матрица жесткости конечно-элементной модели;

U– глобальный вектор степеней свободы (узловых перемещений) модели;

F_V – глобальный вектор узловых сил, статически эквивалентный заданным объемным силам;

F_S – глобальный вектор узловых сил, статически эквивалентный заданным поверхностным силам.

Структура глобальной матрицы жесткости

Матрица жесткости конечно-элементной модели формируется путем сложения по определенным правилам элементных матриц жесткости:

,

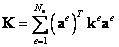(14.2)

где 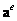- матрицы кинематических связей.

Эта процедура называется сборкой или ансамблированием.

Рассмотрим процесс сборки (14.2) на простом примере, чтобы понять закономерности формирования глобальной системы алгебраических уравнений. Это поможет лучше понять другие более эффективный алгоритмы построения матрицы K, рассматриваемые в специальной литературе по МКЭ.

Пусть сетка образована двумя четырех-узловыми линейными изопараметрическими элементами (Рис. 14.1). Глобальное число узлов равно шести, при этом каждый узел имеет свой уникальный глобальный номер от 1 до 6. Введем локальную естественную систему координат на каждом элементе. Пронумеруем узлы на каждом элементе в соответствии с ориентацией локальной системы координат от 1 до 4. Таким образом, получаем, что каждому узлу ставится в соответствие два номера: локальный 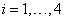и глобальный 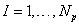, где 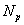- глобальное число узлов конечно-элементной сетки.

Данное соответствие нумерации узлов помогает легко сформировать матрицы кинематических связей 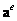, которые, по определению (6.18, лекция 6), связывают глобальный вектор узловых перемещений U с каждым элементным вектором узловых перемещений:

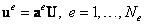
(14.3)

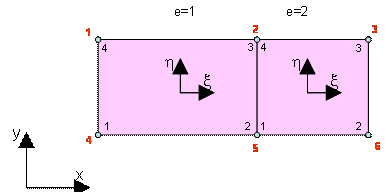
Рис. 14.1. Конечно-элементная сетка, образованная двумя четырех-узловыми линейными изопараметрическими элементами.

Показаны локальные и глобальная системы координат, локальная нумерация узлов на каждом элементе от 1 до 4 и глобальная нумерация по всей сетке от 1 до 6.

В данном случае имеем:

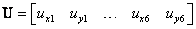,	(14.4)
,	(14.5а)
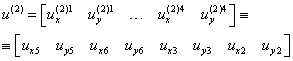.	(14.5б)

Сравнивая выражения (14.5а) и (14.5б) с (14.4) и принимая во внимание, что должны выполняться уравнения (13.3), получим для каждого элемента выражения матриц кинематических связей:

,	(14.6а)
,	(14.6б)

где 1 - единичная матрица размерности 2x2;

0 – нулевая матрица размерности 2x2:

,

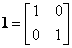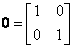
(14.7)

Вычислим первое слагаемое в сумме (14.2):

,

(14.8)

где 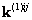- матричный блок размерности 2x2, определяемый формулами (12.9 и 12.22, лекция 12).

Перемножив матрицы в формуле (14.8), получим «отображение» элементной матрицы первого элемента на «плоскость» глобальной матрицы:

(14.9)

Сразу заметим, что положение блока 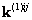в матрице 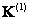определяется соответствующими глобальными номерами. Так, например, блок 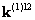имеет локальные номера i=1 и j=2. Узлы с локальными номерами i=1 и j=2 на первом элементе имеют глобальные номера I=4 и J=5. В результате блок 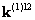перемещается на 4-ю строку, 5-й столбец глобальной матрицы .

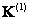Аналогично рассуждая, вычислим второе слагаемое в сумме (14.2):

(14.10)

После перемножения получим:

(14.11)

Остается сложить матрицы (14.9) и (14.11), чтобы получить искомую глобальную матрицу жесткости рассматриваемой конструкции:

(14.12)

Структура глобального вектора узловых сил

Глобальный вектор узловых сил формируется аналогичным образом:

(14.13)

Пусть, например, рассмотренная выше конструкция находится под действием сил тяжести. Тогда будут сформированы два элементных вектора объемных сил в узлах:

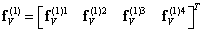,	(14.14а)
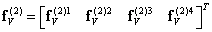,	(14.14б)

где 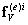- матричный блок размерности 2x1, состоящий из компонент вектора силы в узле i элемента е (13.5, 13.9, лекция 13).

Подставляя выражения (14.14а, б) в (14.13) с учетом вида матриц кинематических связей (14.6а, б), получим глобальный вектор узловых сил:

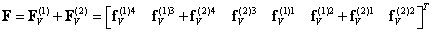
(14.15)

Анализируя выражения (14.12) и (14.15), заметим, что складываются только те элементы матрицы жесткости или вектора нагрузки, которые относятся к общим узлам сетки. Кроме того, если узлы относятся к разным элементам и имеют различные глобальные номера, то соответствующие блоки матрицы жесткости равны нулю. Это является следствием локальности функций формы, благодаря чему имеет место влияние узлов друг на друга только в пределах данного конечного элемента. Влияние же на другие узлы происходит опосредованно через общие узлы между элементами. Это приводит к разреженной структуре глобальной матрицы жесткости с диагональным преобладанием.

Решение глобальной системы конечно-элементных уравнений

После того как глобальная система конечно-элементных уравнений (14.1) сформирована, необходимо разрешить ее относительно глобального вектора степеней свободы модели с тем, чтобы определить все перемещения узлов конструкции. Существует большое количество разработанных методов, алгоритмов и готовых программ для решения систем линейных алгебраических уравнений, наиболее известным из которых является метод исключения Гаусса, состоящий в приведении исходной матрицы к треугольному виду.

Однако при решении и выборе метода расчета систем конечно-элементных уравнений необходимо принимать во внимание ряд свойств СЛАУ и, в частности, свойств матрицы жесткости K:

1. При расчете реальных механических конструкций СЛАУ МКЭ может достигать десятков и сотен тысяч уравнений. Современный рекорд формирования и решения СЛАУ МКЭ равняется 50 миллионам уравнений. Заметим здесь же, что если задача отлична от статической линейной, то необходимое число решений системы может быть сколько угодно большим, например, при расчете динамики конструкции. К счастью, сложности, связанные с большим количеством уравнений, частично компенсируются другими свойствами матрицы жесткости, что и делает МКЭ таким привлекательным с точки зрения инженерных расчетов.