Естественные координаты элемента 4 страница

У каждой программы есть свои сильные и слабые стороны при расчете конкретной конструкции. Выбор программы расчета зависит от подготовленности пользователя в своей научной области, типа решаемой задачи, типа доступной ЭВМ, размерности задачи и других факторов.

К критериям, помогающим сделать выбор, следует отнести следующие факторы:

· программа широко используется;

· в программе используются новейшие научные достижения;

· программа коммерчески вполне доступна;

· имеется подробная и понятная документация.

Ознакомление с программной документацией и доступной литературой с описанием программы и ее элементов позволяют сделать окончательный вывод о целесообразности выбора программного комплекса.

Для МКЭ характерны особенности, которые следует учитывать при выборе и разработке программы расчета. Такими особенностями являются большие объемы исходных данных, промежуточных и окончательных результатов расчета. Поэтому расчет по МКЭ состоит из трех основных этапов:

· разработка расчетной конечно-элементной схемы и подготовка исходных данных;

· проверка самого расчета;

· обработка результатов расчета.

На рис. 17.1. приводится одна из возможных схем организации расчета по МКЭ [33]. Каждый этап является самостоятельной задачей. На первом этапе самое существенное заключается в создании начальной конечно-элементной расчетной модели, исходя из инженерной интуиции о поведении конструкции. В последствии эта модель может корректироваться на основе анализа результатов расчета. Корректировка модели может выполняться и программным путем, если такая возможность реализована в используемом программном комплексе. Подготовка исходных данных осуществляется, как правило, с помощью программ генераторов сеток конечных элементов, образующих блок подготовки данных.

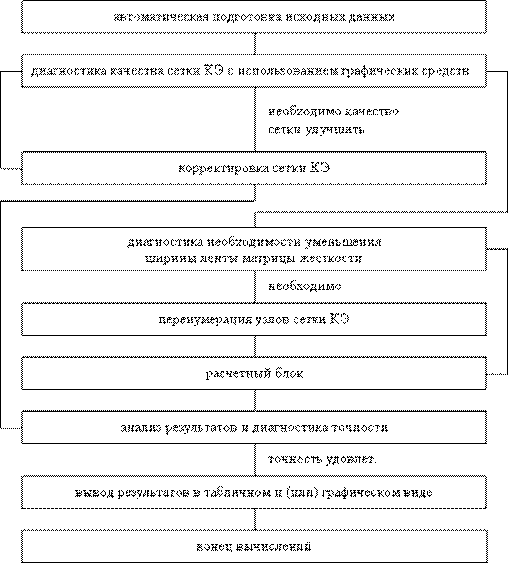
Рис. 17.1. Схема организации расчета по МКЭ.

Проведение расчета (этап 2) осуществляется расчетным блоком, в котором используется тот или иной алгоритм расчета методом конечных элементов. Как правило, расчетный блок состоит из ряда программных модулей, каждый из которых выполняется на определенном шаге алгоритма. В простейшем случае программной реализации МКЭ для линейной статической краевой задачи теории упругости расчетный блок содержит следующую последовательность шагов:

 ввод исходных данных (например, подготовленных программой-генератором в отдельном файле);

 вычисление матриц жесткостей конечных элементов;

 формирование глобальной матрицы жесткости полной структуры;

 формирование глобального вектора нагрузок;

 решение системы линейных алгебраических уравнений;

 вычисление перемещений узлов сетки конечных элементов, деформаций и напряжений в произвольных точках конечных элементах.

На различных шагах расчетного блока включаются проверки правильности исходных данных и результатов промежуточных вычислений (диагностика ошибок), программные модули выбора сочетаний нагрузок, действующих на конструкцию, определение площади сечений арматуры в железобетонных конструкциях и другие. Диагностика ошибок на этапе выполнения программы является важной, так как при своевременном обнаружении ошибки прекращаются вычисления, что приводит к экономному использованию ресурсов ЭВМ.

Эффективное использование ЭВМ достигается также за счет разработки специальных методов решения стандартных математических задач, учитывающих специфику МКЭ, и, в первую очередь, ленточность и разреженность матрицы жесткости расчетной модели конструкции.

Расчет напряженно-деформированного состояния конструкции в рамках линейной теории упругости при действии на нее статических нагрузок сводится к решению системы линейных алгебраических уравнений. В конечно-элементных комплексах программ используются разнообразные методы решения больших систем уравнений.

Различные варианты метода Гаусса реализованы в программах ADINA (блочный метод Гаусса), ASKS, SAP-7 (ленточный метод Гаусса), NASTRAN (L^TDL - декомпозиция). Эффективным является фронтальный метод, реализованный в программах ABAQUS, ANSYS и др. Методы суперэлементов и редукции базиса позволяют существенно сократить время вычисления [18]. Эффективными являются также итерационные методы [1].

Расчет собственных колебаний конструкции выполняется методами: итерации в подпространстве (SAP-7), вычисления корней характеристического определителя (NASTRAN), Хаусхолдера с использованием метода Якоби (ASKA), Гивенса и QR-метода (NASTRAN), Hiber-Hughes (ABAQUS), Ланцоша (PKM). При расчет динамического отклика используются методы: представления решения в виде суперпозиции форм собственных колебаний, шаговые – Вилсона, Ньюмарка (ABAQUS, ADINA, SAP-7, NASTRAN). Решение геометрически и физически нелинейных задач осуществляется, как правило, итерационными методами, основу которых составляет метод Ньютона-Рафсона в сочетании с шаговыми методами (ABAQUS, ADINA, NASTRAN, ANSYS, LASTRAN и др.) [33].

Следует отметить, что принцип модульности программирования, использованный в программных комплексах, позволяет создавать как универсальные вычислительные программы, так и промышленные для решения узкого класса задач. На первых этапах освоения МКЭ разрабатывались в основном промышленные вычислительные программы. Они эффективны, если решается большое количество вариантов однотипных задач, либо выполняется большой объем вычислений для качественного и количественного исследования явлений, связанных с новой постановкой задачи. Тенденция развития вычислительной техники, приведшая к созданию персональных ЭВМ и новых информационных технологий, оказала влияние на разработку программного обеспечения МКЭ [6]. Программные комплексы по МКЭ активно используются в системах автоматизированного проектирования, базирующихся на персональных ЭВМ (AutoCAD/MechanicalDesktop, Pro-Engineer).

Краткие характеристики некоторых программных комплексов

Современные комплексы программ, в которых используется МКЭ, позволяют получать приближенные численные решения при расчете конструкций на статические и динамические нагрузки для широкого класса материалов с различными механическими характеристиками и поведением. Расчет конструкций на статические нагрузки может производиться с учетом физической и геометрической нелинейности, температурных полей, взаимодействия с другими средами (например, с жидкостью). Производится расчет критических нагрузок, при которых конструкция или ее элементы теряют устойчивость, поведения конструкции после потери устойчивости. МКЭ позволяет также определить нагрузки, при которых происходит разрушение конструкции. Учитываются такие свойства материала как анизотропность, нелинейная упругость, пластичность, текучесть. Учитываются виды геометрической нелинейности: большие деформации и большие перемещения. Основными динамическими задачами являются: расчет собственных колебаний конструкции; динамический отклик на нагрузку, зависящую от времени; распространение волн [33].

Ниже в таблице 17.1. приводятся сравнительные характеристики наиболее распространенных комплексов программ описанных в работе [40].

Таблица 17.1. Краткие характеристики наиболее распространенных комплексов программ МКЭ

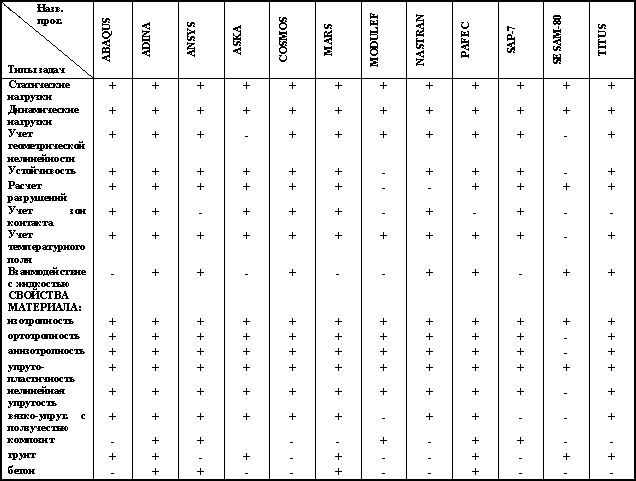
Приведенные в таблице комплексы программ являются универсальными. Опишем подробно один из комплексов, например, ABAQUS [33]. Этот программный комплекс разработан относительно недавно для расчета новых прогрессивных конструкций. Разработчики этого комплекса (Hibbit, Karlson, Sorensen) сохранили простоту и эффективность расчета для линейных задач при учете сугубо нелинейных эффектов – геометрических и физических. Комплекс программ позволяет производить расчет стационарных и нестационарных температурных полей, их влияния на напряженно-деформированное состояние конструкции, ее устойчивость, оценивать трещинообразование, учитывать зоны контакта с трением, учитывать процессы фильтрации жидкости в грунтах. Расчет на нагрузку, зависящую от времени, производится с учетом предварительной нагруженности конструкции. Обширная библиотека конечных элементов, разнообразный набор характеристик материала (линейно упругий, гиперупругий, полностью несжимаемый с зависимостью свойств от температуры) и моделей его поведения (общий упругопластический с изотропным и кинематическим упрочением, упруговязкопластический, специальные законы ползучести, объемное упрочнение) позволяют решать достаточно широкий класс задач.

Следует отметить, что выбор модели поведения материала является определяющим для достоверности рассчитанного напряженно-деформированного состояния конструкции. Например, в программе MARS используется 30 моделей поведения материала (вязкоупругость по Максвеллу или Кельвину; пластичность по критерию Мизеса или Мора, или Кулона, с изотропным или (и) кинематическим упрочением по теории ассоциированного или неассоциированного течения, с учетом температуры; ползучесть по закону Мизеса, чисто объемная или чисто девиаторная ползучесть, анизотропность при упругопластической ползучести: вязкопластичность, несжимаемость или почти несжимаемость, большие деформации по закону Муни-Ривлина и т.д.).

Программы промышленного назначения предназначены для расчета узкого класса конструкций. Примером программы промышленного назначения является программа BERSAFE, разработанная для расчета элементов конструкций атомной энергетики. В этой программной системе для расчета напряженно-деформированного состояния используются специальные законы ползучести бетона и графита, поведения скальной породы. Другим примером программы промышленного назначения служит программа EFESYS, предназначенная для расчета плотин и морских сооружений с учетом связанности процессов фильтрации и напряженно-деформированного состояния. Программный комплекс ПОЛИФЕМ-87 предназначен для расчета на сейсмические воздействия сооружений как пространственных систем. Отметим, что универсальные и промышленные комплексы программ не могут быть эффективно использованы для изучения МКЭ. Для изучения различных аспектов МКЭ разработаны специальные учебные программные комплексы [37]. Для решения различных задач биомеханики широко используются коммерческие универсальные комплексы ABAQUS, ANSYS, MARS, NASTRAN, а также разрабатываются специализированные программы, реализующие метод конечных элементов, для повышения эффективности решения той или иной конкретной задачи [39].

Дополнительная литература

1. Абрамов Н.Н., Беркун В.Б., Кучеренко В.В., Перекальский В.М. Эффективные итерационные алгоритмы решения тепловых задач: Учебное пособие – М.: МИСИ, 1987. 67 с.

2. Басов К.А. ANSYS в примерах и задачах. М.: КомпьютерПресс, 2002. 224 с.

3. Бердичевский В.Л. Вариационные принципы механики сплошной среды. М.: Наука, 1982, 448 с.

4. Боровков А.И. Программный комплекс конечно-элементного анализа FEA // Аннотированный каталог учебных программных средств. Вып.3. СПб: СПбГТУ, 1995. С.100-102.

5. Бреббия К., Телес Ж., Вроубел Л. Методы граничных элементов. М.: Мир, 1987. 348 с.

6. Бурман Я.З., Салахов Р.Р. О реализации МКЭ на персональных ЭВМ. Прикладные проблемы информатики, No1, 1989.

7. Бурышкин М.Л., Гордеев В.Н. Эффективные методы и программы расчета на ЭВМ симметричных конструкций. Киев: Будивельник, 1984.120 с.

8. Бутенин Н.В., Лунц Я.Л., Меркин Д.Р. Аналитическая механика. М.: Наука, 1984. 452с.

9. Васидзу К. Вариационные методы в теории упругости и пластичности. М.: Мир, 1987. 542 с.

10. Вилипыльд Ю.К., Лайгна К.Ю., Кала Т.Н. Расчет стержневых и пластинчатых систем по методу конечных элементов МКЭ/20. Таллинн, 1979. 115 с.

11. Галкин Д.С., Галкина Н.С., Гусак Ю.В. Многоцелевая автоматизированная расчетная система МАРС. Сб.: Комплексы программ математической физики. – Новосибирск, 1984.

12. Галлагер Р. Метод конечных элементов. Основы. М.: Мир, 1984. 428 с.

13. Городецкий А.С. Программа МИРАЖ для статического расчета конструкций методом конечных элементов. Автоматизация проектирования как комплексная проблема совершенствования проектного дела в стране: Сб. трудов всесоюзной научной конференции. М., 1973.

14. Городецкий А.С., Здоренко В.С. Типовая проектирующая подсистема ЛИРА для автоматизированного проектирования несущих строительных конструкций. Сб.: Системы автоматизированного проектирования объектов строительства. Вып.1, 1982.

15. Зенкевич О. Метод конечных элементов в в технике. М.: Мир, 1975. 536 с.

16. Зенкевич О., Морган К. Конечные элементы и аппроксимация. М.: Мир, 1986. 318 с.

17. Исаханов Г.В., Кислоокий В.Н., Сахаров А.С., Синявский А.Л. Система математического обеспечения расчетов пространственных конструкций // Проблемы прочности, No11, No12, 1978.

18. Калугин О.Ю., Кучеренко В.В., Попов В.А., Щукин О.И. Методика использования макроэлементов для решения на ЭВМ пространственных задач большой размерности. Учебное пособие. – М.: МИСИ, 1987. 105 с.

19. Лехницкий С.Г. Теория упругости анизотропного тела. М.: Наука, 1977. 282 с.

20. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики. Т. 1, 2. М.: Наука, 1982, 1983. 352 с., 640 с.

21. Лурье А.И. Теория упругости. М.: Наука, 1980. 936 с.

22. Лурье А.И. Нелинейная теория упругости. М.: Наука, 1980. 512 с.

23. Маслов Л.Б. Пpименение методов гpаничных и конечных элементов для анализа концентpации напpяжений в двумеpных и тpехмеpных задачах теоpии упpугости. Дис. … канд. техн. наук. ЛГТУ, 1992. 258 с.

24. Маслов Л.Б. Численные методы для pешения задач теоpии упpугости: Методическое пособие / Иван. гос. энеpг. ун-т.- Иваново, ИГЭУ, 1999. - 28с.

25. Маслов Л.Б., Козлов М.В. Конечно-элементный программный комплекс “МЕХАНИКА” - приложение в инженерном деле и биомеханике // Вестник Иван. гос. энеpг. ун-та. - Иваново, ИГЭУ, 2002. - No 2. - С. 23-28.

26. Молчанов И.Н., Николенко Л.Д. Основы метода конечных элементов. Киев: Наукова Думка, 1989. 272 с.

27. Никольский М.Д., Чернева И.М., Безперстова Н.Ф.и др. Комплекс программ МОРЕ для расчета сооружений по методу конечных элементов. В книге: Экспериментальные и теоретические исследования по механике твердого деформируемого тела. Сб. трудов ЛИИЖТ. – Л.: ЛИИЖТ, 1978.

28. Постнов В.А. Проблемы автоматизации метода суперэлементов. Программный комплекс КАСКАД-2. Сб.: Применение численных методов в строительной механике. – Л.: Судостроение, 1976.

29. Работнов Ю.Н. Механика деформируемого твердого тела. М.: Наука, 1988. 712 с.

30. Самарский А.А. Введение в численные методы.- М.: Наука, 1987. - 459с

31. Тимошенко С.П., Янг Д.Х., Уивер У. Колебания в инженерном деле. М.: Машиностроение, 1985. 472 с.

32. Флетчер К. Численные методы на основе метода Галеркина. М.: Мир, 1988. 352с.

33. Хечумов Р.А., Кепплер Х., Прокопьев В.И. Применение метода конечных элементов к расчету конструкций. М.: Изд-во Ассоциации строительных вузов, 1994. 353 с.

34. Шапошников Н.Н. Система прочностных расчетов по МКЭ СПРИНТ для ЕС ЭВМ. Сб.: Практическая реализация численных методов расчета инженерных конструкций. – Л.: Знание, 1981.

35. Шимкович Д.А. Расчет конструкций в MSC/NASTRAN for Windows. ДМК, 2001. 448 с.

36. ANSYS Basic Analysis Procedures Guide. 1998.

37. Dahlblom O., Peterson A., Peterson H. CALFEM – a program for computer-aided learning of the finite element metod. Eng.Comput.,vol.3, N02,1986.

38. Felippa C., Introduction to Finite Element Methods, University of Colorado Press, 2002.

39. Middleton, J., Jones, M.L., Eds., Computer Methods in Biomechanics and Biomedical Engineering. Gordon & Breach Science Publishers, 1998.

40. Niku-Lari A. Structural analysis system, (Sofware-Hardware, Capability – Compability – Aplications). Pergamon Press,vol.1-3,1986.

41. Pilkey W., Saczalski K.,Schaeffer H. Structural Mechanics Computer Programs, Surveys, Assessments, and avialability. – Univertsity Press of Virginia,1974.

42. Zienkiewicz O.C., Taylor Robert L., Taylor R.L., Finite Element Method: Volume 1, The Basis. Butterworth-Heinemann, 2000. 712 p.

43. Zienkiewicz O.C., Taylor Robert L., Taylor R.L., Finite Element Method: Volume 2, Solid Mechanics. Butterworth-Heinemann, 2000. 480 p.

Контрольные вопросы

1. Нарисовать схему организации расчета по МКЭ.

2. Основные характеристики современных программных комплексов.

3. Перечислить содержание расчетного блока в алгоритме МКЭ.

Лекция 18

Примеры применения программных средств конечно-элементного анализа

Введение

В лекции рассматривается применение авторского комплекса MechanicsFE и коммерческого универсального пакета ANSYS к решению ряда задач механики.

Исследование напряженного состояния рамы прицепа автомобиля

Целью численного моделирования являлся проверочный статический расчет напряженно-деформированного состояния рамы прицепа легкового автомобиля модели 8190, разработанного и подготовленного к выпуску ООО СП “Родниковское управление предприятий”.

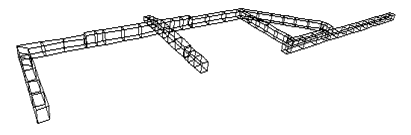
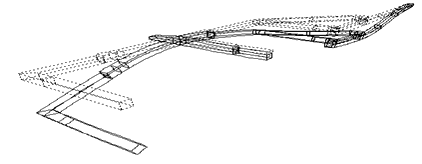
Конечно-элементная модель рамы с учетом симметрии конструкции относительно продольной вертикальной плоскости (XZ) показана на Рис.18.1а. Параметры модели: число элементов N_e=69, число узлов N_p=808. Вид деформированной конструкции под действием полезной нагрузки и сил собственного веса Р=3720 Н показан на Рис.18.1б. Результаты расчетов напряжений представлены на Рис. 18.2. На лонжеронах рамы показаны распределения напряжений 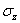, на поперечинах - 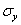, как основных компонент, определяющих напряженное состояние, соответственно, лонжеронов и поперечин. Исходя из максимального значения 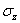=39.4 МПа, характеристик стали 08КГ и условий эксплуатации прицепа, был определен коэффициент запаса прочности, равный 1.48, что можно признать удовлетворительным.

(а)

(б)

Рис. 18.1. Пространственная конечно-элементная модель рамы прицепа легкового автомобиля (а) и деформированная конструкция под действием полезной нагрузки и собственного веса (б).

Приведенные рисунки и графики дают представление об общем характере напряженно-деформированного состояния конструкции. Однако, как правило, любой геометрически сложный механический объект имеет зоны концентрации напряжений, которые не всегда удается выявить в глобальной модели. Поэтому был проведен уточненный расчет в зоне крепления кронштейна дышла прицепа к поперечине с использованием локальной конечно-элементной модели части конструкции (Рис. 18.3а).

Внешняя сила, полученная из результатов расчета напряжений на предыдущем этапе по глобальной модели, была приложена на поверхности отверстия в кронштейне в нормальном направлении. Результаты расчета представлены в виде деформированной конструкции (Рис. 18.3б) и изолиний основных напряжений в плоскости кронштейна (Рис. 18.4).

Проведенный численный анализ свидетельствует о достаточной прочности прицепа. При этом, уровень возникающих напряжений позволяет рассмотреть вопросы повышения грузоподъемности либо увеличения ресурса конструкции, а также возможной оптимизации с точки зрения снижения расхода материала или упрощения технологического процесса изготовления деталей и сборки узлов.

Рис. 18.2. Распределение нормальных напряжений по лонжеронам и поперечинам рамы.

(а)

(б)

Рис. 18.3. Уточненная локальная конечно-элементная модель поперечины с кронштейном рамы прицепа (а) и деформированная конструкция под действием расчетных нагрузок (б).

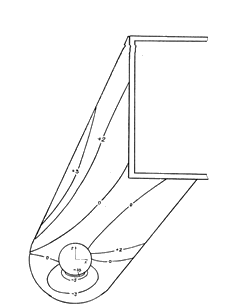
Рис. 18.4. Изолинии напряжений 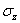(МПа) в плоскости кронштейна.

Конечно-элементный анализ напряженного состояния стрелы экскаватора

Рассмотрена статическая задача анализа напряженно-деформированного состояния стрелы экскаватора, выпускаемого машиностроительной компанией КРАНЕКС г. Иваново (Рис.18.5). Технически стрела представляет из себя коробчатую механическую конструкцию, сваренную из стальных листов и усиленную поперечными ребрами жесткости. Основание стрелы шарнирно закреплено на поворотной площадке экскаватора, а с противоположной стороны шарнирно связано с рабочим звеном и ковшом.

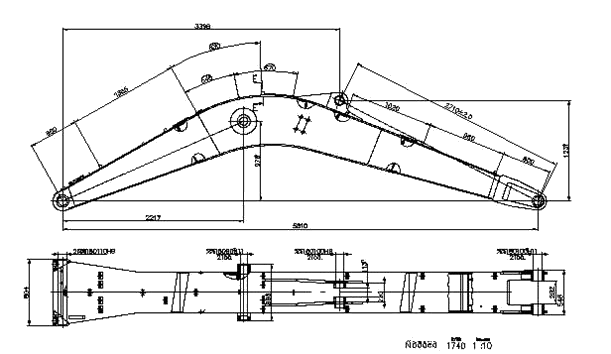
Рис.18.5. Сборочный чертеж стрелы экскаватора

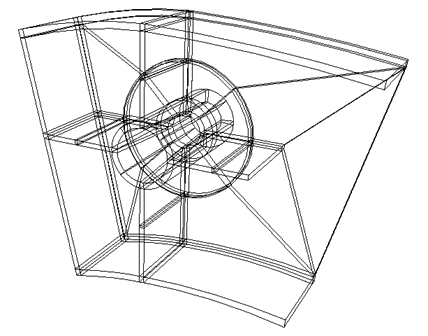
Рис.18.6. Центральный силовой узел стрелы: цапфа гидронасоса с дополнительными ребрами жесткости.

Напряженное состояние стрелы рассчитывалось как результат действия максимальной внешней нагрузки со стороны гидравлических насосов, шарнирно соединенных с проушиной и боковыми цапфами. Подобная постановка задачи моделирует наиболее критическую ситуацию во время эксплуатации экскаватора, которая может возникать при заклинивании ковша в почве. При этом гидравлические насосы работают на полную мощность, создавая максимальные внешние силы, а движения стрелы не происходит. В результате при практическом использовании экскаватора, наблюдаются частые разрушения конструкции в области сопряжения цапфы и боковых листов, выражающиеся в выламывании цапф из стрелы.

Для усиления конструкции в проблемной зоне были введены дополнительные ребра жесткости в двух перпендикулярных плоскостях (Рис.18.6) и новая модификация была пущена в производство. Однако, опыт эксплуатации показал, что проблема прочности исследуемого узла тем не менее осталась. Поэтому было предложено провести численный анализ конструкции в двух вариантах и сравнить полученные результаты.

Модель

В пакете ANSYS разработана пространственная конечно-элементная модель стрелы экскаватора (Рис.18.7) с учетом дополнительных внутренних ребер жесткости вокруг центральных цапф и без них. Поскольку стальные листы, из которых сварена стрела, являются плоскими или имеют малую кривизну при толщине 12 или 16 мм, то для компьютерного моделирования был использован оболочечный изопараметрический конечный элемент с шестью степенями свободы в узле и параболической интерполяцией по перемещениям типа SHELL93. Толщина элементов также учитывалась путем задания соответствующих значений в меню Real constants. При этом пришлось вводить некоторые упрощения реальной конструкции в областях, далеких от исследуемой зоны концентрации напряжений, применяя оболочечные элементы различной толщины.

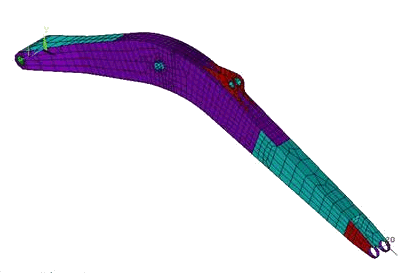
Рис. 18.7. Конечно-элементная оболочечная модель стрелы в базовом варианте

Кинематические граничные условия на цилиндрах слева и справа выбирались таким образом, чтобы моделировать возможность поворота стрелы в шарнирах. Внешние нагрузки представляли собой силы, приложенные в узлах на выбранных поверхностях цапф и проушины в заданном направлении. Согласно техническому заданию на цапфы действует суммарная сила величиной 943 кН под углом 38⁰ к продольной оси X, соединяющей центры левого и правого шарнира стрелы, к проушине приложена сила 193 кН под углом 169⁰ к оси.

Тем самым, с точки зрения обыкновенной теории изгиба стержней стрела представляет собой искривленную шарнирно опертую балку. Однако, решение задачи методами сопротивления материалов не может дать представления о концентрации напряжений в зоне перехода цапфы - боковые листы, что приводит к необходимости решения задачи в трехмерной постановке методами механики деформируемого тела.

Результаты

Был проведен статический прочностной расчет численной модели стрелы в двух вариантах - с учетом дополнительных ребер жесткости и без них.

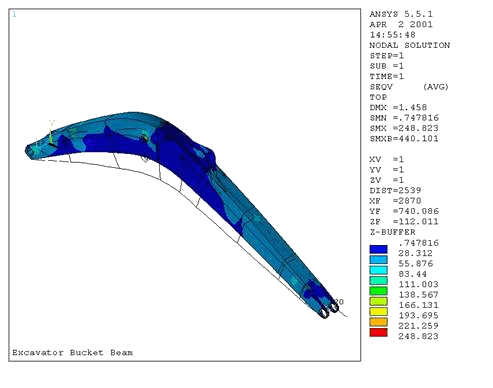
Анализ перемещений показал наличие больших деформаций в районе приложения сил, а также значительный прогиб стрелы в вертикальном направлении как шарнирно-опертой балки. Наблюдается значительное искривление цапфы и выгибание стальных листов в зоне крепления проушины (Рис.18.8).

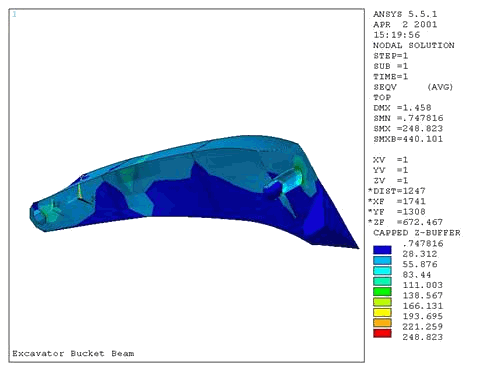
Статический анализ напряжений показал, что общее напряженно-деформированное состояние стрелы сходно с напряженным состоянием шарнирно-опертой балки. При этом наибольшие напряжения не превышают 50 МПа. Однако, в зоне сопряжения цапфы и боковых листов наблюдается значительная концентрация напряжений, в несколько раз превышающая уровень напряжений, рассчитанный по теории изгиба балок (Рис.18.9).

(а)

(б)

Рис. 18.8. Деформированная модель стрелы в базовом варианте и распределение эквивалентных напряжений по Мизесу (а). Распределение напряжений в зоне сопряжения цапфы и боковых листов стрелы (б).

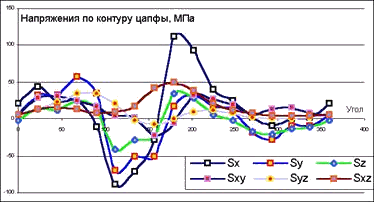
Рис. 18.9. Распределение напряжений в зоне сопряжения цапфы и боковых листов стрелы по окружности цапфы

Сравнительный анализ напряженно-деформированного состояния усиленной стрелы с базовым вариантом показал, что введенные дополнительные ребра жесткости не влияют принципиально на распределение напряжений в стреле (Рис.18.10). В ходе дальнейшего обсуждения полученных результатов с представителями машиностроительной компании, инженеры технического центра согласились с нашими выводами о необходимости других конструктивных решений данного узла.

Заключение

Проведенный конечно-элементный анализ напряженно-деформированного состояния стрелы экскаватора подтвердил наличие опасной зоны в центральном силовом узле стрелы с точки зрения возможных разрушений. Разработанная численная модель может быть использована для дальнейшего исследования различных технических вариантов усиления конструкции в зоне концентрации напряжений.

(a)

(б)

Рис. 18.10. Деформированная модель стрелы в усиленном варианте и распределение эквивалентных напряжений по Мизесу (а). Распределение напряжений в зоне сопряжения цапфы и боковых листов стрелы (б)

Контрольные вопросы

1. Основные задачи инженера при расчете конструкций.

2. Для чего используется локальная модель подконструкции?

3. Что такое предел прочности и как он связан с результатами расчета методом конечных элементов?

Лекция 19

Теоретические основы метода граничных элементов

Введение

Численные методы механики деформируемого твердого тела могут быть разделены на три основных вида: метод конечных разностей, метод конечных элементов и метод граничных элементов (более общее название – метод граничных интегральных уравнений).

Первый из этих методов связан с непосредственной реализацией разностного оператора, соответствующего исходному дифференциальному уравнению задачи. Данный подход обладает одним существенным свойством: он позволяет легко распространить методику на решение нелинейных задач и не требует сложных математических преобразований. К сожалению, точность получаемых результатов оказывается невысокой.

Метод конечных элементов базируется на разбиении исследуемого тела на ряд подобластей простого очертания, называемых конечными элементами. В основе численной модели лежат вариационные принципы механики, наиболее часто принцип минимума потенциальной энергии. Механическая ясность и широкие практические возможности метода объясняют его популярность среди исследователей.

Однако существует много классов задач, для которых конечно-элементная реализация неудовлетворительна, что и заставило ученых обратиться к альтернативным методам, основывающимся на интегральных уравнениях.

В данном курсе лекций мы рассмотрим один из таких подходов – прямой метод граничных элементов. Сначала изложим математическую базу метода: исходная система дифференциальных уравнений пространственной задачи теории упругости преобразуется в граничное интегральное уравнение относительно неизвестных поверхностных перемещений и напряжений. Для численного решения этого уравнения вся поверхность тела разбивается на ряд элементов, в пределах которых перемещения и напряжения интерполируются с помощью полимиальных функций через их значения в узловых точках. Далее опишем программы для численного решения плоских задач теории упругости и рассмотрим тестовый пример на применение данной программы.