Естественные координаты элемента 6 страница

,

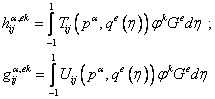(21.5)

где вид ядер 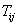, 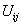задан выражениями (20.9, лекция 20).

Рис. 21.1. Граница области с угловой точкой.

Матрицы 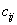для любой точки 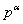имеют простой вид:

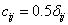
в том случае, если граница в окрестности точки 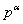гладкая.

Если точка 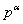угловая, то выражение матрицы 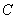имеет вид:

,

где , - углы, показанные на рис. 21.1.

Таким образом, на данном этапе, являющемся наиболее сложным, вычисляются интегралы (21.5) и формируется СЛАУ (21.4). После наложения граничных условий (19.1а, лекция 19), т.е. разбивки глобальных векторов 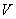и 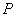на известную часть 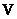, 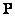и неизвестную часть 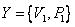, СЛАУ (21.4) преобразуется к стандартному виду (20.7, лекция 20).

Четвертый этап – решение СЛАУ МГЭ.

Для решения системы линейных алгебраических уравнений используются стандартные численные методы. Наиболее распространены метод неизвестных Гаусса и итерационные методы. Выбор того или иного метода зависит от конкретных размеров матрицы 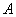и возможностей вычислительной техники.

Отметим две важные особенности СЛАУ МГЭ. Во-первых, матрица является полностью заполненной и несимметричной. В этом состоит ее существенный недостаток и отличие от глобальной матрицы жесткости МКЭ, которая является разрешенной (т.е. с большим количеством нулевых элементов) и симметричной, что позволяет использовать более эффективные численные методы решения СЛАУ. Вторая особенность матрицы 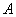состоит в том, что ее размер значительно меньше размера матрицы жесткости МКЭ, что существенно компенсирует отмеченные недостатки. Данная черта матрицы 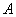объясняется тем, что в МГЭ неизвестными являются перемещения и усилия в узлах границы 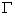, в то время как МКЭ требует разбиения всей области 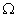на конечные элементы. Следовательно, вектор неизвестных, определяющий размер матрицы СЛАУ, содержит значения перемещений (или сил) во всех узлах области 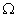, число которых много больше граничных узлов.

После решения СЛАУ (20.7, лекция 20) глобальные векторы перемещений 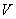и усилий 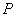будут полностью определены во всех узлах границы 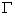. Следовательно, зная узловые значения граничных элементов, можно вычислить перемещения и усилия так же в любой точке 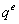границы согласно интерполяционным соотношениям (20.2, лекция 20).

Пятый этап – определение граничных напряжений.

В плоской задаче теории упругости основными неизвестными напряжениями являются:

.

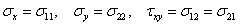Напряжение 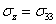в случае плоского напряженного состояния равно нулю, в случае плоского деформированного состояния вычисляется через основные напряжения следующим образом:

.

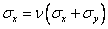Напряжения 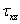и 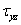равны нулю в обоих вариантах плоской задачи теории упругости.

Согласно граничным условиям

.

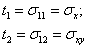Другими словами, два из трех основных напряжений определяются в ходе решения СЛАУ на четвертом этапе.

Для вычисления напряжения 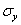необходимо воспользоваться законом Гука:

,

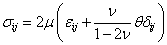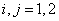
(21.6)

и кинематическими соотношениями, связывающими между собой перемещения и деформации:

, .

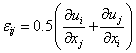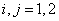(21.7)

Так как после решения СЛАУ (20.7, лекция 20) вектор перемещения оказывается известным, то можно осуществить численное дифференцирование согласно формуле (21.7) и использовать закон Гука (21.6) для вычисления .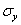

Шестой этап – вывод результатов.

Выходная информация содержит основные сведения о гранично-элементной модели задачи (число макроэлементов, число граничных элементов, число узлов, число степеней свободы дискретной системы), тип плоского состояния (плоское напряженное или плоское деформированное), характеристики глобальной системы линейных алгебраических уравнений, результаты расчета (глобальные номера узлов и граничных элементов, значения перемещений, усилий и напряжений в узлах гранично-элементной сетки). Для вычисления полей перемещений и напряжений во внутренних точках области 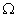используется тождество Сомильяны. Данная процедура не требует решения системы уравнений, поскольку граничные перемещения уже известны, а тождество Сомильяны осуществляет связь между граничными перемещениями во внутренних точках области.

Пример применения метода граничных элементов

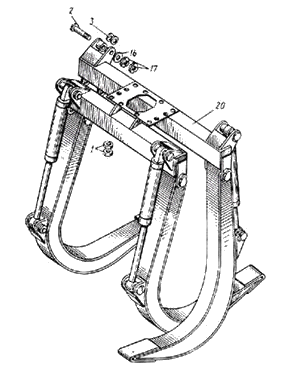
Рассмотрим анализ напряженно-деформированного состояния детали механической конструкции - челюсти грейфера-захвата для древесины, выпускаемого компанией КРАНЕКС (г. Иваново). Требуется исследовать напряженно-деформированное состояние челюсти грейфера-захвата для древесины (Рис.21.2), определить опасные сечения, зоны концентрации напряжений, максимальные напряжения. Действующая нагрузка - вес поднимаемого груза, распределенного равномерно по небольшой площадке челюсти грейфер, равный 10 Н/мм. Рассматривается задача в статической линейной постановке в предположении реализации в исследуемой детали плоско-напряженного состояния. Для решения возникающей двумерной задачи теории упругости применен метод граничных элементов, реализованный в виде программы BPS, входящего в авторский программный комплекс MechanicsFE.

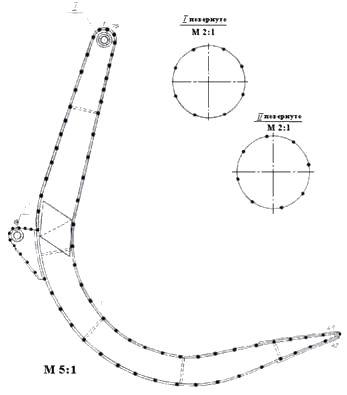
Рис. 21.2. Конструкция грейфера и гранично-элементная модель челюсти захвата.

Первоначально разрабатывается так называемая макроэлементная модель конструкции, для чего определяются координаты характерных точек на поверхности, описывающих геометрию упругой области в целом. Число макроэлементов выбирается минимально возможным для наиболее точного описания границы тела. Затем с помощью специальной программы, называемой автоматическим генератором сетки, макроэлементы разбиваются на более мелкие граничные элементы. Тем самым формируется окончательная компьютерная модель конструкции (Рис.21.2).

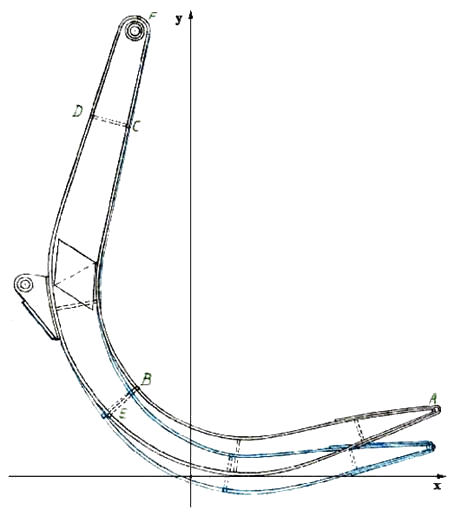
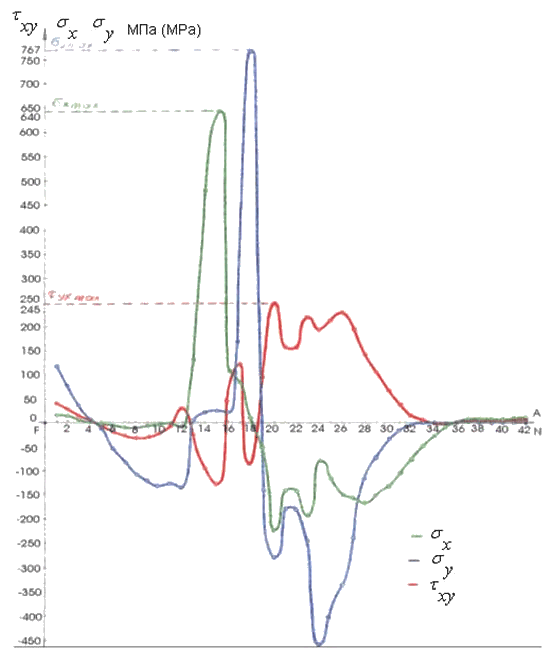
На рис. 21.3 представлены результаты расчета задачи на выбранной сетки. Рисунок деформированной конструкции соответствует тому, что подсказывает здравый смысл - основная несущая часть челюсти грейфера изгибается под действием веса полезного груза. Наибольшие напряжения на внутренней границе тела возникают в зоне перехода от горизонтального участка челюсти к вертикальному, что соответствует теории изгиба консольного стержня. Однако, максимальные напряжения локализуются в небольшой области вблизи выносной детали челюсти, предназначенной для шарнирного крепления подъемной тяги. Это говорит о концентрации напряжений в указанной зоне и, хотя предел прочности для данного вида стали не превышен при рассмотренной нагрузке на одну челюсть, требуется повышенное внимание к данному элементу конструкции в процессе эксплуатации (более частые профилактические осмотры, специальные методы диагностики, особенно на зарождение и распространение трещин). Необходимо дальнейшее исследование математической модели конструкции с целью оптимизации формы соединения деталей челюсти и минимизации возникающих напряжений.

На этом примере мы заканчиваем знакомится с учебной дисциплиной “Вычислительная механика”. Надеемся, что приведенные теоретические изложения и примеры не оставляют сомнения в высокой эффективности численных методов для решения инженерных задач, а также в необходимости их углубленного изучения и развития.

Рис. 21.3. Деформированное состояние конструкции и распределение напряжений по внешней стороне челюсти захвата.

Контрольные вопросы

1. Перечислить основные шаги алгоритма МГЭ.

2. Назвать свойства глобальной матрицы СЛАУ МГЭ.

3. Пояснить особенности вычисления напряжений на границе области в методе граничных элементов.

Список необходимых понятий на момент начала изучения рассматриваемого курса

Сложная функция многих переменных, дифференциал, частная производная, интеграл по кривой, по области и по объему, повторный интеграл, вектор, тензор, матрица, скалярное и векторное произведение, транспонированная и обратная матрица, радиус-вектор, вектор перемещений, вектор силы, сосредоточенные и распределенные силы, тензор деформаций и напряжений, потенциальная энергия упругого тела, работа силы, вариация функции, функционал, вариационный принцип, гармонические колебания, обобщенные координаты и степени свободы.