Естественные координаты элемента 5 страница
В лекциях будем использовать декартовое тензорное обозначение, в соответствии с которым для представления осей (x, y, z) используются индексы (1, 2, 3). Кроме того, необязательны символы суммирования, если в слагаемом одни и те же нижние индексы встречаются дважды. Например,
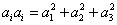 ,
,
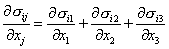 .
.
В данной лекции будет показано, как задача теории упругости, сформулированная в идее полной системы уравнений линейной теории упругости с граничными условиями, может быть сведена к интегральному уравнению, допускающую численную реализацию в рамках прямого метода граничных элементов.
Постановка пространственной задачи теории упругости
Рассмотрим тело 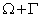 (
( 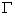 - граница области
- граница области 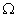 ) (Рис. 19.1), которое находится в состоянии равновесия под воздействием заданных нагрузок и перемещений. Это состояние описывается полной системой уравнений линейной теории упругости:
) (Рис. 19.1), которое находится в состоянии равновесия под воздействием заданных нагрузок и перемещений. Это состояние описывается полной системой уравнений линейной теории упругости:
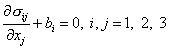 , ,
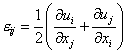 , ,
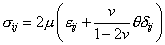 , ,
| (19.1) |
где
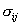 - компоненты тензора напряжений;
- компоненты тензора напряжений;
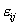 - компоненты тензора деформаций;
- компоненты тензора деформаций;
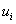 - компоненты вектора перемещений;
- компоненты вектора перемещений;
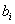 - компоненты вектора объемных сил;
- компоненты вектора объемных сил;
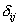 - символ Кронекера,
- символ Кронекера, 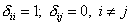 ;
;
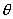 - объемная деформация,
- объемная деформация, 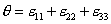 ;
;
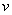 - коэффициент Пуассона;
- коэффициент Пуассона;
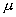 - модуль сдвига.
- модуль сдвига.
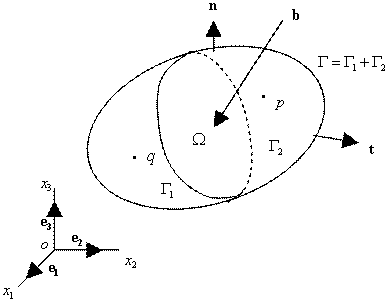
Рис. 19.1. Постановка пространственной задачи теории упругости.
Граничные условия имеют вид:
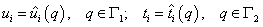 , ,
| (19.1а) |
где
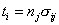 - компоненты вектора напряжений на границе;
- компоненты вектора напряжений на границе;
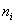 - компоненты вектора нормали к поверхности;
- компоненты вектора нормали к поверхности;
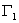 - часть границы, на которой заданы кинематические условия;
- часть границы, на которой заданы кинематические условия;
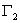 - часть границы, на которой заданы силовые условия.
- часть границы, на которой заданы силовые условия.
Вывод интегрального уравнения задачи
Вывод интегрального уравнения основан на преобразовании дифференциальных уравнений теории упругости в интегральные уравнения. Это может быть осуществлено с помощью теоремы Бетти о взаимности работ. Рассматриваются два состояния упругой среды:
1: 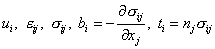
2: 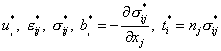 .
.
Оба состояния должны удовлетворять уравнению равновесия в 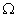 под действием заданных объемных сил, поверхностных нагрузок и перемещений.
под действием заданных объемных сил, поверхностных нагрузок и перемещений.
Пусть 1-е состояние определяется исходной постановкой задачи. В качестве второго возьмем следующее состояние упругой среды: область 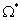 с границей
с границей 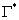 , которая включает в себя рассматриваемое тело
, которая включает в себя рассматриваемое тело 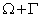 (рис. 19.2). Считается, что и эта область находится в состоянии равновесия, обозначенном символом «*». Пусть теперь в качестве вектора объемных сил b*k выступают единичные сосредоточенные усилия, приложенные в точке p (x1, x2, x3) в каждом из трех ортогональных направлений ek, т.е.
(рис. 19.2). Считается, что и эта область находится в состоянии равновесия, обозначенном символом «*». Пусть теперь в качестве вектора объемных сил b*k выступают единичные сосредоточенные усилия, приложенные в точке p (x1, x2, x3) в каждом из трех ортогональных направлений ek, т.е.
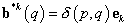
или
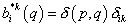 ,
,
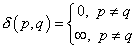 ,
,
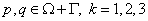 ,
,
где 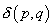 - дельта-функция Дирака.
- дельта-функция Дирака.
Возникающие поля перемещений и напряжений можно вычислить как решение полной системы уравнений теории упругости или эквивалентного ей уравнения Навье в области 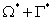 :
:
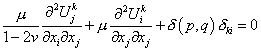 , ,
| (19.2) |
где 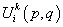 - i-я компонента вектора перемещений в точке q, от действия в точке p единичной сосредоточенной силы в направлении ek.
- i-я компонента вектора перемещений в точке q, от действия в точке p единичной сосредоточенной силы в направлении ek.
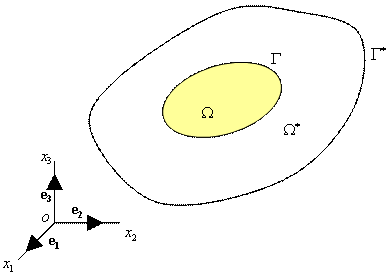
Рис. 19.2. Область 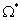 с границей
с границей 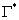 , которая включает в себя рассматриваемое тело
, которая включает в себя рассматриваемое тело 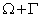 .
.
Решения этого уравнения называются фундаментальными сингулярными решениями. Они образуют тензоры фундаментальных решений U и Tс компонентами: 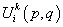
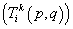 - i-я компонента вектора перемещений (напряжений) в точке q, вызванная действием единичной сосредоточенной силы в точке p в направлении ek.
- i-я компонента вектора перемещений (напряжений) в точке q, вызванная действием единичной сосредоточенной силы в точке p в направлении ek.
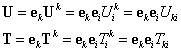 .
.
Тогда перемещения и напряжения в любой точке q тела при действии сосредоточенной единичной силы в точке p в направлении lопределяется так:
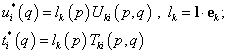 .
.
Теперь отсекаем область 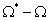 , и действие отброшенной части заменяем распределенными поверхностными нагрузками и перемещениями на границе
, и действие отброшенной части заменяем распределенными поверхностными нагрузками и перемещениями на границе 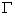 :
:
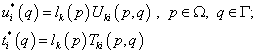 .
.
Оставшаяся часть области 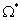 находится в равновесии и описывается следующими параметрами:
находится в равновесии и описывается следующими параметрами:
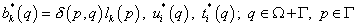 .
.
Теперь для области 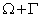 можно записать теорему Бетти:
можно записать теорему Бетти:
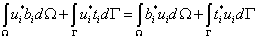 .
.
Подставляя 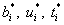 в уравнение взаимности работ, получаем:
в уравнение взаимности работ, получаем:
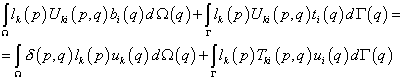 .
.
Используя фильтрующее свойство 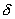 -функции
-функции
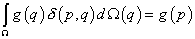 ,
,
получим интегральное уравнение задачи:
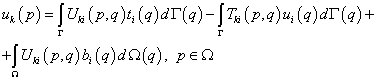 . .
| (19.3) |
Это выражение называется также тождеством Сомильяны для перемещений. Перейдем от тензорной формы записи к матричной:
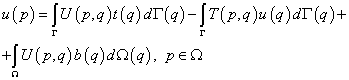 , ,
| (19.3а) |
где u, t, b – векторы столбцы; U, T – матрицы. Их размерность: dim u = dim t = dim b =3x1, dim U = dim T = 3x3.
Граничное интегральное уравнение
Согласно концепции метода граничных элементов рассматривается предельная форма интегрального уравнения (19.3а) при перемещении точки p к границе. Тогда (19.3а) приобретает вид:
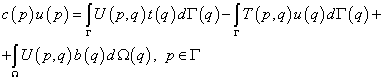 , ,
| (19.4) |
где c(p) – матрица, зависящая от гладкости границы Г в окрестности точки p.
Уравнение (19.4) справедливо как для трех-, так и для двухмерных задач, и представляет собой соотношение, которое должно выполняться между перемещениями и напряжениями на поверхности тела, а также объемными силами. Поскольку объемные силы известны, видно, что это граничное интегральное уравнение (ГИУ) относительно неизвестных граничных значений перемещений и усилий.
Контрольные вопросы
1. Сформулировать теорему Бетти о взаимности работ.
2. Что такое фундаментальные решения?
3. Записать граничное интегральное уравнение задачи теории упругости.
Лекция 20
Численная реализация метода граничных элементов
Гранично-элементная дискретизация
Решить ГИУ аналитически для произвольной области не представляется возможным. Поэтому применяется гранично-элементная дискретизация, аналогичная процедура МКЭ. Граница Г представляется серией граничных элементов (ГЭ) Ге, на каждом из которых перемещения и поверхностные усилия получаются интерполированием по узловым точкам элемента. Интегральный член с объемными силами опустим, т.к. для сути МГЭ он не имеет принципиального значения.
Дискретизованная модель границы области (Рис. 20.1) характеризуется глобальными векторами координат узлов X:
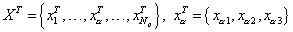 ,
,
где 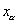 - вектор координат узла
- вектор координат узла  . Вектор координат узлов ГЭ
. Вектор координат узлов ГЭ 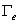 получается из глобального вектора координат при помощи матрицы кинематической связи:
получается из глобального вектора координат при помощи матрицы кинематической связи:
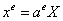 .
.
Координаты любой внутренней точки ГЭ 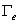 определяются с помощью матрицы интерполирующих функций
определяются с помощью матрицы интерполирующих функций
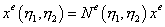 , ,
| (20.1) |
где 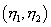 - локальная система координат ГЭ:
- локальная система координат ГЭ: 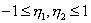 .
.
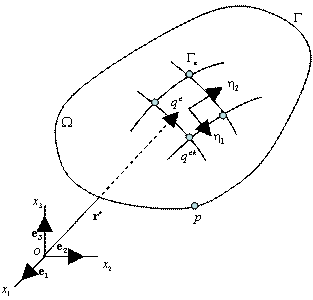
Рис. 20.1. Дискретизованная модель границы области (поверхности тела).
Аналогично в случае изопараметрического элемента определяются перемещения и поверхностные усилия через векторы узловых перемещений и усилий на ГЭ 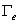 :
:
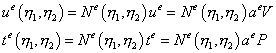 , ,
| (20.2) |
где V, P – глобальные векторы перемещений и усилий.
После разбиения границы на элементы ГИУ (19.4, лекция 19) принимает вид:
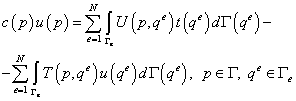 . .
| (20.3) |
В это выражение входят поверхностные интегралы по ГЭ 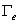 .
.
Элемент поверхности может быть записан так:
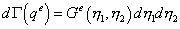 ,
,
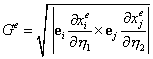 ,
,
где 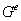 - якобиан преобразования от глобальной к локальной системе координат.
- якобиан преобразования от глобальной к локальной системе координат.
Подставляя в дискретизованное ГИУ выражение для 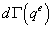 и интерполяционные соотношения для перемещений и усилий, получим:
и интерполяционные соотношения для перемещений и усилий, получим:
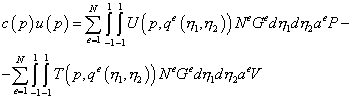 . .
| (20.4) |
Формирование системы линейных алгебраических уравнений
В уравнении (20.4) точка p расположена на границе произвольно. Согласно методу коллокаций выберем ее совпадающей последовательно с каждым из узлов границы. В результате получаем систему матричных уравнений ( 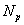 - глобальное число узлов границы):
- глобальное число узлов границы):
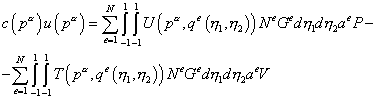 , ,
| (20.5) |
где 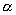 - глобальный номер узла.
- глобальный номер узла. 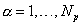 .
.
Последнее уравнение можно переписать в матричном виде:
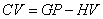 , ,
| (20.6) |
где
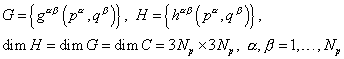 ,
,
где 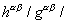 - матричный блок размерностью 3x3, который представляет собой сумму интегральных вкладов с ядрами
- матричный блок размерностью 3x3, который представляет собой сумму интегральных вкладов с ядрами 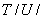 от всех ГЭ, содержащих узел с номером
от всех ГЭ, содержащих узел с номером  , а точка коллокации совпадает с узлом
, а точка коллокации совпадает с узлом 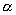 , т.е. этот матричный блок характеризует влияние узла
, т.е. этот матричный блок характеризует влияние узла  на узел с номером
на узел с номером 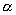 .
.
В уравнение (20.6) входят как известные из граничных условий перемещения и усилия, так и неизвестные, поэтому удобно разделить векторы V и P на известную часть и неизвестную:
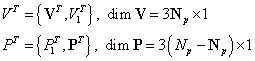 .
.
То есть в 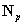 узлах заданы перемещения, а в
узлах заданы перемещения, а в 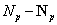 - усилия.
- усилия.
Соответствующим образом разделяются и компоненты матриц G и С+Н. Перенеся вектор известных величин в правую часть, получим окончательный вид системы линейных алгебраических уравнений метода граничных элементов:
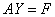 , ,
| (20.7) |
где 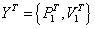 - вектор неизвестных поверхностных усилий и перемещений,
- вектор неизвестных поверхностных усилий и перемещений, 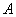 - полностью заполненная матрица размерности
- полностью заполненная матрица размерности 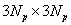 .
.
Как только все узловые граничные значения перемещений и усилий становятся известными в результате решения СЛАУ, то могут быть вычислены перемещения и напряжения внутри тела с помощью соответствующих дискретизованных уравнений. Напряжения в граничных узлах определяются по значениям перемещений и усилий на границе с использованием дифференцирования в пределах ГЭ.
Особенности математической формулировки МГЭ для решения плоских задач теории упругости
Граничное интегральное уравнение (19.4), выведенное в лекции 19 для пространственного случая, полностью сохраняет свой вид и для плоской задачи. Однако при гранично-элементной дискретизации следует учитывать, что область 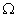 - есть двумерное плоское упругое тело, а граница
- есть двумерное плоское упругое тело, а граница 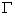 - есть контур этого тела (рис. 20.2). В многих разрабатываемых программах для моделирования кривой линии и распределения перемещения и усилий вдоль нее используются так называемые линейные элементы, функции формы которых имеют вид (рис. 20.3):
- есть контур этого тела (рис. 20.2). В многих разрабатываемых программах для моделирования кривой линии и распределения перемещения и усилий вдоль нее используются так называемые линейные элементы, функции формы которых имеют вид (рис. 20.3):
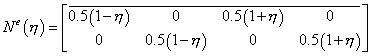 , ,
| (20.8) |
а вектор координат узлов ГЭ 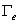 (рис. 20.2)
(рис. 20.2)
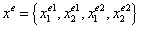 .
.

Рис. 20.2. Гранично-элементная дискретизация границы плоской области.
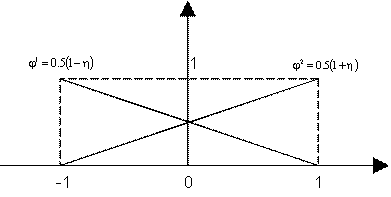
Рис. 20.3. Функции формы одномерного линейного изопараметрического элемента.
В силу этого интегрирование по граничному элементу будет означать интегрирование по отрезку 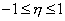 , а окончательная СЛАУ приобретает размерность
, а окончательная СЛАУ приобретает размерность 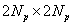 .
.
Здесь же приведем вид фундаментальных решений для плоской бесконечной области:
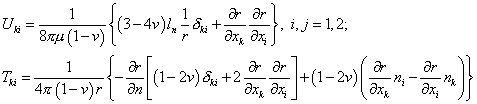 , ,
| (20.9) |
где r – расстояние между точкой коллокации 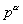 и произвольной точкой на ГЭ,
и произвольной точкой на ГЭ, 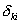 - символы Кронекера.
- символы Кронекера.
Как видно из рисунка 20.2, расстояние 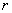 есть модуль вектора, соединяющего точки
есть модуль вектора, соединяющего точки 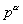 и
и 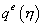 :
:
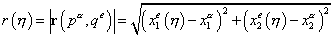 ,
,
тогда можно вычислить производные расстояния 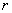 по координате
по координате 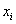 следующим образом:
следующим образом:
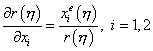 .
.
В выражении 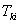 фигурирует производная расстояния
фигурирует производная расстояния 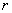 по нормали к границе
по нормали к границе 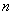 . Она вычисляется согласно правилу определения производной скалярной функции по направлению:
. Она вычисляется согласно правилу определения производной скалярной функции по направлению:
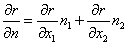 .
.
Приведенное фундаментальное решение (20.9) носит название решение Кельвина - Сомильяны. Оно получается как решение уравнения Навье (19.2, лекция 19) в случае, когда 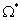 представляет собой бесконечную область, в произвольной точке
представляет собой бесконечную область, в произвольной точке 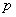 которой действует единичная сосредоточенная сила в направлении координатной оси
которой действует единичная сосредоточенная сила в направлении координатной оси 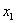 или
или 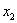 . Важнейшая особенность такого решения заключается в том, что перемещения и усилия, определяемые формулами (20.9), неограниченно возрастают при приближении точки
. Важнейшая особенность такого решения заключается в том, что перемещения и усилия, определяемые формулами (20.9), неограниченно возрастают при приближении точки 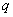 , в которой они вычисляются, к точке
, в которой они вычисляются, к точке 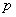 , в которой приложена сосредоточенная сила, т.е.
, в которой приложена сосредоточенная сила, т.е.
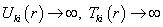
при
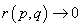 .
.
Поэтому решения такого вида называются сингулярными решениями, а точка 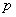 - сингулярной точкой
- сингулярной точкой 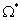 .
.
Контрольные вопросы
1. Дать понятие гранично-элементной дискретизации.
2. Записать и пояснить СЛАУ МГЭ.
3. Назвать свойства фундаментальных решений плоской задачи теории упругости.
Лекция 21
Программная реализация метода граничных элементов для решения плоских задач теории упругости
Общая схема алгоритма МГЭ
Первый этап – ввод исходных данных.
Данный этап, который является первым шагом выполнения любой инженерной программы, основан на концепции макроэлементов, позволяющей значительно сократить и упростить процедуру ввода чисел. Применительно к плоской задаче теории упругости она состоит в том, что вся граница исследуемой упругой области разбивается на простые линии, выбираемые из библиотеки макроэлементов. Такими линиями могут быть отрезок прямой, часть параболы, дуга окружности или целая окружность. Это так называемые графические примитивы, с помощью которых достаточно легко смоделировать границу любого плоского тела с высокой точностью.
Следовательно, минимальная вводимая информация должна содержать количество и тип макроэлементов, число разбиений каждого макроэлемента на граничные элементы, тип граничных условий, координаты узлов макроэлементов и значения граничных перемещений и усилий в узлах макроэлементов.
Второй этап – дискретизация границы области и аппроксимация граничных условий.
Для наиболее точного описания неизвестных заранее полей перемещений и напряжений введенные макроэлементы разбиваются на ряд граничных элементов 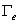 с помощью подпрограммы, носящей название «автоматический генератор данных». В результате разбиения формируются глобальные векторы узлов границы
с помощью подпрограммы, носящей название «автоматический генератор данных». В результате разбиения формируются глобальные векторы узлов границы 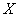 , узловых значений граничных перемещений
, узловых значений граничных перемещений 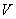 и усилий
и усилий 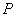 .
.
Координаты любой внутренней точки 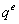 линейного элемента
линейного элемента 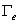 , представленного в виде отрезка прямой линии, определяются в соответствии с общими соотношениями (20.1, лекция 20) и конкретным видом функций формы (20.8, лекция 20):
, представленного в виде отрезка прямой линии, определяются в соответствии с общими соотношениями (20.1, лекция 20) и конкретным видом функций формы (20.8, лекция 20):
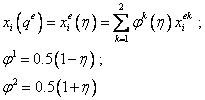 . .
| (21.1) |
Аналогично, интерполяционные формулы (20.2) определят значения перемещений и усилий в любой внутренней точке 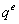 граничного элемента
граничного элемента 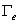 :
:
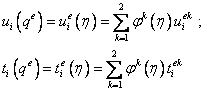 . .
| (21.2) |
Таким образом, глобальные векторы 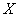 ,
, 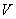 ,
, 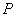 будут состоять из узловых значений
будут состоять из узловых значений 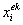 ,
, 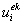 ,
, 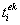 , где i=1,2; k=1,2; e=1,…,N.
, где i=1,2; k=1,2; e=1,…,N.
Третий этап – построение матриц влияния и формирования СЛАУ.
Рассмотрим дискретизованное ГИУ (20.4, лекция 20). В случае двумерной области дифференциал границы 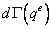 представляет собой бесконечно малый отрезок, длина которого
представляет собой бесконечно малый отрезок, длина которого
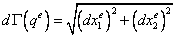 .
.
Используя соотношения (21.3), вычислим
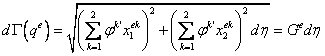 .
.
Величина 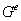 представляет собой якобиан преобразования от глобальной системы координат к локальной координате
представляет собой якобиан преобразования от глобальной системы координат к локальной координате 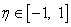 . Его легко вычислить в случае линейных функций форм. В самом деле,
. Его легко вычислить в случае линейных функций форм. В самом деле,
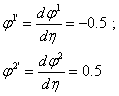 .
.
Следовательно,
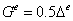 ,
,
где 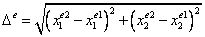 - длина граничного элемента
- длина граничного элемента 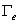 (рис. 20.2, лекция 20).
(рис. 20.2, лекция 20).
Таким образом, интегралы по граничному элементу 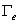 в глобальной системе координат
в глобальной системе координат 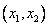 в выражении (20.3, лекция 20) преобразуются к интегралам по локальной координате
в выражении (20.3, лекция 20) преобразуются к интегралам по локальной координате 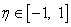 и ГИУ (20.3, лекция 20) после подстановки в него интерполяционных соотношений (21.2) примет вид:
и ГИУ (20.3, лекция 20) после подстановки в него интерполяционных соотношений (21.2) примет вид:
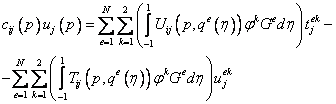 . .
| (21.3) |
Согласно методу коллокаций совместим последовательно точку 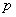 со всеми узлами границы:
со всеми узлами границы:

При этом глобальный размер узла 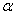 однозначно определяется номером граничного элемента
однозначно определяется номером граничного элемента 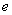 и локальным номером
и локальным номером 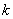 узла на элементе. Тогда ГИУ (21.3) примет вид системы
узла на элементе. Тогда ГИУ (21.3) примет вид системы 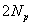 уравнений:
уравнений:
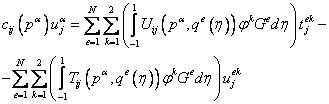 . .
| (21.4) |
Эта система алгебраических уравнений относительно переменных 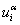 ,
, 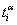 представляет собой развернутую запись матричного уравнения (20.7, лекция 20) для двумерной области
представляет собой развернутую запись матричного уравнения (20.7, лекция 20) для двумерной области 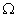 .
.
Из соотношений (21.4) видно, что глобальные матрицы влияния 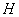 и
и 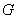 состоят из элементарных интегральных выражений, образующих матричные блоки
состоят из элементарных интегральных выражений, образующих матричные блоки 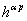 ,
, 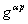 , где глобальный номер узла
, где глобальный номер узла 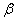 определяется через номер элемента и локальный номер узла
определяется через номер элемента и локальный номер узла 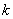 -
- 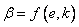 :
:
Дата добавления: 2015-06-17; просмотров: 1050;
