Естественные координаты элемента 1 страница

Согласно общей концепции построения произвольного изопараметрического конечного элемента, введем в рассмотрение естественную локальную систему координат на элементе, соответствующую геометрии данного типа элемента. Естественной системой координат трехстороннего элемента являются треугольные координаты 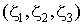. Естественной системой координат плоского четырехстороннего элемента является система координат 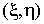, показанная на рис. 10.1 для двух вариантов четырехстороннего элемента, имеющего прямолинейные либо криволинейные стороны. Данная система координат относится к известному широкому классу недекартовых координат – криволинейных косоугольных, в общем случае, координат. Несмотря на очевидные отличия от декартовой системы, криволинейные косоугольные координат обладают сходными математическими свойствами.

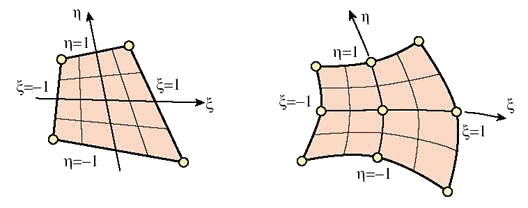
Рис. 10.1. Четырехсторонние двумерные элементы в криволинейных косоугольных координатах.

Локальная система координат 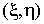является масштабированной. Это означает, что каждая координата изменяется в пределах от -1 на одной стороне элемента до +1 на противоположной стороне, принимая нулевое значение на медианах. Заметим, что пределы изменения локальных координат могут быть выбраны произвольно, например, от 0 до 1. Преимущество введенных пределов состоит в том, что они обеспечивают эффективное применение формул интегрирования Гаусса, что будет обсуждаться в следующих лекциях.

При разработке алгоритмов МКЭ часто бывает удобно визуализировать произвольный конечный элемент в декартовых координатах на плоскости 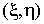(Рис. 10.2). Любой четырехсторонний конечный элемент в этом случае может быть представлен квадратом со стороной 2 в безразмерных единицах в пределах 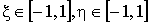. Взаимооднозначное преобразование между локальной системой координат 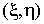и глобальной описывается математическими уравнениями общего вида:

,

(10.1)

В случае произвольного двумерного конечного элемента первая часть формул (10.1) могут быть представлена следующим образом:

,

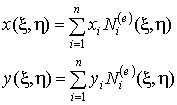(10.2)

где n – число узлов на элементе.

Соотношения типа (10.1) или (10.2) носят название изопараметрического отображения. Вопрос корректности отображения может быть достаточно острым при расчетах методом конечных элементов. Необходимо правильное построение сетки конечных элементов, чтобы не было нарушения взаимооднозначности отображения (Рис. 10.2).

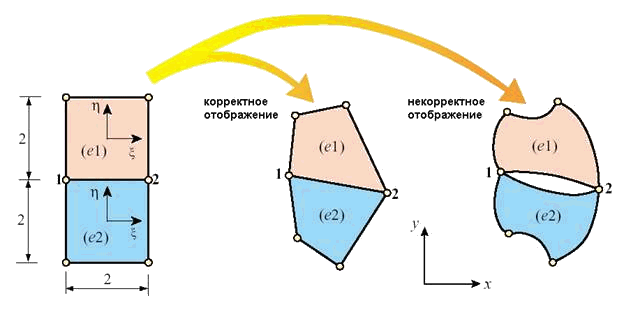
Рис. 10.2. Отображение элемента, заданного в естественных локальных координатах 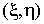, на тот же элемент в глобальной системе координат .

В случае корректного отображения имеет место взаимооднозначное соответствие точек элемента в плоскостях 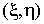и . В случае некорректного отображения взаимооднозначное соответствие нарушается. Так например, видно, что любой одной точке на линии 1-2 в плоскости 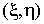соответствует две точки в плоскости .

Четырехсторонний билинейный элемент

Четырех-узловой четырехсторонний конечный элемент является простейшим представителем семейства четырехсторонних двумерных элементов. Его вид показан на рис. 10.3, а базовые интерполяционные соотношения представлены следующим образом:

(10.3)

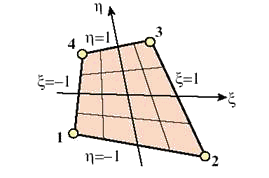
Рис. 10.3. Четырех-узловой четырехсторонний билинейный элемент.

Функции формы элемента выражены следующими соотношениями через локальные естественные координаты:

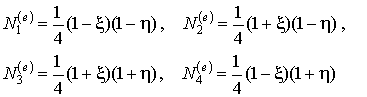
(10.4)

Отметим, что функции формы (10.4) изменяются линейно вдоль координатных линий и 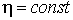. Однако, они не являются линейными полиномами как в случае треугольного линейного элемента. Такие функции и соответственно элементы, ими описываемые, носят название билинейных. На рис. 10.4 приведен графический вид одной из функций формы.

Рис. 10.4. Четырехсторонний билинейный элемент: (а) геометрия элемента; (б) уравнения сторон, противоположных первому узлу; (в) вид функции формы .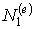

Четырехсторонние элементы высшего порядка

Рассмотрим следующие два варианты семейства четырехсторонних элементов: девяти-узловой и восьми-узловой изопараметрический конечный элемент, показанные на рис. 10.5. Очевидное внешнее отличие между этими элементами состоит в наличии или отсутствии внутреннего узла в центре элемента.

Интерполирующие соотношения элемента первого типа, носящего название биквадратичный изопараметрический элемент, имеют вид:

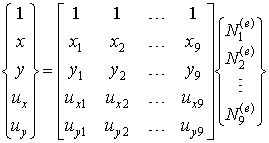
(10.5)

Рис. 10.5. Четырехсторонние конечные элементы высшего порядка: (а) девяти-узловой биквадратичный элемент; (б) восьми-узловой «серендипов» элемент.

Приведем формулы для некоторых характерных функций формы биквадратичного конечного элемента (Рис. 10.6):

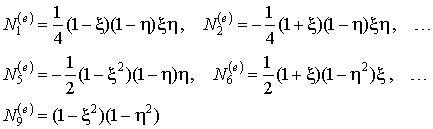
(10.6)

Интерполирующие соотношения элемента второго типа, носящего название изопараметрический элемент серендипова семейства, имеют вид:

,

(10.7)

где функции формы могут быть представлены следующим образом:

,

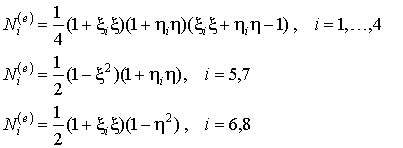(10.8)

где 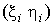- локальные координаты i-го узла на элементе.

Рис. 10.6. Графики характерных функций формы биквадратичного конечного элемента.

Заметим, что соотношения (10.4) линейного элемента также могут быть представлены в компактной форме, удобной для программирования:

(10.9)

Обратим внимание, что функции формы (10.8) изменяются по квадратичному закону вдоль координатных линий и 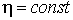. Функция формы, связанная с внутренним девятым узлом элемента, в англоязычной литературе по МКЭ называется bubble function, что связано с характерной «пузырчатой» формой этой функции. В случае элемента серендипова семейства внутренний узел исключается из рассмотрения путем наложения специальных кинематических связей:

(10.10)

Функции формы серендипова конечного элемента строятся таким образом, чтобы их сумма равнялась нулю, и порядок аппроксимации был равен двум по обеим локальным координатам. Отсюда получают два условия для определения констант 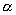и .

Свойство полноты

Отметим коротко очень важное условие для обеспечения сходимости метода конечных элементов, которому должен подчиняться выбор или построение интерполирующих функций (или, что то же самое, функций формы) – свойство полноты. Множество функций формы называется полным, если эти функции могут точно описать (аппроксимировать) любую линейную функцию перемещений, заданную в виде:

,

(10.11)

где 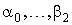- произвольные константы.

Проверим, удовлетворяют ли рассмотренные функции формы и соответствующие приближенные решения (9.4, лекция 9) данному условию. Вычислим перемещения в узлах согласно соотношениям (10.11):

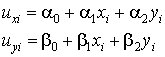
(10.12)

Подставим 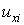в первое интерполяционное соотношение (9.4, лекция 9). Получим:

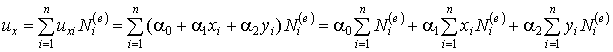
Подставим геометрические интерполяционные соотношения изопараметрического элемента (9.3, лекция 9) в последнее выражение. Получим первое из соотношений (10.11). Аналогичные вычисления могут быть выполнены для компоненты 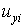. Таким образом, изопараметрические функции формы удовлетворяют свойству полноты.

Контрольные вопросы

1. Дать понятие естественных координат четырехстороннего конечного элемента.

2. Записать базовые интерполирующие соотношения билинейного и квадратичного изопараметрического четырехстороннего конечного элемента.

3. Дать понятие полноты аппроксимирующей функции.

Лекция 11

Вычисление матрицы градиентовизопараметрического элемента

Введение

В настоящей и следующей лекции будет подробно рассмотрен алгоритм формирования матриц жесткости конечных элементов (6.23, лекция 6):

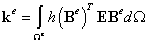
(11.1)

В лекции 8 мы уже вычисляли матрицу жесткости линейного треугольного элемента. Однако, рассмотренный путь вычислений справедлив только для единственного двумерного элемента - линейного треугольного элемента. Для треугольных элементов высших порядков и для четырехсторонних элементов, широко используемых в конечно-элементных программах, данный подход не применим по причине его неуниверсальности. Дело в том, что линейный треугольный элемент – это единственный двумерный элемент, матрицы жесткости которого могут быть вычислены в явном и замкнутом виде. В остальных случаях, и тем более для трехмерных задач, необходима разработка универсальных алгоритмов, пригодных для программирования.

В общем случае алгоритм формирования ключевой характеристики механического элемента – его матрицы жесткости – включает следующие шаги:

1. Построение функций формы элемента;

2. Вычисление частных производных от функций формы элемента для формирования матрицы градиентов, связывающей деформации и перемещения на элементе;

3. Численное интегрирование по площади (или объему в трехмерном случае) для окончательного вычисления матрицы жесткости.

Ниже будут рассмотрены основные шаги представленного алгоритма на примере изопараметрического четырехстороннего конечного элемента как наиболее характерного представителя семейства универсальных двумерных элементов. При этом будем полагать, что функции формы элемента уже построены (см. лекцию 10). Таким образом, основное внимание будет сосредоточено на вычислении частных производных от функций формы и численном интегрировании, а также некоторых других важных моментах эффективного вычисления компонент матриц жесткости.

Матрица градиентов

Знание выражений частных производных от функций формы элемента по глобальным координатам необходимо для вычисления матрицы градиентов В, входящей в выражения деформаций (5.7б, лекция 5) и напряжений (5.11, лекция 5) в произвольной точке элемента. Однако, как было показано в предыдущих лекциях, функции формы явно зависят только от локальных координат , связанных с элементом. Зависимость же от глобальных координат задается сложной функцией многих переменных.

Итак, рассмотрим произвольный четырехсторонний изопараметрический конечный элемент, заданный n узлами. Матрица градиентов имеет вид (5.8, лекция 5):

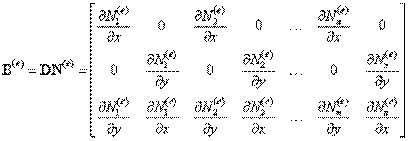
(11.2)

Введем следующие обозначения для сокращения записи. Пусть матрица градиентов представлена в виде матричной строки, образованной блоками (3x2):

,

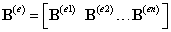(11.3)

где произвольный блок, связанный с узлом i имеет вид:

,

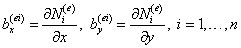
(11.4)

Таким образом, необходимо вычислить 2n компонент матрицы градиентов . Дело облегчается тем, что расчетные формулы можно получить в достаточно общем виде. Покажем это.

Матрицы Якоби

Пусть функции формы представлены сложной функцией многих переменных:

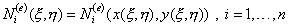
(11.5)

Пользуясь правилом вычисления частных производных сложной функции, можем записать:

(11.6)

Соотношения (11.6) представляют собой систему двух уравнений относительно неизвестных частных производных , поскольку производные функций формы по локальным координатам могут быть легко вычислены, т.к. функции формы заданы в локальных координатах. Запишем для удобства (11.6) в матричных обозначения:

,

(11.7)

где J – матрица Якоби (называемая также якобианом преобразования), состоящая из частных производных и определяющая однозначное отображение элемента, заданного в глобальных координатах , на «единичный» элемент в локальной плоскости :

Рассмотрим вычисление матрицы Якоби:

(11.8)

Элементы матрицы представляют собой частные производные от глобальных координат точек элемента по соответствующим локальным координатам. Эти производные могут быть легко вычислены для изопараметрического элемента по геометрическим интерполирующим соотношениям (10.2, лекция 10):

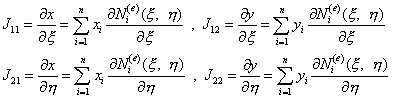
(11.9)

После того как определены компоненты матрицы Якоби, система (11.7) может быть разрешена относительно неизвестных функций :

,

(11.10)

где 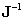представляет собой обратную матрицу Якоби.

Согласно правилам вычисления обратных матриц можно записать следующее выражение для :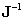

(11.11)

где - определитель матрицы Якоби, также иногда называемый якобианом:

(11.12)

Окончательно, можно записать выражения 2n искомых компонент матрицы градиентов в развернутом виде:

,

(11.13)

где - общее количество элементов в конечно-элементной сетке, называемое глобальным числом конечных элементов.

Обратим внимание на особенности формул (11.13):

1. В общем случае все входящие в формулы переменные являются функциями локальных естественных координат элемента , включая компоненты матрицы Якоби и якобиан, что следует из правил их вычисления (11.9);

2. Компоненты матрицы Якоби и якобиан зависят только от номера элемента (геометрии элемента), но не связаны с номером узла на элементе. В то же время, функции формы естественным образом связаны с номером узла на элементе, что приводит к однозначной зависимости компонент матрицы градиентов от локального номера узла на элементе.

3. Формулы удобны для программирования и применимы для многих разновидностей конечных элементов, в частности, с некоторой модификацией рассмотренный подход легко распространяется и на более сложные трехмерные конечные элементы.

Таким образом, определены выражения 2n искомых компонент матрицы градиентов и, следовательно, могут быть сформированы матрицы градиентов любого элемента согласно формулам (11.3).

Замечание

Заметим, что обратная матрица Якоби определяет обратное отображение «единичного» элемента в локальной плоскости на элемент, определенный в глобальных координатах :

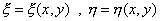
По определению якобиана преобразования, можно записать:

,

(11.14)

где – матрица Якоби обратного преобразования.

Покажем, что совпадает с 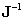. Для этого достаточно перемножить две матрицы:

,

(11.15)

Получение в результате единичной матрицы и доказывает наше предположение о том, что матрица совпадает с .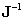

Строгие условия, наложенные на форму элементов, гарантируют взаимооднозначное отображение между элементами в локальной и глобальной плоскостях, что показано ниже.

Ограничения на геометрию элементов

Для того чтобы имело место взаимооднозначное соответствие между координатами точек элемента в глобальной и локальной системах координат:

и

,

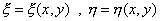необходимо, чтобы якобиан преобразования (11.12), т.е. определитель матрицы Якоби, был строго положителен.

В литературе, посвященной математическим аспектам метода конечных элементов доказывается, что это условие выполняется, если узловые углы, образованные сторонами элемента, лежат в пределах от нуля до 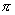(Рис. 10.1).

Рис. 10.1. Четырехсторонний конечный элемент с требуемыми узловыми углами.

Таким образом, необходимо строго следить за выполнением этого условия и не допускать появления в конечно-элементной сетке элементов, показанных например на рис. 10.2. В отмеченных случаях, либо вообще алгоритм формирования не сможет быть выполнен из-за деления на ноль, либо решение, несмотря ни на что, будет получено, но его достоверность не сможет быть обоснована. Заметим, что второй случай несравненно более опасный, чем первый. Вы сможете получить ответ и будете думать, что решили задачу. Однако, расчетное решение по построенной модели может оказаться очень далеким от реальной физической ситуации. Очень опасно, если такое инженерное решение окажется внедренным и воплощенным в некоторой технической конструкции или механизме.

Рис. 10.2. Примеры четырехсторонних конечных элементов с некорректными значениями узловых углов.

Контрольные вопросы

1. Дать понятие матрицы Якоби и якобиана.

2. Вычислить матрицу градиентов изопараметрического четырехстороннего конечного элемента.

3. Перечислить ограничения на геометрию изопараметрического четырехстороннего конечного элемента.

Лекция 12

Формирование матрицы жесткости изопараметрического элемента

Введение

В настоящей лекции будет подробно рассмотрен алгоритм формирования матрицы жесткости конечных элементов (6.23, лекция 6):

,

(12.1)

где - матрица градиентов элемента е;

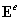- матрица упругих модулей элемента е;

- толщина элемента е;

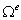- площадь элемента е.

Вычисление матриц жесткости представляет собой одну из наиболее сложных процедур в алгоритме метода конечных элементов. Проблема формирования включает в себя две задачи:

1. Структура матрицы. Несмотря на то, что мы уже знаем ее общий вид (12.1), структура матрицы остается пока terra incognita, и кроме того, значительно, хотя и не принципиально, зависит от типа элемента.

2. Численное интегрирование по области или объему (для трехмерных элементов).

Рассмотрим первую из задач.

Структура матрицы жесткости

Очевидно, что структура матрицы жесткости определяется подынтегральным выражением формулы (12.1). Очевидно также, что толщина элемента не влияет на структуру матрицы. Поэтому достаточно рассмотреть произведение трех подынтегральных матриц, чтобы представить себе общий вид матрицы жесткости.

Обозначим:

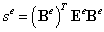
(12.2)

Тогда:

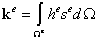
(12.3)

Раскроем выражение (12.2), перемножив матрицы градиентов и упругих модулей, пользуясь блочным представлением (11.3, лекция 11):

,

(12.4)

Из выражения (12.4) видно, что искомая матрица имеет блочную структуру, определяемую числом узлов элемента n. При этом каждый блок зависит от номеров двух локальных узлов элемента и может быть записан следующим образом:

,

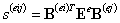(12.5)

Соответственно, и матрица жесткости имеет аналогичную матричную структуру, состоящую из блоков:

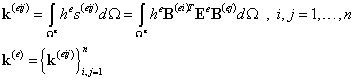
(12.6)

В принципе, для разработки алгоритма и программной реализации вычисления матрицы жесткости приведенных формул уже достаточно. Современные языки программирования позволяют производить матричные перемножения с помощью встроенных процедур и функций. Для моделей, содержащих небольшое число элементов, это приемлемо. Однако, число операций, требуемых для перемножения матриц, будет критическим в случае большого количества элементов. Поэтому в коммерческих программах принято проводить эту операцию вручную с тем, чтобы уменьшить конечное число машинных операций перемножения. Кроме того, выполнение этой процедуры вручную полезно с точки зрения понимания полной структуры матрицы жесткости. Поэтому раскроем выражение (12.5), еще раз перемножив матрицы.

Матрица упругих модулей

Пусть двумерное тело находится в плоско-напряженном или плоско-деформированном состоянии (см. лекцию 4). Тогда определяющие соотношения имеют вид:

Плоско-напряженное состояние

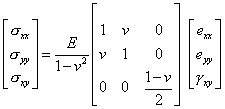
(12.7а)

Плоско-деформированное состояние

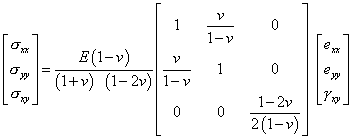
(12.7б)

Запишем оба выражения (12.7а и б) в едином виде для повышения универсальности алгоритма:

,

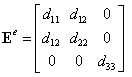(12.8)

где определяются соотношениями (12.7а) и (12.7б).

Заметим также, что выражение (12.8) подходит также для записи матрицы упругих модулей ортотропного материала.

Выражение компонент матрицы жесткости элемента

Раскроем формулу (12.5), перемножив матрицы:

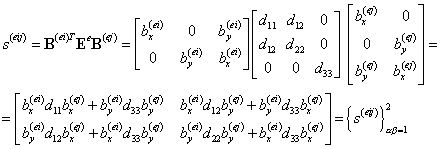
(12.9)

Таким образом, видно, что элементарный блок матрицы жесткости двумерного изопараметрического элемента 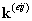(12.6) есть матрица размером 2x2. Поскольку таких блоков в элементной матрице жесткости nxn, то окончательный размер матрицы жесткости есть 2n x2n.