Естественные координаты элемента 3 страница
2. Матрица жесткости симметрична:
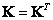
| (14.16) |
3. Хотя мы специально не доказывали свойство (14.16), его легко проверить на примере (14.12), если учесть, что элементные матрицы жесткости симметричны, т.е.:

| (14.17) |
4. Матрица жесткости является положительно-определенной, что означает, что квадратичная форма:
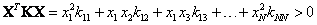
| (14.18) |
5. при любых 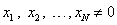 .
.
6. Свойства положительной определенности и симметрии матрицы являются необходимыми для построения или применения известных более эффективных алгоритмов решения СЛАУ, чем метод исключения Гаусса.
7. Матрица является ленточной и редко-заполненной, что означает, что ненулевые элементы матрицы сосредоточены вблизи главной диагонали. Следовательно, для эффективного использования машинной памяти и расчета достаточно хранить только ненулевые элементы ленты матрицы. Размер ленты, т.е. число ненулевых элементов в ней, существенно зависит от конкретного вида конструкции и способа нумерации узлов. В среднем можно принять, что размер ленты равен приблизительно числу уравнений, входящих в систему.
8. Большие матрицы могут быть плохо-обусловленными. Число обусловленности равно отношению максимального собственного числа матрицы к минимальному и существенно влияет на устойчивость и точность численного решения. Число обусловленности сильно зависит размеров и формы конечных элементов. Поэтому необходимо внимательно следить за построением сетки и избегать больших градиентов размеров элементов, а также слишком больших или слишком малых углов между сторонами элементов.
Метод треугольной факторизации Холецкого
Метод треугольной факторизации Холецкого является одним из самых популярных прямых методов решения СЛАУ МКЭ, поскольку он учитывает все положительные свойства матрицы жесткости, отмеченные выше. К сожалению, он применим, как и все прямые методы, к относительно небольшим системам уравнений (до 104 уравнений). Связано это с внутренней машинной проблемой: при любой реальной точности хранения чисел и операций умножения и деления, достижимой на данном компьютере, ошибка вычислений, тем не менее, накапливается и при большом числе операций может стать катастрофической. Единственным выходом в данной ситуации является применение итеративных методов решения СЛАУ, свободных от данной проблемы.
Итак, рассмотрим вкратце алгоритм Холецкого. Подробное описание и расчетные формулы есть во всех книгах по вычислительной математике.
1. Треугольное разложение матрицы K. Представим матрицу K в виде произведения трех матриц:
 , ,
| (14.19) |
2. где  - нижняя треугольная матрица с единицами на главной диагонали;
- нижняя треугольная матрица с единицами на главной диагонали;
3.  - диагональная матрица, причем все
- диагональная матрица, причем все 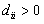 .
.
4. Прямой ход. Решаем систему линейных алгоритмических уравнений в три этапа. Обозначим  и решим СЛАУ:
и решим СЛАУ:
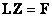
| (14.20) |
5. В результате найдем вектор 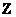 .
.
6. Масштабирование. Решаем СЛАУ с диагональной матрицей, обозначив 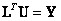 :
:

| (14.21) |
7. Обратная подстановка. Последний шаг – вычисляем искомый вектор перемещений путем решения СЛАУ с нижней диагональной матрицей:
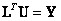
| (14.22) |
Вычисление напряжений
После решения СЛАУ определены все узловые перемещения. Теперь с помощью интерполирующих соотношений можно определить деформации и напряжения в любой точке конечного элемента по формулам (5.7, 5.10, лекция 5):
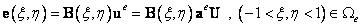
| (14.23) |
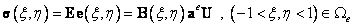
| (14.24) |
Заметим, что точки  могут быть любыми на элементе. Однако, для повышения эффективности и точности вычислений, обычно деформации и напряжения определяются в точках квадратур Гаусса, а затем экстраполируются в узлы элемента.
могут быть любыми на элементе. Однако, для повышения эффективности и точности вычислений, обычно деформации и напряжения определяются в точках квадратур Гаусса, а затем экстраполируются в узлы элемента.
Лекция 15
Алгоритм МКЭ для трехмерной задачи теории упругости. Часть 1.
Введение
Динамическая задача линейной теории вязко-упругости (Рис. 15.1) описывается хорошо известной системой тензорных уравнений в заданном объеме сплошной среды V с граничными условиями кинематического или силового типа на ее поверхности S = S1 + S2:
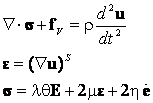 , ,
| (15.1) |
где 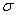 ,
, 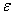 - тензора напряжений и деформаций;
- тензора напряжений и деформаций;
e - девиатор тензора деформаций: 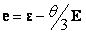 ;
;
E - единичный тензор;
u=u(r,t) - вектор перемещений, зависящий от времени t и радиуса вектора точек сплошной среды r;
fv=fv(r,t)- вектор заданных объемных сил, зависящий от времени t и радиуса вектора точек сплошной среды r;
 ,
,  ,
,  - коэффициенты Ламе и вязкость материала;
- коэффициенты Ламе и вязкость материала;
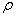 - плотность;
- плотность;
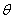 - объемная деформация;
- объемная деформация;
 - дифференциальный оператор Гамильтона.
- дифференциальный оператор Гамильтона.
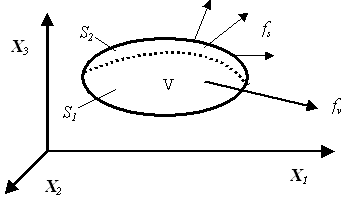
Рис. 15.1. Постановка общей задачи теории упругости.
Коэффициенты Ламе, используемые в записи обобщенного закона Гука, связаны с техническими константами материала: модулем упругости Е, модулем сдвига G и коэффициентом Пуассона 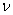 следующими соотношениями:
следующими соотношениями:

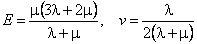
Приведенная дифференциальная постановка задачи теории упругости эквивалентна вариационной постановке в виде принципа минимума потенциальной энергии Лагранжа или принципа возможных перемещений:
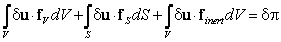
| (15.2) |
где  - вектор возможных перемещений точек сплошной среды;
- вектор возможных перемещений точек сплошной среды;
 - вектор сил инерции;
- вектор сил инерции;
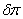 - вариация потенциальной энергии деформации тела:
- вариация потенциальной энергии деформации тела:
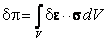
| (15.3) |
Интегралы слева представляют собой работы внешних объемных и поверхностных сил, а также сил инерции на возможных перемещениях.
Алгоритм
1. Первым шагом общего алгоритма МКЭ является разбиение упругой области на ряд непересекающихся подобластей простой формы, называемых конечными элементами (Рис. 15.2). Во многих конечно-элементных программах этот шаг носит название генерации конечно-элементной сетки.

Рис. 15.2. Разбиение тела на конечные элементы.
Согласно процедуре конечно-элементной дискретизации области, формируются элементные вектора, содержащие в определенной последовательности координаты узлов соответствующего конечного элемента:

и глобальный вектор координат узлов, содержащий координаты всех узлов сетки:
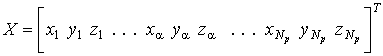
Каждый элементный вектор связан с глобальным вектором с помощью алгебраического матричного соотношения:
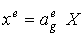 ,
,
где 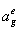 представляет собой матрицу связи, состоящую из нулей и единиц.
представляет собой матрицу связи, состоящую из нулей и единиц.
Наконец, координаты любой внутренней точки p элемента могут быть определены с помощью интерполяционного соотношения через заданные координаты узлов конечного элемента:
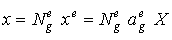 ,
,
где 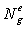 - матрица интерполирующих функций или, согласно другой терминологии, функций формы. Вид матрицы и образующих ее функций существенно зависит от типа используемого конечного элемента.
- матрица интерполирующих функций или, согласно другой терминологии, функций формы. Вид матрицы и образующих ее функций существенно зависит от типа используемого конечного элемента.
2. Вторым важным этапом общего алгоритма МКЭ является аппроксимация искомых функций – функции перемещений при использовании вариационного принципа Лагранжа. В случае так называемых изопараметрических конечных элементов формулы, записанные выше, легко преобразуются для описания неизвестных перемещений.
В частности, имеем:
элементный вектор перемещений:
 ,
,
где u 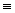 ux
ux
v 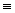 uy
uy
w 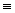 uz
uz
глобальный вектор перемещений:
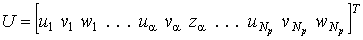 ,
,
соотношение между элементными и глобальным векторами:
 ,
,
перемещение в любой внутренней точке p конечного элемента:
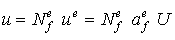 ,
,
где
 ,
,
Отметим, что в случае изопараметрического конечного элемента имеют место простые соотношения:
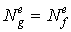
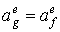
3. Основным и наиболее трудоемким этапом в методе конечных элементов является формирование системы алгебраических уравнений, следующих из соответствующего вариационного принципа, в рассматриваемом случае - из принципа минимума потенциальной энергии Лагранжа или эквивалентного ему принципа возможных перемещений. В качестве альтернативного подхода к выводу глобальной системы алгебраических конечно-элементных уравнений может быть предложен известный из теории приближенных решений математический метод взвешенных невязок. Обладая несомненной универсальностью, метод взвешенных невязок, тем не менее, требует дополнительных знаний из общей теории приближенных методов, а также требует большего числа математических операций при выводе алгоритма. Поэтому в настоящем изложении основ МКЭ мы воспользуемся более очевидным для инженера-механика принципом возможных перемещений.
Согласно общему подходу конечно-элементной дискретизации, преобразуем алгебраические и дифференциальные соотношения, связывающие непрерывные векторные и тензорные переменные, к матричной форме между узловыми векторами.
3.1. Кинематическое соотношение.
Тензорное соотношение, линейно связывающее кинематические переменные упругого движения: тензор деформаций и вектор перемещений (второе уравнение в системе 15.1), преобразуется к матричному виду следующим образом:
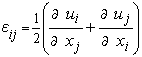
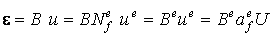 ,
,
где
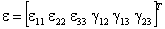 есть матричный вектор, образованный шестью независимыми компонентами тензора деформаций,
есть матричный вектор, образованный шестью независимыми компонентами тензора деформаций,
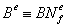 - так называемая матрица градиентов, состоящая из частных производных от интерполирующих функций,
- так называемая матрица градиентов, состоящая из частных производных от интерполирующих функций,
B - символическая матрица, образованная частными производными по пространственным координатам:
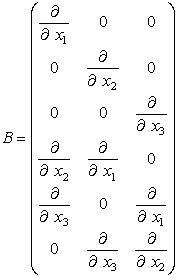
3.2. Определяющее соотношение, задающее связь деформаций и напряжений в точке сплошной среды (третье уравнение в системе 15.1).
В качестве определяющего соотношения идеальной упругости рассмотрим обобщенный закон Гука, задающий линейную связь напряжений с деформациями. В матричной форме закон Гука принимает следующий вид:
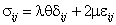
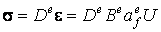 ,
,
где 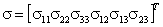 есть матричный вектор, образованный шестью независимыми компонентами тензора напряжений,
есть матричный вектор, образованный шестью независимыми компонентами тензора напряжений,
D - матрица упругих модулей:

В случае кусочно-однородной сплошной среды различным элементам соответствуют материалы с различными упругими постоянными, и следовательно, матрица D будет существенным образом зависеть от номера элемента. В общем случае непрерывного изменения упругих постоянных, характерного для описания как твердых, так и мягких тканей, может быть предложен приближенный подход, сводящий непрерывно-неоднородную область к большому числу конечных элементов, описываемых осредненными в пределах элемента матрицами упругости. Однако, возможен и другой вариант, при котором упругие модули считаются функциями координат, что приводит к необходимости вычисления более сложных интегралов по объему конечного элемента как будет ясно из дальнейшего.
Отметим, что в данном случае мы рассмотрели только вариант изотропной сплошной среды. Матрица упругих модулей в общем случае анизотропной среды выводится аналогичным образом из обобщенного закона Гука, включающего в себя большее число независимых упругих констант.
Контрольные вопросы
1. Постановка динамической задачи линейной теории упругости.
2. Записать принцип возможных перемещений.
3. Записать матрицу упругих модулей.
Лекция 16
Алгоритм МКЭ для трехмерной задачи теории упругости. Часть 2.
Введение
Данная лекция является продолжением предыдущей. В ней будет закончен разбор общего алгоритма МКЭ применительно к трехмерной задачи теории упругости. Затем будет получено динамическое уравнение метода конечных элементов и рассмотрен алгоритм расчета вязко-упругих колебаний конструкций.
Алгоритм (продолжение)
3.3. Формирование глобальной системы алгебраических уравнений.
Формирование глобальной системы алгебраических уравнений осуществляется путем преобразования исходного вариационного соотношения. В данном случае мы используем уравнение принципа возможных перемещений (15.2, лекция 15).
Проведем предварительные преобразования и вычислим:
Вариация вектора перемещений:
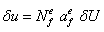
Вариация вектора деформаций:
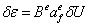
Вариация потенциальной энергии деформации тела (15.3, лекция 15):
 ,
,
где
 - элементная матрица жесткости
- элементная матрица жесткости
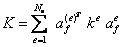 - глобальная матрица жесткости
- глобальная матрица жесткости
Элементарная работа внешних объемных и поверхностных сил на возможных перемещениях:
 ,
, 
где
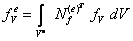 - элементный вектор объемных узловых сил
- элементный вектор объемных узловых сил
 - элементный вектор поверхностных узловых сил
- элементный вектор поверхностных узловых сил
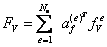 - глобальный вектор объемных узловых сил
- глобальный вектор объемных узловых сил
 - глобальный вектор поверхностных узловых сил
- глобальный вектор поверхностных узловых сил
Заметим, что записанные выше элементные и глобальные вектора узловых сил статически эквивалентны объемным и поверхностным силам, заданным на данном элементе или во всем объеме тела.
Наконец, используя основную формулировку принципа возможных перемещений (15.2, лекция 15), согласно которой виртуальная работа внешних сил равна вариации потенциальной энергии деформации тела:
 , ,
| (16.1) |
и подставляя затем в данное равенство полученные выше выражения элементарной работы и вариации энергии деформации, сравнивая выражения слева и справа, получим следующее матричное уравнение:
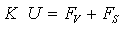
| (16.2) |
Данное выражение является основным разрешающим соотношением метода конечных элементов и представляет собой систему линейных алгебраических уравнений относительно узловых перемещений. После корректного наложения заданных кинематических граничных условий уравнение может быть решено одним из известных численных методов, применяемых в теории решения больших систем с разреженными матрицами.
4. После определения глобального вектора узловых перемещений:

могут быть вычислены деформации и напряжения в любой точке каждого элемента по записанным выше формулам, а, следовательно, будут получены значения деформаций и напряжений в произвольных точках тела:

Алгоритм МКЭ для динамической задачи
При анализе динамического поведения биологических структур, требуемого в ряде задач биомеханики, как правило, необходимо учитывать вязкость живых тканей. В теории наследственной упругости и в работах, посвященных моделированию мягких тканей, известно большое число определяющих соотношений вязко-упругого материала, задающих связь между скоростями деформаций и напряжений. В настоящем курсе мы рассмотрим наиболее известную модель такого материала, носящую название модель Кельвина-Фойгта и описываемую следующим тензорным соотношением (15.1, лекция 15):

Приведенное выражение позволяет достаточно легко расширить рассмотренный выше алгоритм на решение динамических задач с учетом вязкости материала. В частности, модель Кельвина-Фойгта удобна для анализа отклика биомеханической системы на приложенное гармоническое воздействие. В одной из следующих лекциях будет продемонстрирован пример применения данной модели к решению некоторых актуальных задач биомеханики опорно-двигательного аппарата человека.
Перепишем определяющее соотношение модели Кельвина-Фойгта в матричной форме, введя в рассмотрение наряду с матрицей упругих модулей D еще и матрицу вязкости S:
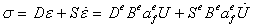
С учетом нового выражения для вектора напряжений вычислим вариацию потенциальной энергии деформации тела:
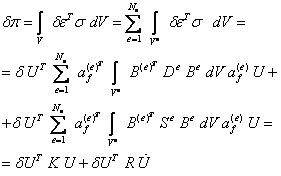
где
 - элементная матрица диссипации
- элементная матрица диссипации
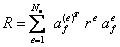 - глобальная матрица диссипации
- глобальная матрица диссипации
Вектор сил инерции может быть выражен через глобальный вектор узловых ускорений путем применения процедуры конечно-элементной дискретизации, описанной выше:
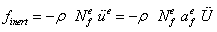
Элементарная работа внешних объемных сил должна быть преобразована с учетом сил инерции, действующих на точки тела. Согласно принципу Даламбера силы инерции могут быть добавлены к активным внешним силам, что в результате приводит к следующему выражению виртуальной работы объемных сил:

где
 - элементная матрица масс
- элементная матрица масс
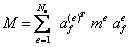 - глобальная матрица масс
- глобальная матрица масс
Наконец, применяя основное математическое выражение принципа возможных перемещений (15.4, лекция 15):
 ,
,
с учетом нового вида виртуальной работы и вариации потенциальной энергии деформации, получим следующее обыкновенное дифференциальное уравнение относительно глобального вектора узловых перемещений в матричном виде:
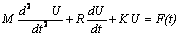 , ,
| (16.3) |
где U(t) - глобальный вектор узловых перемещений, зависящих от времени,
F(t)= Fv(t)+Fs(t) - глобальный вектор узловых сил, зависящих от времени.
Полученное дифференциальное уравнение широко используется в методе конечных элементов для решения динамических задач. В данной главе мы рассмотрим только частный случай общей динамической задачи - вынужденные колебания тела под действием внешней гармонической силы. Несмотря на частный характер, теоретический анализ вынужденных колебаний биомеханических структур актуален при решении важных практических задач, связанных с разработкой вибрационных методов исследования состояния живых тканей и органов, что будет показано в дальнейшем.
Расчет вязко-упругих гармонических колебаний
Для разработки алгоритма воспользуемся известным подходом, применяемым в теории линейных колебаний. Представим внешнюю гармоническую силу в виде комплексной экспоненты:
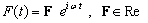 ,
,
где F, 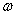 - глобальный вектор амплитудных значений узловых сил и круговая частота колебаний силы, i - мнимая единица.
- глобальный вектор амплитудных значений узловых сил и круговая частота колебаний силы, i - мнимая единица.
Тогда частное решение, соответствующее установившемся вынужденным колебаниям ищется в том же виде, что и правая часть дифференциального уравнения:
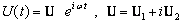 ,
,
где U - глобальный вектор комплексных амплитудных значений узловых перемещений; U1 and U2 - соответственно действительная и мнимая части данного вектора.
Подставляя выражения сил и перемещений в дифференциальное уравнение, получим систему комплексных алгебраических уравнений относительно глобального вектора комплексных амплитуд:
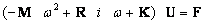
| (16.4) |
После решения полученной системы для фиксированных значений частоты внешней силы, действительные амплитудные значения перемещений узлов, их скоростей и ускорений могут быть вычислены следующим образом:
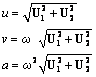
Представленный алгоритм реализован в авторском конечно-элементном комплексе MechanicsFE и позволяет рассчитывать установившиеся колебания упругих тел с учетом вязкости материала, что принципиально отличает разработанный программный код от известного коммерческого конечно-элементного комплекса ANSYS, в котором закон диссипации представлен в виде закона Релея:
 ,
,
где 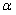 и
и  - константы.
- константы.
Совместное использование представленных пакетов при решении ряда актуальных задач биомеханики нижней конечности человека позволило с большей достоверностью определить резонансные частоты биологических структур голени и уточнить значения вязкости тканей согласно модели Кельвина-Фойгта.
Контрольные вопросы
1. Записать выражения вариации потенциальной энергии деформации тела и элементарной работы внешних сил.
2. Записать основное динамическое уравнение МКЭ.
3. Объяснить алгоритм расчета вязко-упругих гармонических колебаний.
Лекция 17
Современные программные средства конечно-элементного анализа
Программные системы
Развитие метода конечных элементов обусловлено взаимосвязью трех факторов: наличием высокопроизводительной вычислительной техники; разработкой математических моделей исследуемых явлений, адекватных реальным процессам с достаточной степенью точности; особенностями самого метода [26].
Первые программные комплексы, в которых реализован метод конечных элементов, были разработаны в 60-х годах. К ним относятся STRUDL-II, SAP-IV, NONSAP, ASKA, NASTRAN, SESAM-69 и другие [41]. Появлению этих универсальных программных систем в силу особенностей метода конечных элементов предшествовало создание высокопроизводительных электронно-вычислительных машин, таких, например, как IBM-370. Начиная с конца 70-х годов в СССР появилось несколько десятков программных комплексов для разных ЭВМ, в которых был реализован МКЭ. К их числу относятся МИРАЖ [13], МОРЕ [27], КАСКАД-2 [28], ПРОЧНОСТЬ-75 [17], МКЭ/20 [10], МАРС [11], ПАРСЕК [7], ЛИРА [14], СПРИНТ [34], FEA [4] и ряд других программ [33].
В США и ряде других стран дальнейшее развитие МКЭ и необходимость в проведении расчетов конструкций на прочность также способствовали дальнейшему развитию уже созданных программных комплексов и разработке новых. Были разработаны сотни программных комплексов, предназначенных для приближенного решения самых разнообразных задач не только из области механики деформируемого твердого тела, но и из таких областей как гидродинамика, акустика, электротехника и т.д. Наибольшее распространение из них получили [40]: ABAQUS, ADINA, ASKA/DYNAN, ANSYS [2], MARC, MSC/NASTRAN [35], EUFEMI, COSMOS, HERCULE, MODULEF, SAP-7, LS-DYNA.
Отметим, что разработка программных комплексов является дорогостоящим делом. Поэтому, как правило, организации и фирмы – собственники разработанных программ, рассматривают их как коммерческий научно-технический продукт. Регулярно печатаемые обзоры существующих комплексов программ и их характеристик, сведения о программах в отраслевых фондах алгоритмов и программ позволяют пользователям программной продукции целенаправленно выбирать необходимые для их деятельности программы расчета.
Дата добавления: 2015-06-17; просмотров: 1082;
