Определение деформаций и напряжений. 3 страница
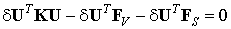
| (6.32) |
Отсюда получаем:
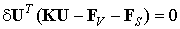
| (6.33) |
Поскольку вариация глобального вектора узловых перемещений представляет собой вектор, состоящий из независимых произвольных вариаций узловых перемещений, то в общем случае он отличен от нуля. Следовательно, в ноль должно обращаться выражение в круглых скобках. Откуда получаем разрешающую систему конечно-элементных уравнений относительно глобального вектора узловых перемещений:
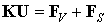
| (6.34) |
Матричное уравнение (6.34) представляет собой стандартную форму записи системы линейных алгебраических уравнений метода конечных элементов (СЛАУ МКЭ). Особенности формирования входящих в нее матриц и векторов и особенности решения СЛАУ будут рассмотрены в следующих лекциях.
Контрольные вопросы
1. Сформулировать принцип минимума потенциальной энергии.
2. Вычислить вариацию потенциальной энергии деформации тела.
3. Вычислить элементарную работу внешних сил.
Лекция 7
Треугольный линейный конечный элемент: система координат и интерполяция.
Введение
В данной лекции будут рассмотрены особенности формирования системы линейных алгебраических уравнений метода конечных элементов (СЛАУ МКЭ) на примере трехузлового треугольного элемента с линейной интерполяцией перемещений, применяемого для решения плоской задачи теории упругости. Для краткости будем называть такой элемент линейным треугольным конечным элементом.
Этот элемент имеет ряд отличительных особенностей:
1. Он принадлежит к семейству так называемых изопараметрических элементов, о чем будет говориться в следующих лекциях;
2. Он позволяет получить выражения элементных матриц жесткости и элементных векторов сил в замкнутой форме, что означает отсутствие необходимости в численном интегрировании при вычислении элементных матриц жесткости и элементных векторов сил;
3. Точность решения, обеспечиваемая данным элементом, не может быть повышена путем добавления внутренних степеней свободы.
В дополнение хотелось бы отметить, что линейный треугольный конечный элемент имеет определенное историческое значение. Он был одним из двух первых конечных элементов, представленных в статье Мартина, Тернера, Клоха и Топпа в 1956 году. Эта публикация общепризнанно считается началом современного метода конечных элементов.
Хотя линейный треугольный конечный элемент в настоящее время реже используется при расчетах конструкции ввиду его низкой точности, тем не менее, он широко используется в тех случаях, когда нет необходимости в высокоточных расчетах, например, концентрации напряжений в конструкции. Другая причина широкого применения треугольного элемента состоит в том, что он очень удобен при использовании в алгоритмах автоматической генерации сетки, например, в широко известном и популярном алгоритме триангулизации по Делоне.
Параметрическое представление функций
В дальнейшем изложении существенным образом будет использоваться понятие параметрического представления функции. Совместно с алгоритмами численного интегрирования данный подход играет ключевую роль в системной разработке различных типов конечных элементов для решения двумерных и трехмерных задач механики деформируемых тел.
Основная идея параметрического представления функции может быть продемонстрирована на простейшем примере. Рассмотрим каноническое уравнение окружности единичного радиуса с центром в начале координат:
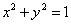
| (7.1) |
Кроме канонического представления (7.1) уравнение окружности может быть представлено в виде стандартной функциональной зависимости:
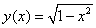 , ,
| (7.2) |
а также в полярной системе координат:
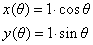
| (7.3) |
В представлении (7.3) 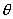 есть полярный угол, который может быть интерпретирован в виде независимого скалярного параметра, меняющегося в заданных пределах. Очевидно, что подстановка (7.3) в (7.1) дает тождественное равенство.
есть полярный угол, который может быть интерпретирован в виде независимого скалярного параметра, меняющегося в заданных пределах. Очевидно, что подстановка (7.3) в (7.1) дает тождественное равенство.
В общем случае параметрическое представление кривой линии на плоскости или в пространстве имеет вид:
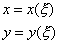 , ,
| (7.4а) | |
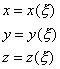 , ,
| (7.4б) | |
где 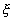 - независимый скалярный параметр, меняющейся в заданных пределах.
- независимый скалярный параметр, меняющейся в заданных пределах.
Вид функций, входящих в (7.4), может быть любым. Главное условие, наложенное на эти функции, состоит в том, чтобы каждому значению параметра 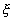 однозначно соответствовала бы точка на плоскости, имеющая координаты
однозначно соответствовала бы точка на плоскости, имеющая координаты 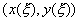 , или в пространстве -
, или в пространстве - 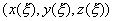 .
.
Аналогично определяется параметрическое представление куска плоскости на координатной плоскости или куска поверхности в трехмерном пространстве:
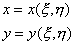 , ,
| (7.5а) | |
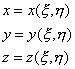 , ,
| (7.5б) | |
Здесь 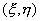 - система двух независимых параметров, меняющихся в заданных пределах. Вид функций, входящих в (7.5), может быть также любым. Главное условие, наложенное на эти функции, состоит в том, чтобы имело место взаимооднозначное соответствие системы параметров
- система двух независимых параметров, меняющихся в заданных пределах. Вид функций, входящих в (7.5), может быть также любым. Главное условие, наложенное на эти функции, состоит в том, чтобы имело место взаимооднозначное соответствие системы параметров 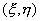 и координат
и координат  в соотношении (7.5а). В случае соотношения (7.5б) достаточно выполнения одного соответствия точки на плоскости
в соотношении (7.5а). В случае соотношения (7.5б) достаточно выполнения одного соответствия точки на плоскости 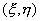 и точки на поверхности в пространстве
и точки на поверхности в пространстве 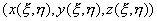 .
.
Параметрическое представление функций существенным образом используется в алгоритмах метода конечных элементов.
Система координат треугольного элемента
Геометрия трехузлового треугольного конечного элемента задается тремя угловыми точками в плоскости  - узлами конечного элемента (Рис. 7.1). Локальные номера узлов на элементе: 1, 2, 3; причем узлы нумеруются таким образом, чтобы обход по контуру элемента был бы против часовой стрелки, если смотреть со стороны внешней нормали к плоскости пластины. Напомним, что внешняя нормаль к плоскости пластины совпадает с положительным направлением глобальной оси z. Положение узлов определяется декартовыми координатами в глобальной системы координат:
- узлами конечного элемента (Рис. 7.1). Локальные номера узлов на элементе: 1, 2, 3; причем узлы нумеруются таким образом, чтобы обход по контуру элемента был бы против часовой стрелки, если смотреть со стороны внешней нормали к плоскости пластины. Напомним, что внешняя нормаль к плоскости пластины совпадает с положительным направлением глобальной оси z. Положение узлов определяется декартовыми координатами в глобальной системы координат:
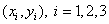
| (7.6а) |
Линейный треугольный конечный элемент имеет шесть степеней свободы, образуемые компонентами элементного вектора узловых перемещений:
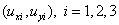
| (7.6б) |
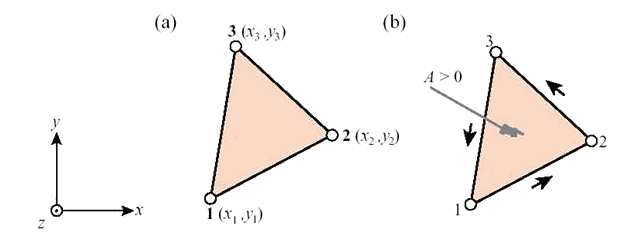
Рис. 7.1. Линейный треугольный конечный элемент: (а) – геометрия элемента; (б) – положительное направление обхода контура элемента.
Обозначим площадь элемента через А. Согласно известной формуле линейной алгебры, площадь плоского треугольника может быть вычислена с помощью определителя, составленного из координат вершин треугольника. Следовательно, площадь линейного треугольного конечного элемента равна:
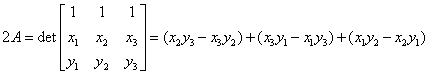
| (7.7) |
Заметим, что площадь области, определяемой формулой (7.7), имеет знак. Она положительна, если локальная нумерация узлов (1, 2, 3) выполнена против часовой стрелки, если смотреть со стороны внешней нормали к плоскости пластины, как это было отмечено выше и показано на рисунке 7.1. В противном случае, знак А будет отрицательным, что сигнализирует об ошибке. Такое соглашение будет использоваться и в дальнейшем изложении материала.
Кроме глобальной системы координат 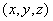 введем локальную параметрическую систему координат в плоскости элемента, задаваемую тремя переменными величинами:
введем локальную параметрическую систему координат в плоскости элемента, задаваемую тремя переменными величинами:
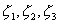
| (7.8) |
Эти три локальные параметрические координаты в литературе по МКЭ называются также естественными и треугольными. С помощью введенной системы координат устанавливается взаимооднозначное соответствие между глобальными декартовыми координатами произвольной точки элемента и тремя скалярными параметрами 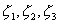 :
:
 , ,
| (7.9) |
Сразу обратим внимание на кажущееся противоречие между формулами (7.9) и (7.5а), которое легко устраняется, если допустить наличие связи между параметрами 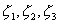 . На самом деле, так оно и есть: три треугольные координаты не являются независимыми, а связаны одним соотношением:
. На самом деле, так оно и есть: три треугольные координаты не являются независимыми, а связаны одним соотношением:
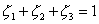
| (7.10) |
Очевидно, что из соотношения (7.10) можно выразить, например, координату 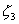 через другие две
через другие две 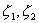 . Тогда соотношение (7.9) примет стандартный вид (7.5а). Однако, использование трех параметров оказывается более удобным с точки зрения вычислений и разработки эффективных численных алгоритмов, о чем всегда необходимо помнить, когда имеешь дело с вычислительной механикой.
. Тогда соотношение (7.9) примет стандартный вид (7.5а). Однако, использование трех параметров оказывается более удобным с точки зрения вычислений и разработки эффективных численных алгоритмов, о чем всегда необходимо помнить, когда имеешь дело с вычислительной механикой.
На рисунке 7.2 дано геометрическое пояснение математического смысла введенных координат.
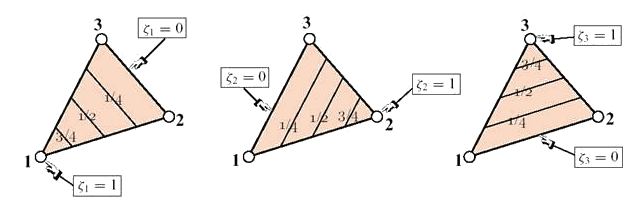
Рис. 7.2. Треугольные координаты.
Три уравнения, записанные в виде:

| (7.11) |
геометрически представляют собой множество прямых линий, параллельных стороне, противоположной i-му узлу.
Например, уравнения сторон треугольного элемента 1-2, 2-3 и 3-1 будут иметь следующий вид:
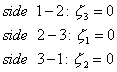
| (7.12а) |
Три вершины треугольного элемента будут иметь следующие локальные координаты:
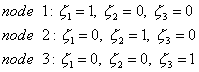
| (7.12б) |
В качестве примера приведем также координаты средних точек сторон треугольного элемента и геометрического центра элемента:
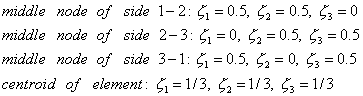
| (7.12в) |
Еще раз напомним, что три параметра не являются независимыми и связаны одним дополнительным соотношением:
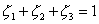
Интерполяционные соотношения линейного треугольного элемента
Рассмотрим произвольную непрерывную функцию двух переменных, которая изменяется линейно в пределах некоторой плоской треугольной области. В декартовой системе координат эта функция может быть записана следующим образом:
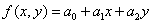 , ,
| (7.13) |
где 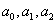 - произвольные постоянные коэффициенты.
- произвольные постоянные коэффициенты.
Пусть теперь мы хотим ввести аппроксимацию данной функции в пределах треугольного элемента. Обозначим через:
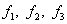 , ,
| (7.14) |
значения данной функции в соответствующих узлах конечного элемента – так называемые узловые значения функции.
С помощью этих значений могут быть определены неизвестные коэффициенты в представлении (7.13). В самом деле, получим:
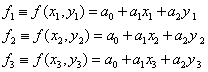 , ,
| (7.15) |
Соотношения (7.15) представляют систему трех линейных алгебраических уравнений относительно неизвестных коэффициентов 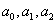 . Решив систему (7.15), получим однозначное выражение функции (7.13) через ее узловые значения. Однако, это выражение достаточно сложное и неудобное в использовании. Поэтому используют представление функции не в глобальной, а в локальной системе координат на элементе. Очевидно, что если установлено взаимооднозначное соответствие между глобальной и локальной системами координат, то и выражения функции в различных координатах будут соответственными друг другу.
. Решив систему (7.15), получим однозначное выражение функции (7.13) через ее узловые значения. Однако, это выражение достаточно сложное и неудобное в использовании. Поэтому используют представление функции не в глобальной, а в локальной системе координат на элементе. Очевидно, что если установлено взаимооднозначное соответствие между глобальной и локальной системами координат, то и выражения функции в различных координатах будут соответственными друг другу.
Используя данный подход, представим функцию (7.13) в треугольных координатах через ее узловые значения следующим образом:
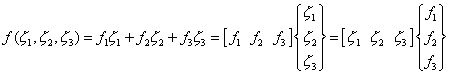
| (7.16) |
Соотношение (7.16) называется линейным интерполирующим соотношением произвольной непрерывной функции f в треугольных координатах.
В следующей лекции, пользуясь введенными понятиями, получим расчетные соотношения линейного треугольного конечного элемента.
Контрольные вопросы
1. Дать понятие параметрического представления функций.
2. Перечислить основные свойства треугольной системы координат.
3. Записать интерполяционные соотношения линейного треугольного элемента.
Лекция 8
Треугольный линейный конечный элемент: вывод расчетных соотношений
Преобразование координат
Математические величины, которые тесно связаны с геометрией треугольного конечного элемента, естественным образом выражаются через треугольные координаты 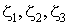 . С другой стороны, такие физические величины как перемещения, деформации и напряжения часто выражены в декартовых координатах
. С другой стороны, такие физические величины как перемещения, деформации и напряжения часто выражены в декартовых координатах  . Следовательно, необходимы уравнения, связывающие эти две системы координат, с помощью которых возможно переходить от одной системы координат к другой.
. Следовательно, необходимы уравнения, связывающие эти две системы координат, с помощью которых возможно переходить от одной системы координат к другой.
Используя универсальное соотношение (7.16, лекция 7), глобальные декартовые координаты произвольной точки на треугольном элементе  могут быть выражены через глобальные координаты узлов элемента и локальные треугольные координаты этой же точки
могут быть выражены через глобальные координаты узлов элемента и локальные треугольные координаты этой же точки 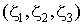 :
:
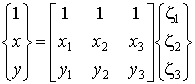 , ,
| (8.1) |
где 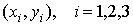 - глобальные декартовы координаты узлов треугольного элемента.
- глобальные декартовы координаты узлов треугольного элемента.
Поясним матричное выражение (8.1). Мысленно развернем его. Тогда первое уравнение будет выражать собой тот факт, что сумма трех локальных координат равна единице. Два последних уравнения представят собой развернутые интерполяционные соотношения глобальных координат точек треугольного элемента (См. ур-е 7.16, лекция 7):
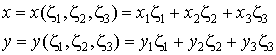
| (8.2) |
Разрешим систему (8.1) относительно вектора 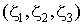 . Найдем обратную матрицу к матрице системы (8.1) и запишем решение в виде:
. Найдем обратную матрицу к матрице системы (8.1) и запишем решение в виде:
 , ,
| (8.3) |
где А – определитель матрицы системы (8.1), численного совпадающий с площадью треугольного элемента (7.7, лекция 7).
Введем обозначения:
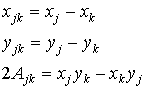 , ,
| (8.4) |
где 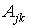 - математически представляет собой площадь треугольника, образованного двумя вершинами элемента и центром глобальной системы координат;
- математически представляет собой площадь треугольника, образованного двумя вершинами элемента и центром глобальной системы координат; 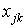 ,
, 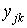 - проекции длин сторон элемента на оси глобальной системы координат. Очевидно, что если начало координат расположено в центре элемента, то
- проекции длин сторон элемента на оси глобальной системы координат. Очевидно, что если начало координат расположено в центре элемента, то 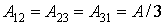 .
.
В обозначениях (8.4) решение (8.3) примет вид:
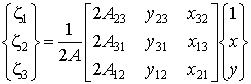
| (8.5) |
Вычисление частных производных
Из соотношений (8.2) и (8.5) легко вычисляются частные производные по соответствующим координатам:
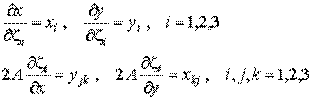
| (8.6) |
Во второй строке формул (8.6) последовательность 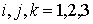 представляет собой круговую перестановку индексов. Например, если
представляет собой круговую перестановку индексов. Например, если 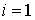 , то
, то 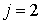 и
и 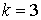 . Если
. Если 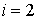 , то
, то 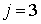 и
и 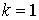 .
.
Рассмотрим произвольную непрерывную функцию двух переменных, которая изменяется линейно в пределах некоторой плоской треугольной области (См. формулы 7.13 и 7.16 лекции 7). Эта функция может быть представлена как в глобальной декартовой системе координат  , так и в локальной треугольной системе координат
, так и в локальной треугольной системе координат 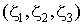 . Представим ее как сложную функцию многих переменных:
. Представим ее как сложную функцию многих переменных:
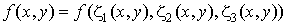
| (8.7) |
Вычислим теперь частные производные функции (8.7) по глобальным координатам, воспользовавшись правилом дифференцирования сложной функции многих переменных:
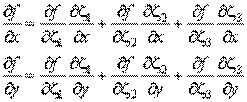
| (8.8) |
Подставим (8.6) в (8.8). Получим выражения частных производных произвольной непрерывной функции по глобальным координатам через три частные производные той же функции по локальным треугольным координатам:
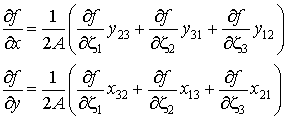
| (8.9) |
Окончательно в матричной форме система частных производных произвольной непрерывной функции по глобальным координатам примет вид:

| (8.10) |
Таким образом, мы получили все необходимые математические формулы для вывода уравнений, описывающих треугольный линейный конечный элемент.
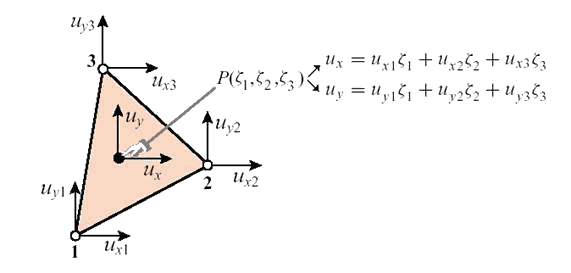
Рис. 8.1. Интерполяция перемещений в пределах треугольного линейного конечного элемента.
Вывод уравнений треугольного линейного конечного элемента
Интерполяция перемещений
В случае треугольного линейного конечного элемента предполагается, что перемещения в пределах элемента изменяются линейно по пространственным координатам. Это означает, что компоненты вектора перемещений в любой произвольной точке элемента 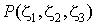 могут быть представлены с помощью интерполяционного соотношения 7.16 лекции 7, которое в данном случае примет вид:
могут быть представлены с помощью интерполяционного соотношения 7.16 лекции 7, которое в данном случае примет вид:
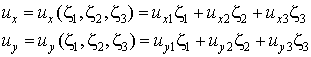
| (8.11) |
Здесь 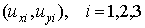 - компоненты вектора перемещений в узлах конечного элемента (Рис. 8.1).
- компоненты вектора перемещений в узлах конечного элемента (Рис. 8.1).
Интерполяционное соотношение для перемещений (8.11) может быть также представлено в стандартной для метода конечных элементов матричной форме (см. формулы 5.6, лекция 5):
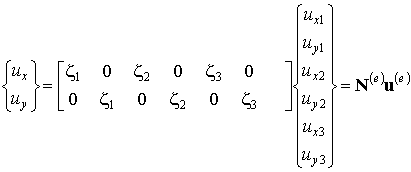 , ,
| (8.11а) |
где 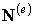 - матрица интерполирующих функций,
- матрица интерполирующих функций, 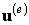 - элементный вектор узловых перемещений.
- элементный вектор узловых перемещений.
Очевидно, что в рассматриваемом случае треугольного линейного конечного элемента интерполирующие функции 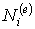 равны треугольным координатам:
равны треугольным координатам:
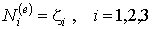
| (8.12) |
Кинематические уравнения
Компоненты тензора деформаций (вектор деформаций) вычисляются путем дифференцирования вектора перемещений, что приводит к общей формуле (5.7) лекции 5:
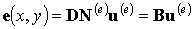
| (8.13) |
где 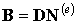 - матрица градиентов.
- матрица градиентов.
Вычислим матрицу градиентов. Согласно формуле (5.8) лекции 5:
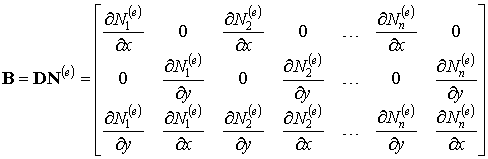
| (8.14) |
Интерполирующие функции могут быть интерпретированы как сложные функции многих переменных:
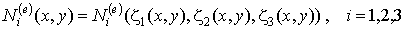
| (8.15) |
С другой стороны, в явном виде они совпадают с треугольными координатами элемента (см. формулу 8.12). Тогда применяя формулы вычисления частных производных функций подобного типа по глобальным координатам (8.9) и (8.6), получим выражение матрицы градиентов:
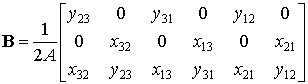
| (8.16) |
Обратим внимание, что деформации (8.13) получились постоянными на элементе, поскольку компоненты матрицы градиентов – проекции сторон элемента – постоянные величины.
Определяющие соотношения
Определяющее соотношение анизотропного идеально-упругого материала записывается в виде хорошо известного закона Гука. В матричном виде оно было получено в лекции 5. Здесь мы его еще раз приведем для полноты изложения:
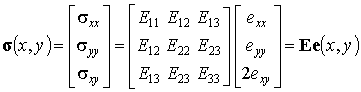 , ,
| (8.17) |
где 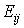 - упругие модули материала.
- упругие модули материала.
Если считать, что упругие свойства материал не меняются на элементе, то, поскольку деформации постоянны, напряжения также постоянны на элементе.
Элементные матрицы жесткости
Для задачи о плоско-деформированном состоянии тела общий вид матриц жесткости был получен в лекции 6. Напомним его:
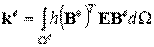
| (8.18) |
Как было отмечено выше, матрицы градиентов и упругих модулей постоянны для рассматриваемого треугольного линейного конечного элемента. Следовательно, их произведение может быть вынесено за знак интеграла:
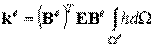
| (8.19) |
Если элемент имеет постоянную толщину (h=const), то h также выносится за знак интеграла по площади элемента, который, таким образом, легко вычисляется и будет равен площади элемента А. В результате, получим выражение элементной матрицы жесткости:
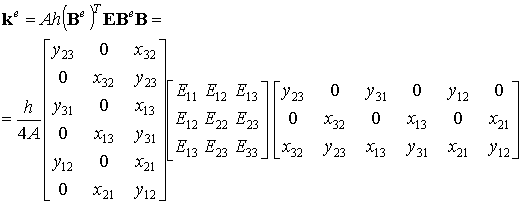
| (8.20) |
Заметим, что все геометрические переменные и модули упругости могут быть разными на разных элементах и, следовательно, зависят от номера элемента е.
Элементные вектора узловых сил
Для простоты рассмотрим сейчас только вычисление элементного вектора узловых сил, статически эквивалентных заданным объемным силам. Причем, пусть объемные силы представляют собой плотность сил собственного веса тела (сила на единицу объема):
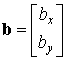
| (8.21) |
Согласно общей формуле вычисления вектора объемных узловых сил:
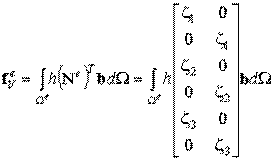
| (8.22) |
Пусть толщина элемента постоянна и плотность объемных сил также постоянна. Тогда h и b могут быть вынесены за знак интеграл и необходимо вычислить только интегралы от 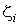 по площади элемента:
по площади элемента:
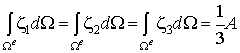
| (8.23) |
Здесь мы воспользовались известной математической формулой вычисления интеграла по площади треугольника:
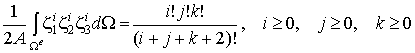
| (8.24) |
Таким образом, вычисляя интегралы от интерполирующих функций и перемножая полученную матрицу на вектор b, получим окончательное выражение элементного вектора узловых сил, статически эквивалентных заданным постоянным объемным силам:
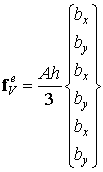
| (8.25) |
Заметим, что полученные компоненты вектора узловых сил совпадают с результатом простого равномерного распределения суммарной силы, равной Ahb, между тремя узлами.
Контрольные вопросы
1. Записать формулы вычисления частных производных функции на треугольном элементе.
2. Вычислить матрицу градиентов линейного треугольного элемента.
3. Вычислить элементную матрицу жесткости и элементного вектора узловых сил.
Лекция 9
Изопараметрический подход в МКЭ
Введение
Техника построения линейного треугольного конечного элемента, изложенная в предыдущих лекциях, формально может быть распространена на четырехсторонние или трехсторонние элементы высокого порядка. Однако, это немедленно приведет к ряду трудностей:
Дата добавления: 2015-06-17; просмотров: 1099;
