Определение деформаций и напряжений. 1 страница

После определения узловых перемещений в соответствии с известными соотношениями теории упругости могут быть определены деформации и напряжения.

Контрольные вопросы

1. Перечислить основные шаги численного моделирования.

2. Основное уравнение МКЭ.

3. Перечислить шаги общего алгоритма МКЭ.

Лекция 3

Понятие о конечных элементах

Определение

Как было отмечено в предыдущих лекциях, метод конечных элементов представляет собой наиболее распространенный приближенный метод в механике твердого тела и может быть интерпретирован с физической или математической точки зрения.

Основа физической концепции МКЭ – это разбиение математической модели конструкции на непересекающиеся компоненты (подобласти) простой геометрии, называемые конечными элементами или просто элементами для краткости. Множество элементов, на которые разбита конструкция, называется конечно-элементной сеткой. Механическое поведение каждого элемента выражается с помощью конечного числа степеней свободы или значений искомых функций во множестве узловых точек. Поведение математической модели, таким образом, аппроксимируется поведением дискретной модели, полученной путем сборки или ансамблирования всех элементов. Заметим, что концепция разбиения-сборки естественно возникает при исследовании многих искусственных или живых систем. Например, легко представить мост, здание, двигатель или скелет, как сложную систему, составленную из простых компонентов. Заметим также, что в отличие от метода конечных разностей, конечные элементы не накладываются друг на друга в пространстве.

Атрибуты элемента

Рассмотрим основные типы конечных элементов и их свойства, называемые атрибутами элементов (Рис. 3.1).

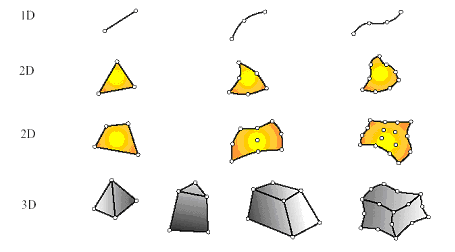
Рис. 3.1. Основные типы конечных элементов для одно-, дву- и трехмерных задач механики.

1. Собственная размерность.Конечные элементы могут описываться одной, двумя или тремя пространственными координатами в зависимости от размерности задачи, для решения которой они предназначены. Соответствующее число внутренних или локальных координат называется собственной размерностью элемента. В динамическом анализе время рассматривается как дополнительная размерность. Отметим, что в расчетах используются также специальные элементы с нулевой размерностью, такие как, точечные массы или сосредоточенные упругие элементы (пружины).

2. Узловые точки. Каждый элемент описывается множеством характерных точек, называемых узловыми точками или узлами для краткости. Узлы предназначены для описания геометрии элемента и для задания физических степеней свободы (числа неизвестных функций). Узлы обычно находятся в угловых или крайних точках элемента, но могут быть также расположены между угловыми узлами и внутри элемента. Данное различие связано с порядком аппроксимации, который обеспечивает данный конечный элемент. Элементы, имеющие только угловые узлы, называются линейными и обеспечивают линейную интерполяцию геометрии и функций. Элементы, имеющие дополнительные узлы на своих границах между угловыми точками, могут обеспечивать квадратичную или даже кубичную интерполяцию (Рис. 3.1). В первом случае такие элементы называются квадратичными. Отметим также, что существуют элементы, имеющие внутренние узлы. Теоретически такие элементы обеспечивают более точное описание геометрии тела и искомых функций, однако широкого распространения данный тип элементов не получил. При наличии современных автоматических генераторов конечно-элементных сеток часто бывает проще и удобнее разбить конструкцию на большое число линейных элементов простой формы, чем использовать элементы высокого порядка, требующие для построения сетки значительной работы вручную. Элементы, не имеющие внутренних узлов, относятся к так называемому серендипову семейству.

3. Геометрия элемента. Геометрия элемента определяется расположением узловых точек. Большинство элементов, используемых в расчетах, имеют достаточно простую геометрическую форму. Например, в одномерном случае элементы обычно представляют собой прямолинейные отрезки или сегменты кривых линий; в двумерном случае элементы имеют трехстороннюю или четырехстороннюю форму; в трехмерных задачах наиболее распространены такие геометрические фигуры, как тетраэдры, призмы и гексаэдры (Рис. 3.1).

4. Степени свободы. Степени свободы определяют физическое состояние элемента, т.е. физическое поле, которое описывает данный элемент. Благодаря общим степеням свободы в соседних элементах осуществляется сборка модели и формирование глобальной системы конечно-элементных уравнений. В качестве степеней свободы могут фигурировать как узловые значения неизвестной функции, так и ее производные по пространственным координатам в узлах. В первом случае элементы относятся к типу лагранжевых элементов; во втором случае – типу эрмитовых элементов. Например, в простейшей задаче о растяжении стержня неизвестной функцией является продольное перемещение стержня. Соответственно в качестве степеней свободы выступают узловые значения данной функции и, следовательно, конечный элемент относится к лагранжевому типу. Наоборот, в задаче об изгибе стержня неизвестной функцией является поперечное перемещение центральной оси стержня, а в качестве степеней свободы используются как узловые значения самой функции, так и ее производной по продольной координате. Физический смысл этой производной – угол поворота поперечного сечения стержня. Таким образом, конечный элемент, применяемый в расчетах стержня на изгиб, относится к типу эрмитовых элементов. Заметим также, что данные обозначения происходят от названия полиномов Лагранжа и Эрмита, широко используемых в прикладной математике для интерполяции функций по узловым значениям.

5. Узловые силы. Система узловых сил полностью соответствует степеням свободы элемента и выражается с помощью глобального вектора узловых сил.

6. Определяющие соотношения. Для конечных элементов, используемых в механических расчетах, определяющее соотношение задает поведение материала, из которого изготовлена конструкция. Например, в качестве такого соотношения во многих случаях используется обобщенный закон Гука, связывающий тензор деформаций и тензор напряжений в точке. Для линейного упругого стержневого элемента достаточно задать один модуль Юнга Е и один коэффициент температурного расширения ?.

7. Свойства сечения. К свойствам сечения относятся площади и моменты инерции одномерных и двумерных конечных элементов, таких как балки, стержни, пластины. В эту группу также входит толщина пластин и оболочек. При построении конечного элемента свойства сечений считаются заданными и входят в результирующую матрицу жесткости элемента.

Классификация конечных элементов, используемых в механике

1. Простейшие конструкционные элементы. К простейшим структурным элементам относятся элементы типа стержень, балка, труба, брус, панель, работающая на сдвиг (Рис. 3.2). Уравнения, описывающие данные элементы, выводятся из теоретических положений сопротивления материалов, т.е. из упрощенных механических формулировок. Исторически первыми стали использоваться именно эти типы конечных элементов.

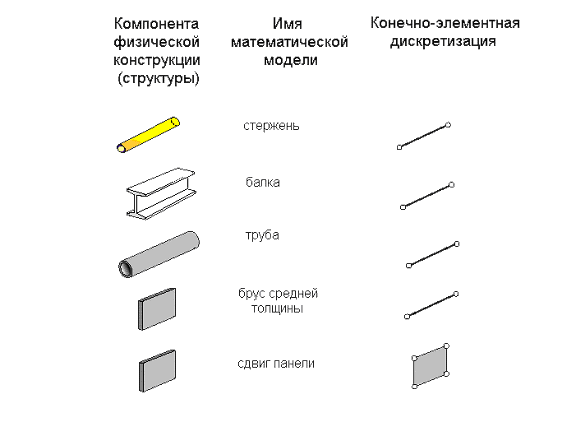
Рис. 3.2. Простейшие конструкционные элементы.

2. Континуальные элементы. Континуальные элементы представляют собой конечные объемы или площади сплошной среды (континуума). Например, к континуальным элементам относятся пластины, оболочки, осесимметричные элементы, трехмерные твердотельные элементы (Рис. 3.3). Уравнения, описывающие данный тип конечных элементов, получаются из общих соотношений механики сплошной среды и, в частности, теории упругости.

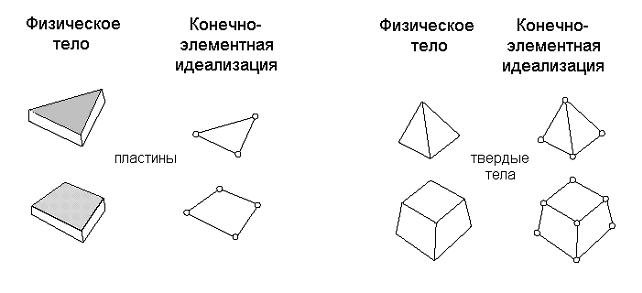
Рис. 3.3. Континуальные конечные элементы.

3. Специальные элементы.Специальные элементы обладают свойствами как конструкционных, так и континуальных элементов. Они выводятся из уравнений механики сплошной среды, но включают в себя некоторые особенности непосредственно связанные с физическими особенностями решаемых задач. В качестве примера можно привести следующие специальные элементы: элемент с трещиной для задач механики разрушения; многослойная панель; бесконечные и полубесконечные элементы; контактные и штрафные элементы; абсолютно твердотельные элементы (Рис. 3.4).

Рис.3.4. Специальные конечные элементы.

4. Макроэлементы.Макроэлементы представляют собой более сложный тип конечных элементов. Как правило, они получаются путем сборки из более простых конструкционных элементов. Число таких элементов, входящих в макроэлемент, как правило, невелико (Рис. 3.5).

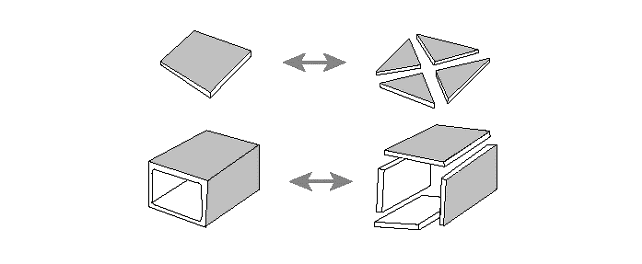
Рис.3.5. Макроэлементы.

5. Подструктуры. Подструктуры можно определить как макроэлементы с явно выраженными структурными особенностями или функциями. Как правило, они получаются путем разделения полной конструкции на функциональные компоненты. Например, крылья и фюзеляж самолета, пролет и тросы подвесного моста. Заметим, что различия между понятиями полной конструкции, подструктур и макроэлементов не всегда очевидны и четко определены. Поэтому часто используется понятие суперэлемента как обобщенного названия для всех типов макроэлементов или подструктур, представляющих собой комбинацию простейших конструкционных элементов.

Ансамблирование

Ансамблирование или сборка представляет собой объединение отдельных элементов в конечно-элементную сетку. С математической точки зрения ансамблирование состоит в объединении матриц жесткости отдельных элементов в одну глобальную матрицу жесткости всей конструкции. При этом существенно используются две системы нумерации узлов элементов: локальная и глобальная. Локальная нумерация представляет собой фиксированную нумерацию узлов для каждого типа конечных элементов в соответствии с введенной локальной системой координат на элементе. Глобальная нумерация узлов всей конструкции может быть совершенно произвольной, также как и глобальная нумерация конечных элементов. Однако, между локальными номерами и глобальными номерами узлов существует взаимнооднозначное соответствие, на основе которого и формируется глобальная система конечно-элементных уравнений.

Граничные условия

Согласно терминологии математической физики, рассматривающей различные дифференциальные уравнения, описывающие физические поля, с единой математической точки зрения, граничные или краевые условия для данных дифференциальных уравнений делятся на два основных типа: существенные и естественные. Обычно, существенные условия накладываются на искомую функцию, а естественные на ее производные по пространственным координатам. В математической физике естественные граничные условия получаются «естественным» образом вместе с исходными дифференциальными уравнениями (уравнениями Эйлера) из соответствующего вариационного принципа, в то время как существенные граничные условия должны выполняться независимо.

С позиции метода конечных элементов существенные граничные условия – это такие, которые непосредственно влияют на степени свободы модели и накладываются на компоненты глобального вектора неизвестных U. Наоборот, естественные граничные условия – это такие, которые опосредованно влияют на степени свободы через глобальную систему конечно-элементных уравнений и накладываются на правую часть системы – вектор F.

В задачах механики, как правило, к существенным граничным условиям относят те, которые включают в себя перемещения (но не деформации, представляющие собой производные перемещений по пространственным координатам). Согласно терминологии теории упругости такие граничные условия называются кинематическими. Например, заделка и шарнирное опирание в стержневых задачах представляют собой существенные, или кинематические, граничные условия, наложенные на прогиб или продольные перемещения точек стержня. Заметим, что в задаче изгиба стержня к существенным условиям относится также условия, наложенные на первую производную по продольной координате от прогиба стержня, которая имеет механический смысл угла поворота сечения стержня. Тоже можно сказать об углах поворота сечений в теории изгиба пластин.

К естественным граничным условиям в механических приложениях МКЭ относят условия, наложенные на различные внешние силовые факторы, действующие на точки поверхности тела – сосредоточенные силы и моменты в стержневых задачах; распределенные силы в двумерных и трехмерных задачах. Такие ограничения носят название силовых граничных условий.

В постановках задач механики сплошной среды, и в частности теории упругости, широко используются смешанные граничные условия. Это означает, что в данной точке поверхности тела одновременно заданы некоторые компоненты перемещений и поверхностных сил. Например, такие условия возникают при решении геометрически симметричных задач. Если остальные граничные условия и внешние силы также зеркально симметричны относительно некоторой плоскости, то смешенные граничные условия на плоскости симметрии представляют собой равенство нулю нормальных перемещений и равенство нулю касательных сил.

Перечисленные три варианта граничных условий наиболее распространены в чисто механических приложениях МКЭ. Однако, в междисциплинарных приложениях МКЭ, и в частности, при расчете температурных напряжений, граничные условия накладываются на различные физические переменные и зависят от особенностей математической постановки соответствующих задач.

Контрольные вопросы

1. Перечислить атрибуты конечных элементов.

2. Дать классификацию конечных элементов.

3. Дать понятие граничных условий. Перечислить типы граничных условий в задачах механики конструкций

Лекция 4

Постановка плоской задачи теории упругости

Основные понятия

Плоская задача теории упругости является наиболее подходящим примером для демонстрации алгоритма МКЭ применительно к решению многомерных задач механики сплошных сред. Базовые соотношения и особенности алгоритма метода конечных элементов в данном случае существенно отличаются от расчета одномерных задач (растяжения, кручения и изгибы стержней).

В механике конструкций плоский тонкий лист материала называется пластиной. Расстояние между верхней и нижней поверхностью пластины называется толщиной и обозначается через h. Пластина имеет также срединную плоскость, лежащую между двух поверхностей. Направление перпендикулярное срединной плоскости называется трансверсальным. Как правило, глобальная ось z направлена перпендикулярно срединной плоскости, в то время как оси x и y лежат в срединной плоскости, образуя глобальную декартову систему координат (Рис. 4.1). Таким образом, уравнение срединной плоскости имеет вид: z=0.

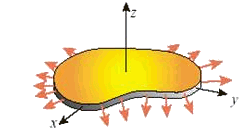
Рис. 4.1. Двумерная конструкция в плоско-напряженном состоянии.

Для того чтобы пластина находилась в плоско-напряженном состоянии, необходимо чтобы выполнялись следующие условия:

1. Все внешние нагрузки: поверхностные, действующие на точки боковой поверхности пластины, и объемные, действующие на внутренние точки пластины, - перпендикулярны оси z, т.е. лежат в плоскости xy, и симметричны относительно срединной плоскости.

2. Все условия закрепления симметричны относительно срединной плоскости.

3. Внутренние перемещения, деформации и напряжения принимаются постоянными по толщине пластины.

4. Нормальные и сдвиговые компоненты тензора напряжений в направлении оси z равны нулю или пренебрежимо малы.

5. Пластина изготовлена из материала, не меняющего своих свойств по толщине. Такие пластины называются трансверсально-однородными.

Заметим, что 3 и 4 предположения не являются необходимым следствием первых двух. Чтобы они выполнялись толщина h должна быть достаточно малой, обычно не более 10% наименьшего характерного размера пластины в срединной плоскости. Кроме того, если толщина пластины изменяется, то это изменение должно быть достаточно плавным. И, наконец, геометрия пластины должна быть симметричной относительно срединной плоскости.

Последнее предположение очевидно исключает из рассмотрения плоские композиционные конструкции, типа ячеистых сотоподобных структур или сендвич-структур. Разработка моделей таких конструкций требует достаточно сложного интегрирования по толщине пластины, а также учета эффектов изгиба и растяжения, и в данном курсе рассматриваться не будет.

Замечание 1. Нагрузка перпендикулярная срединной плоскости приводит к напряженному состоянию, называемому изгибом пластины, описываемому дифференциальным уравнением IV-го порядка относительно прогиба пластины. Алгоритм МКЭ в этом случае имеет принципиально иной характер, поскольку данная задача относится к классу одномерных задач.

Замечание 2. Если принято, что напряжения вдоль оси z имеют место, то состояние пластины носит название обобщенного плоско-напряженного состояния.

Замечание 3. Кроме плоско-напряженного состояния в теории упругости широко применяется понятие плоско-деформированного состояния, согласно которому деформация вдоль оси z равна нулю. Физически это соответствует протяженным конструкциям, нагруженным силами перпендикулярно оси z. Например, плотина, дамба или лопатка ротора генератора при некоторых допущениях.

Математическая модель

Математическая модель пластины в плоско-напряженном состоянии есть двумерная краевая задача теории упругости, заданная в области 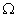с границей Г, как показано на рис. 4.2.

Все основные переменные, входящие в исходные уравнения, представляют собой функции двух переменных x и y и считаются осредненными по толщине пластины. Например, внешние силы, действующие в области 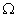и входящие в правую часть уравнения движения точек сплошной среды, есть не что иное, как интегралы по толщине пластины от заданных объемных сил.

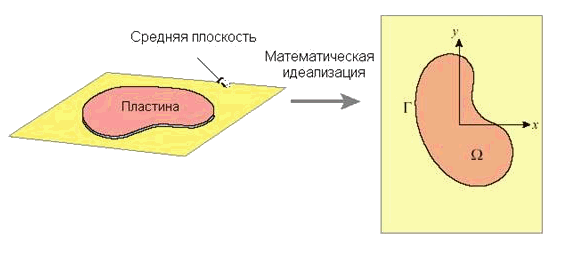
Рис. 4.2. Математическая модель пластины в плоско-напряженном состоянии.

Исходные данные

Исходные данные включают в себя следующие объекты:

Геометрия области. Геометрия тела представляет собой область 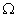с границей Г, показанную на рис. 4.2.

Толщина пластины. Во многих случаях пластины, используемые как конструктивные элементы, имеют постоянную толщину. Если же толщина пластины изменяется, то толщина есть функция двух пространственных координат h=h(x,y), при этом для сохранения плоско-напряженного состояния изменение толщины должно быть достаточно медленным.

Материал пластины. Свойства материала задаются с помощью определяющих соотношений. В данной лекции мы рассмотрим случай линейно упругого, но не обязательно изотропного материала.

Силы, действующие в области 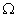. «Областные» силы действуют на внутренние точки области 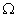. В общем случае они могут быть двух типов. Во-первых, стандартные объемные силы, определенные как силы, действующие на единицу объема пластины, например, вес тела. Во-вторых, специфические областные силы, действующие по касательной к верхней и нижней поверхностям пластины, например, силы трения, которые могут возникать при относительном движении пластины по другому телу. Эти силы определенным образом должны быть приведены к срединной плоскости пластины.

Заданные поверхностные силы. Поверхностные силы – это известные силы, действующие на точки границы Г. Часто они называются поверхностными усилиями. При решении технических задач необходимо обращать внимание на размерность этих сил, т.к. они могут быть заданы как сила на единицу поверхности или как сила на единицу длины.

Кинематические граничные условия. Кинематические граничные условия задают способы закрепления пластины. Точки на границе области могут быть зафиксированы в одном или в двух направлениях. Дополнительно могут быть заданы условия симметрии или антисимметрии. Если кинематические граничные условия не заданы, то такие граничные условия называются свободными.

Искомые функции

В задачах механики основными неизвестными величинами являются поля перемещений, деформаций и напряжений. Согласно ранее сделанным предположениям, все основные искомые физические переменные не зависят от нормальной координаты z и являются функциями только координат x и y.

Перемещения. Вектор перемещений состоит из двух компонент:

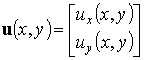
(4.1)

Нормальная компонента перемещений 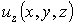в общем случае отлична от нуля из-за эффекта коэффициента Пуассона и зависит от z. Однако это перемещение не входит в разрешающее уравнение задачи и может быть вычислено отдельно по найденным основным компонентам.

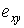Деформации. Деформации, лежащие в плоскости, формируют тензор, определяемый тремя независимыми компонентами: и . Для удобства формулировки конечно-элементных уравнений матричной формы компоненты тензора деформации представим в виде трехкомпонентного «вектора деформации»:

(4.2)

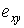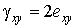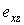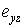Удвоенная компонента представляет собой деформацию сдвига и используется для сокращения записи выражения энергии деформации. Остальные сдвиговые компоненты и равны нулю согласно исходным предположениям. Нормальная компонента 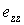обычно не равна нулю из-за эффекта Пуассона. Однако также как перемещение 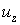нормальная компонента деформации не входит в разрешающее уравнение как неизвестная. В выражении энергии деформации произведение 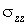обращается в ноль, поскольку нормальное напряжение 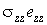равно нулю по исходным предположениям.

Напряжения. Тензор напряжений также определяется тремя независимыми компонентам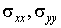и и 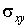, лежащими в плоскости пластины. Как и в случае с деформациями для удобства представления конечно-элементных уравнений в матричном виде сформируем трехкомпонентный «вектор напряжений»:

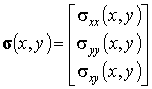
(4.3)

Оставшиеся три компоненты тензора напряжени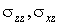й и 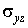равны нулю согласно определению плосконапряженного состояния.

Объемные внутренние силы могут быть получены путем интегрирования напряжений по толщине пластины. В случае однородного распределения напряжений по координате z, данные силы, также образующие тензор, легко могут быть вычислены согласно следующей формуле:

(4.4)

В литературе такие силы часто называются мембранными силами (рис. 4.3.).

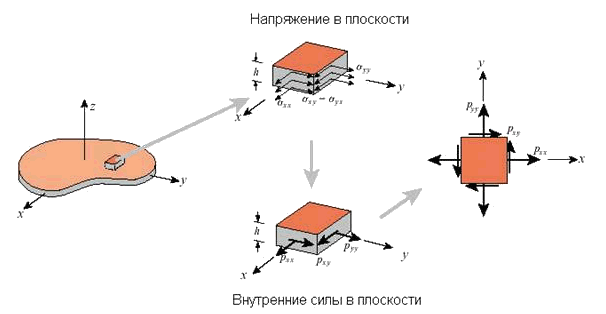
Рис. 4.3. Внутренние силы и напряжения, действующие на произвольный элемент мембраны.

Разрешающие уравнения

Система разрешающих уравнений классической линейной теории упругости схематично представлена на рис. 4.4 в виде так называемой диаграммы Тонти.

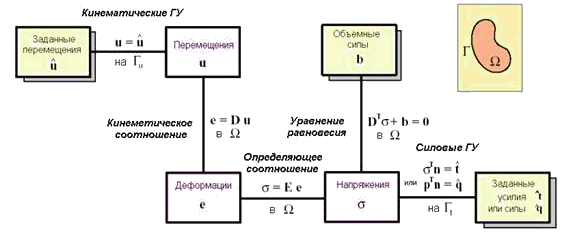
Рис. 4.4. Система разрешающих уравнений классической линейной теории упругости в виде диаграммы Тонти.

Система разрешающих уравнений теории упругости относительно трех неизвестных физических полей перемещений, деформации и напряжений состоит из трех групп уравнений: кинематических соотношений, определяющих уравнений и уравнений равновесия в области тела. При отсутствии начальных напряжений в теле эта система уравнений может быть записана в следующем символьно-матричном виде:

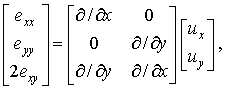
	(4.5а)
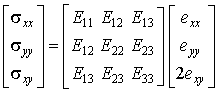
	(4.5б)
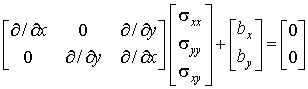
	(4.5в)

Кроме уже введенных матричных векторов перемещений, деформаций и напряжений, записанная система трех матричных уравнений содержит вектор объемных сил с компонентами b_x, b_y, входящий в уравнение равновесия, матрицу упругих модулей с компонентами E_ij, связывающую напряжения и деформации в точке тела, а также две символические матрицы, состоящие из частных производных по пространственным координатам. Заметим, что символические матрицы, входящие в кинематическое соотношение и в уравнение равновесия, совпадают с точностью до операции транспонирования.

В матричном виде система (4.5) может быть представлена в следующем виде:

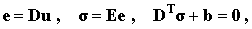
(4.6)

где E–симметричная матрица упругих модулей, D – символическая матрица, состоящая из частных производных, b– матричный вектор объемных сил.

Заметим, что приведенная система уравнений (4.6) несколько отличается от координатной или тензорной форм записи полной системы уравнений теории упругости, часто используемым в литературе. Достоинство данной формулировки состоит в том, что все уравнения уже записаны в матричном виде, наиболее удобном для вывода соотношений метода конечных элементов.

Если материал пластины является изотропным, то как известно из теории упругости компоненты матрицы упругих модулей E могут быть выражены через технические константы материала: модуль упругости E, коэффициент Пуассона и модуль сдвига G:

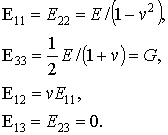
При этом напомним, что только две из перечисленных технических констант являются независимыми. Формула, связывающая модуль упругости E, коэффициент Пуассона и модуль сдвига G, имеет следующий вид:

.

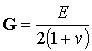Граничные условия

В классической задаче теории упругости граничные условия, заданные на поверхности Г, могут быть двух типов: кинематические граничные условия и силовые граничные условия. Предполагается, что каждый тип граничных условий задан на своей части поверхности: Г_u и Г_t соответственно (Рис. 4.5).

Рис. 4.5. Кинематические и силовые граничные условия в плоской задаче теории упругости.

Кинематические граничные условия заданы на части поверхности Г_u и могут быть записаны в следующей формуле: