Общие понятия и классификация задач вычислительной механики
Механика как фундаментальная научная дисциплина может быть подразделена на три основные части:
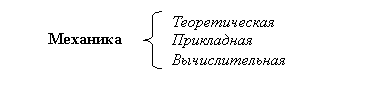
Теоретическая механика имеет дело с фундаментальными законами и принципами, описывающими механическое движение абсолютно твердых и деформируемых тел. Прикладная механика на основе теорем теоретической механики занимается построением математических моделей физических явлений, формулировкой и решением научно-исследовательских и инженерных задач. Вычислительная механика решает специфические задачи путем математического моделирования с помощью численных методов, реализованных на цифровых вычислительных машинах.
ЗАМЕЧАНИЕ
Перефразирую старую шутку о математиках, можно определить механика-расчетчика, как человека, который ищет решения заданных задач; механика-прикладника, как человека, который ищет практические задачи, соответствующие данным решениям; и механика-теоретика, как человека, который доказывает существование задач и их решений.
Вычислительная механика
Области приложений вычислительной механики могут быть выделены в соответствии с физическим масштабом решаемых задач.
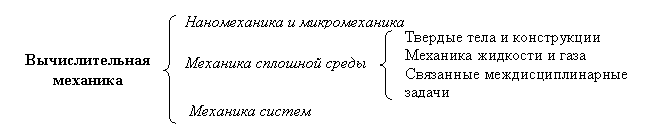
Наномеханика имеет дело с явлениями на молекулярном и атомном уровнях материи и, таким образом, тесно взаимодействует с физикой частиц и химией. Микромеханика в основном рассматривает явления на уровне кристаллов и гранул. Ее основное технологическое приложение – дизайн и производство материалов и микроприборов.
Механика сплошной среды изучает тела на макроскопическом уровне, используя континуальные модели, в которых микроструктура гомогенизируется с помощью феноменологического подхода. Две традиционные области приложения механики сплошной среды – механика жидких и твердых тел; последняя включает механику конструкций, которые, очевидно, изготавливаются из твердых тел. Вычислительная механика твердого тела использует научно-прикладной подход, в то время как вычислительная механика конструкций акцентирует внимание на технологических приложениях к анализу и дизайну конструкций.
Вычислительная механика жидкостей имеет дело с задачами, описывающими равновесие и движение жидкости и газов, включая такие хорошо разработанные области как гидродинамику, аэродинамику, физику атмосферы, физику горения и взрыва.
Механика связанных задач - одна из последних областей приложения численных методов. Подразумевается, что эта область включает физические системы, выходящие за классические границы механики твердых и жидких тел, рассматривает взаимодействие жидкостей и конструкций. Например, фазовые задачи, такие как таяние льда или застывание металла, соответствуют данной категории, поскольку включают взаимодействие механических и электромагнитных явлений.
Наконец, механика систем имеет дело с механическими объектами, естественными или искусственными, проявляющими характерные макроскопические функции. Пример искусственных систем – самолеты, дома, мосты, двигатели, машины, микрочипы, роботы и т.д.; биологических систем – целые животные или деревья, изучаемые с позиций биомеханики. В выше рассмотренной схеме системы представляют собой наиболее общую концепцию, изучаются они путем декомпозиции: поведение отдельных компонент системы плюс взаимодействие между компонентами. В свою очередь компоненты могут быть разложены на более мелкие части и т.д. Продолжая этот иерархический процесс можно получить отдельные компоненты достаточно простые для того, чтобы быть изученными в рамках отдельных дисциплин. Однако взаимодействие между ними может оказаться гораздо более сложным. Соответственно, искусство исследователя состоит в том, чтобы правильно определить, на каком иерархическом уровне системы необходимо остановиться для того, чтобы получить нетривиальный результат.
Статика и динамика
Задачи механики сплошной среды могут быть классифицированы в соответствии с тем, принимается во внимание эффект инерции или нет:
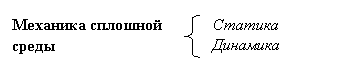
В динамике явно рассматривается зависимость от времени, поскольку вычисление сил инерции (а так же, возможно, демпфирующих сил) требует вычисление производных по времени.
Задачи статики так же могут быть временно зависимыми, однако, силами инерции пренебрегают в силу их малости. Статические задачи могут быть так же подразделены на строго статические и квази-статические. В математическую формулировку последних время явно не входит; вместо него в случае необходимости используются временно подобный параметр, характеризующий историю процесса. В других квази-статических задачах, таких как расчет деформации ползучести, циклическая усталость, пластичность, зависящая от скорости нагружения, требуется более реалистичная оценка времени, однако, и в этом случае инерциальные силы пренебрежимо малы.
Линейность и нелинейность
Задачи механики могут быть так же подразделены на линейные и нелинейные:
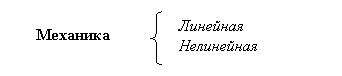
Линейная механика имеет дело с проблемами, в которых отклик системы линеен в причинно-следственном смысле. Например, если приложенные внешние силы удваиваются, то результирующие перемещения и внутренние напряжения так же удваиваются. В противоположном случае задачи классифицируются как нелинейные.
Методы дискретизации
Последняя классификация задач вычислительной механики базируется на методе дискретизации, с помощью которого непрерывная математическая модель преобразуется в дискретную модель, состоящую из конечного числа степеней свободы:
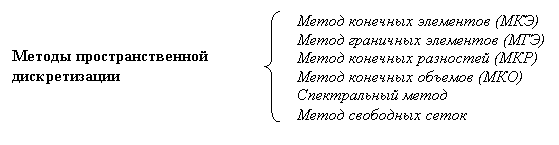
В настоящее время в линейной механике твердого тела метод конечных элементов наиболее распространен, в то время как применение метода граничных элементов для решения данных задач находится на втором месте. Для нелинейных задач метод конечных элементов является наиболее эффективным и доминирующим.
Классический метод конечных разностей почти полностью потерял свое значение при решении практических задач механики твердого тела. Это утверждение, однако, не верно для механики жидкости и газов, где разностные методы до сих пор широко распространены. Метод конечных объемов, основанный на законах сохранения, применяется для решения сильно нелинейных задач механики жидкости и газов. Спектральные методы используются в различных областях механики и основаны на пространственно-временном преобразовании в область, где задача может быть легко решена. Метод свободных сеток – один из новых методов вычислительной математики и основан на конечно-разностном подходе с использованием независимых сеток, полученных в результате применения конечно-элементных технологий.
Варианты МКЭ
Термин Метод Конечных Элементов в действительности определяет широкий спектр вычислительных технологий в соответствии с некоторыми общими свойствами, которые будут рассмотрены в дальнейшем. Классификация МКЭ применительно к механике конструкций в зависимости от типа искомой функции может быть представлена следующим образом:
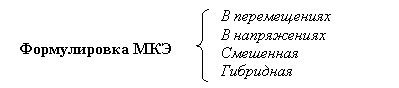
Различие между этими формулировками проистекает из вида вариационного принципа, используемого для построения алгоритма МКЭ, и, соответственно, из вида искомой функции:

Процесс конечно-элементного анализа
Процесс конечно-элементного анализа включает определенную последовательность шагов. Эта последовательность имеет две канонические конфигурации в зависимости от окружения, в котором используется МКЭ:
· Математический подход
· Физический подход.
Схема математического подхода изображена на рис. 1.1. В центре данного подхода находится математическая модель. Обычно это есть обыкновенное дифференциальное уравнение или уравнение в частных производных по пространственным координатам и времени. Дискретная конечно-элементная модель генерируется путем применения какого-либо вариационного принципа к исходной системе дифференциальных уравнений или же метода взвешенных невязок в его ослабленном варианте. Этот шаг называется дискретизацией. Получаемая система конечно-элементных уравнений решается одним из методов прикладной математики решения больших систем алгебраических уравнений. В результате чего получается так называемое дискретное, или приближенное, решение.
Идеальная физическая система в данном случае может быть представлена как реализация математической модели; и наоборот, математическая модель есть идеализация этой системы. Например, если математическая модель есть уравнение Пуассона, то его реализацией может быть проблема распределения электростатического заряда или распределение тепла. В принципе этот шаг не существенен и может быть опущен. Другими словами, конечно-элементная дискретизация может быть приведена и без обращения к физике явления.
Концепция ошибки, или погрешности, возникает, когда приближенное решение подставляется в математическую модель. Эта подстановка называется верификацией. Полная ошибка численного подхода включает в себя ошибку решения системы алгебраических уравнений и погрешность дискретизации. Подстановка приближенного решения в идеальную физическую систему, т.е. проведение теста или опыта, в принципе могла бы дать оценку этой ошибки моделирования. Однако, в концепции математического подхода МКЭ физическая система не играет большой роли и является лишь некоторым идеализированным образом математической модели.
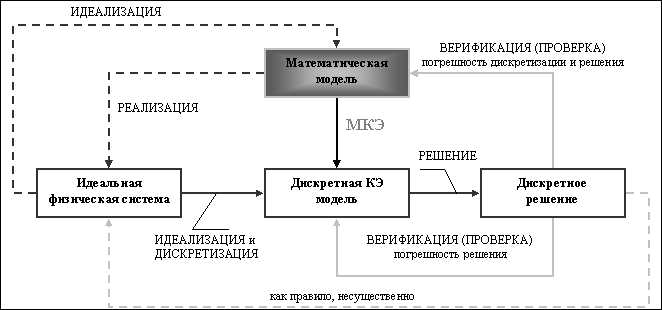
Рис. 1.1 Математическая концепция МКЭ
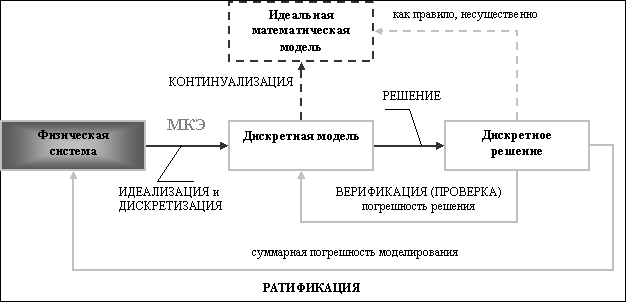
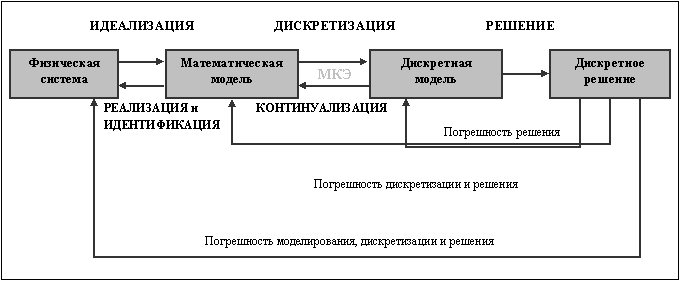
Схема физического подхода изображена на рис. 1.2. Центральным звеном в этом случае является физическая система, которая должна быть рассчитана. Процедуры идеализации и конечно-элементной дискретизации проводятся одновременно, чтобы получить дискретную модель. Приближенное дискретное решение получают аналогично предыдущему.
Идеальная математическая модель в данном подходе может быть представлена как предельный переход или «континуализация» дискретной модели. Для определенных физических систем, которые хорошо моделируются непрерывными полями, этот шаг существенен, для других, таких как сложные инженерные системы, подобный переход не имеет большого смысла. Для них конечно-элементная модель может быть построена без обращения к математическим моделям только на основе экспериментальных измерений.
Понятие погрешности, или ошибки, возникает в физическом подходе благодаря двум процедурам – верификации численного решения и оценки результатов моделирования (ратификации). Верификация имеет тот же смысл, что и в математическом подходе: численное решение подставляется в дискретную модель, в результате чего получается погрешность решения. Подстановка приближенного решения в идеальную математическую модель, в принципе, может дать ошибку дискретизации. Однако это редко используется в сложных инженерных системах, поскольку, как правило, в данном случае математической модели не существует, и сравнивать полученное решение необходимо с исходной физической системой. Таким образом, оценка или ратификация численного решения основана на сравнении результатов моделирования с экспериментальными данными, что и дает суммарную погрешность моделирования.
 M
M
Рис. 1.2. Физическая концепция МКЭ.
Один из способов настройки дискретной модели, для того чтобы она лучше соответствовала физической системе, называется уточнением модели (Рис. 1.3). Имеющиеся свободные параметры модели определяются путем сравнения дискретного приближенного решения с результатами эксперимента, как показано на рис. 1.3. Поскольку, условия минимизации ошибки моделирования, как правило, нелинейные (даже если конечно-элементная модель линейная), то процесс уточнения является существенно итерационным.
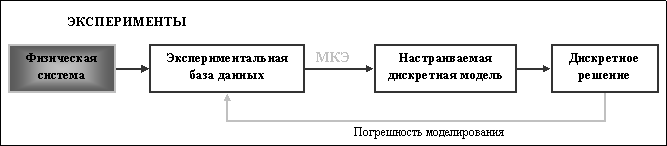
Рис. 1.3. Процесс уточнения дискретной модели.
Выше рассмотренные подходы применения МКЭ не являются взаимоисключающими, а дополняют друг друга. Исторически физический подход был первым для разработки конечно-элементных моделей очень сложных инженерных систем, таких как самолеты, корабли и т.п. Математический подход возник позднее и среди прочих вещей призван обеспечить необходимый теоретический фундамент МКЭ, для того чтобы распространить метод на решение различных междисциплинарных задач выходящих за рамки общепринятого прочностного анализа конструкций.
Контрольные вопросы
1. Что изучает вычислительная механика?
2. Объяснить понятие математической концепции МКЭ.
3. Объяснить понятие физической концепции МКЭ. В чем между ними разница?
Лекция 2
Основные понятия и концепция МКЭ
Терминология
Классическая аналитическая механика была разработана Эйлером и Лагранжем в конце 18 века и впоследствии развита Гамильтоном и Якоби, как систематическая формулировка механики Ньютона. Объектами изучения аналитической механики являются модели механических систем от отдельных частиц, состоящих из достаточно большого числа молекул, до сложных инженерных конструкций и тел солнечной системы. Пространственная конфигурация любой из таких систем описывается числом степеней свободы системы, или другими словами, обобщенными координатами. В математически ориентированных курсах для их обозначения используются так же термины переменные состояния и главные переменные.
Если число степеней свободы модели конечно, модель называется дискретной, и непрерывной (континуальной) в противном случае.
Поскольку МКЭ представляет собой один из методов дискретизации, то число степеней свободы конечно-элементной модели необходимо конечно. Обычно, все степени свободы собираются в матричный вектор, обозначаемый Uи называемый вектором степеней свободы или вектором состояния. Термин вектор узловых перемещений обычно используется в механических приложениях.
В аналитической механике каждой степени свободы соответствует сопряженная переменная, представляющая собой обобщенную силу. В немеханических приложениях также существует подобное множество сопряженных переменных, которые для универсальности называются силами или силовыми переменными. Эти силы объединяются в матричный вектор, обозначаемый F. Отметим, что внутреннее произведение вектора сил на вектор степеней свободы имеет смысл внешней энергии или работы.
Предполагается, что соотношение между U и F является линейным и однородным. Последнее означает, что если U стремится к нулю, то и F стремится к нулю, в этом случае соотношение между ними выражается следующим основным уравнением:
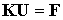
| (2.1) |
Kдляуниверсальности называется матрицей жесткости, даже в случае нечисто механических приложений, поскольку к настоящему времени нет общего соглашения по обозначению этой матрицы в различных дисциплинах.
Физический смысл векторов U и F изменяется в зависимости от области приложения МКЭ, как это показано в таблице 2.1.
Таблица 2.1. Физический смысл векторов U и F в различных конечно-элементных приложениях
| Область приложения | Вектор состоянияU | Сопряженный вектор F |
| Механика конструкций и твердых тел | Перемещение | Механическая сила |
| Теплопроводность | Теплопроводность | Тепловой поток |
| Потенциальное течение | Давление | Скорость частицы |
| Общий вид течения | Скорость | Поток |
| Электростатика | Электрический потенциал | Плотность заряда |
| Магнитостатика | Магнитный потенциал | Интенсивность магнитного поля |
Заметим, что если соотношение между силами и перемещениями линейное, но неоднородное, уравнение 2.1 обобщается на следующее соотношение:
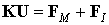
| (2.2) |
Здесь 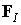 есть узловой вектор начальных сил, который возникает, например, при решении задач термоупругости для учета начальных температурных напряжений;
есть узловой вектор начальных сил, который возникает, например, при решении задач термоупругости для учета начальных температурных напряжений; 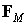 - вектор механических сил.
- вектор механических сил.
Основные шаги МКЭ
Основные шаги МКЭ показаны на рис. 2.1. Схематично их можно назвать следующим образом:
· Идеализация
· Дискретизация
· Решение.
2.1. Основные шаги численного моделирования
Идеализация
Под идеализацией понимают процесс перехода от исходной физической системы к математической модели. Этот процесс является наиболее важным шагом при решении технической или инженерной задачи.
Ключевым пунктом в этом процессе является понятие модели, которую можно определить как символическое устройство, построенное для моделирования и предсказания поведения системы. Математическое моделирование, или идеализация, есть процесс, с помощью которого инженер переходит от реальной физической системы к математической модели системы. Данный процесс называется идеализацией, поскольку математическая модель необходимо абстрагируется от физической реальности.
В качестве примера реальной физической системы рассмотрим инженерную конструкцию в виде плоской пластины, нагруженную поперечными силами. Математические модели данной системы, которые инженер может использовать для анализа напряжений в пластине, могут быть следующими:
1. Модель очень тонкой пластины, основанная на теории изгиба мембран.
2. Модель тонкой пластины, основанная на классической теории Кирхгоффа.
3. Модель достаточно толстой пластины, основанная, например, на теории Миндлина-Рейсснера.
4. Модель очень толстой пластины, основанная на трехмерной теории упругости.
Очевидно, инженер должен обладать достаточными теоретическими знаниями, чтобы правильно выбрать соответствующую математическую модель системы (конструкции), которую ему необходимо исследовать.
Явное и неявное моделирование
Как было отмечено, диаграмма на рис. 2.1 представляет собой упрощенную схему инженерного процесса. В обобщенном виде он представлен на рис. 2.2.
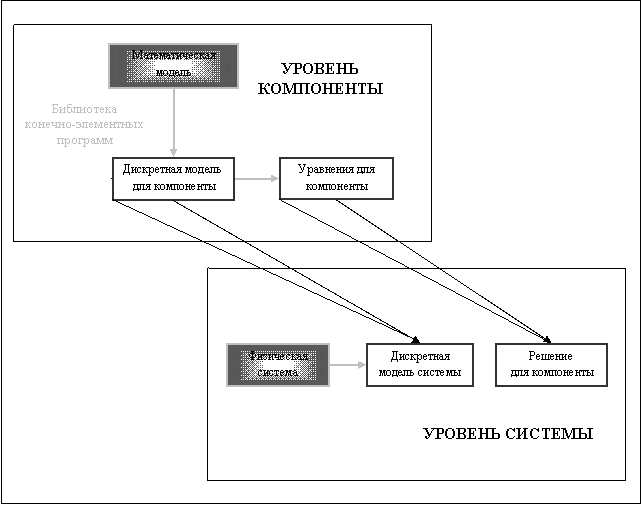
Рис. 2.2. Общий вид инженерного процесса.
Рассмотрим современный сценарий действий инженера-механика в крупной компании. Предположим, необходимо рассчитать некоторую техническую конструкцию с помощью некоторого коммерческого универсального конечно-элементного комплекса. Как правило, любой коммерческий пакет предлагает широкий каталог различных типов элементов. Например, стержневые, балочные, оболочечные, осесимметричные, трехмерные и т.д. В момент выбора того или иного элемента из каталога инженер автоматически принимает некоторую математическую модель, на которой этот элемент основан. Это называется безусловным моделированием. В идеале инженер должен быть полностью компетентен в принятии решения. Обеспечение выпускника подобной «конечно-элементной грамотностью» есть одна из целей данного курса.
Под явным моделированием понимается подход, когда выбору математической модели уделяется значительное внимание. При этом приобретаются специализированные конечно-элементные программы, реализующие данную модель, или же такие программы пишутся самостоятельно. Очевидно, данные подход требует гораздо больше знаний, опыта и ресурсов, чем безусловное моделирование. Однако, для многих задач, которые не могут быть решены с помощью общего подхода, явное моделирование является единственным способом решения. Заметим, что на практике часто используются комбинации обоих подходов.
Дискретизация
Математическое моделирование есть первый упрощающий шаг при решении реальных инженерных задач. Однако, математические модели физических систем вовсе необязательно просты для решения. Они часто описываются связанными системами уравнений в частных производных по пространству и времени и сложными граничными условиями. Такие модели имеют бесконечное число степеней свободы.
Решение полученных уравнений может быть аналитическим или численным. Аналитические решения, называемые также решениями в замкнутой форме, могут быть применены к широкому классу задач, поскольку, выражаются в символической форме. Однако, к сожалению, возможность их получения ограничена простыми уравнениями, регулярными областями и постоянными граничными условиями.
Поскольку, большинство проблем, стоящих перед инженером не может быть решено аналитически или требуют для этого непропорционально больших усилий, то единственной альтернативой является применение численного моделирования.
Для того, чтобы численное моделирование могло быть применено на практике необходимо уменьшение числа степеней свободы до конечного значения. Этот процесс называется дискретизацией. Результатом процесса дискретизации является дискретная модель. Для сложных инженерных систем эта модель есть результат многоуровневой декомпозиции. Отметим, что дискретизации могут подвергаться как пространственные координаты, так и время. Соответственно, выделяют пространственную дискретизацию и временную.
Источники ошибки и аппроксимация
Как показано на рис. 2.1, каждый шаг численного моделирования вносит свою ошибку. В инженерной практике погрешность перехода от физической модели к математической является одной из наиболее существенной. Однако, ошибки этого шага достаточно трудны и дорогостоящи для оценки, поскольку, верификация модели требует доступа и сравнения с экспериментальными данными, объем которых часто недостаточен или же они вообще отсутствуют в случае новых инженерных продуктов.
Следующая по важности идет ошибка дискретизации. Даже, если ошибка этапа решения дискретной модели игнорируется, полученное численное решение, в общем, является лишь аппроксимацией, или приближением, точного решения математической модели. Тем самым мы получаем ошибку, или погрешность, дискретизации. Изучением свойств и поведения этой ошибки занимается раздел прикладной математики, называемый теорией аппроксимаций.
Интуитивно можно ожидать, что точность решения дискретной модели должна улучшаться при увеличении числа степеней свободы модели и, следовательно, ошибка дискретизации стремится к нулю при стремлении числа степеней свободы к бесконечности. Данное утверждение описывает так называемое требование сходимости приближенного решения. Однако доказательство этого утверждения не всегда возможно и является одной из ключевых целей теории аппроксимаций.
Общая схема алгоритма МКЭ
Последовательность процедур алгоритма МКЭ может быть представлена в следующем виде:
1.Дискретизация рассматриваемой области, т.е. замена континуальной среды совокупностью КЭ заданной формы, соединенных между собой в узлах конечным числом связей.
Этот этап, несмотря на видимую простоту, имеет важное значение, хотя он и не обусловлен строгими теоретическими рекомендациями и во многом определяется интуитивно. Обычно при построении конечно-элементной модели руководствуются предварительными представлениями о характере ожидаемого результата, и в местах высоких градиентов искомых величин сетку конечных элементов сгущают.
Дата добавления: 2015-06-17; просмотров: 2979;
