Определение деформаций и напряжений. 2 страница

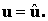
(4.7)

Правая часть соотношения (4.7) представляет собой заданные перемещения точек поверхности. Во многих случаях эти перемещения равны нулю. Например, в случае, если часть поверхности каким-либо образом закреплена, как показано на рис. 4.5.

Силовые граничные условия заданы на части поверхности Г_t и могут быть записаны в следующей форме:

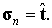
(4.8)

В формуле (4.8) правая часть представляет собой заданные поверхностные силы или поверхностные усилия, а левая часть – вектор напряжений на площадке с нормалью n.

Альтернативная форма записи силовых граничных условий может быть записана в виде:

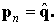
(4.9)

где 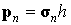и .

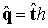Вектор напряжений на площадке с нормалью nопределяется согласно формуле Коши через компоненты внешней нормали к поверхности и компоненты тензора упругости в точке поверхности:

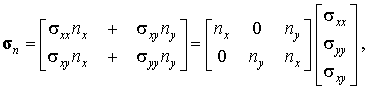
(4.10)

где n_x и n_y обозначают декартовы координаты единичной нормали к поверхности n^(e) (направляющие косинусы). Таким образом (4.8) может быть записано в виде двух скалярных соотношени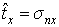й и .

В некоторых случаях бывает удобно записать условие (4.8) в локальной системе координат, образованной нормалью n<B< i>> иортом касательной t:

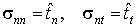
(4.11)

где соответствующие компоненты напряжений в локальной системе координат могут быть выражены следующим образом:

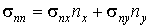
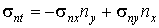
Контрольные вопросы

1. Дать определение плоско-напряженного и плоско-деформированного состояния.

2. Записать общую систему уравнений плоской задачи теории упругости.

3. Записать граничные условия плоской задачи теории упругости.

Лекция 5

Конечно-элементная формулировка плоской задачи теории упругости: базовые соотношения

Ослабленная формулировка задачи теории упругости

Задачи математической физики могут быть поставлены различным образом. Принято различать три основные формулировки краевых задач математической физики и в частности задачи теории упругости:

1. Прямая (строгая) формулировка, представляющая собой исходную систему дифференциальных уравнений;

2. Ослабленная формулировка, выражаемая в виде некоторого вариационного принципа;

3. Обратная формулировка, в которой исходное уравнение задачи выражено в виде некоторого интегрального уравнения.

Диаграмма Тонти представленная в прошлой лекции на рис. 4.4 представляла собой прямую формулировку задач теории упругости. Все соотношения между физическими переменными в данном случае должны выполняться в каждой точке тела. Это строгое условие схематично выражено черными линиями на диаграмме (рис.4.4).

Ослабленная формулировка изображена на рис. 5.1. Схематично она может быть получена путем ослабления одного или более строгого соотношения. На рис. 5.1 такие ослабленные соотношения изображены серыми линиями. Ослабленные соотношения означают, что соответствующие уравнения выполняются не в каждой точке тела, а в среднем, т.е. в некотором интегральном смысле. Ослабленные связи обеспечиваются с помощью некоторых вариационных формулировок, подходящих для данной задачи. Заметим, что, в общем, для одной и той же задачи может быть сформулирован не один вариационный принцип, и, следовательно, может быть составлено множество ослабленных формулировок задачи. В противоположность этому прямая, или строгая, формулировка всегда единственна.

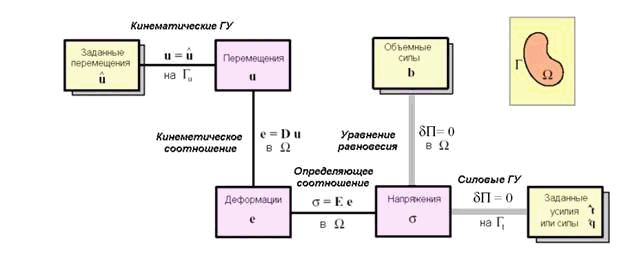
Рис. 5.1. Ослабленная формулировка задач теории упругости в виде диаграммы Тонти.

На рис. 5.1 представлена ослабленная формулировка плоской задачи теории упругости, связанная с вариационным принципом минимума полной потенциальной энергии тела. Согласно данной формулировке уравнение равновесия в области и силовые граничные условия на части поверхности Г_t выполняются в ослабленном смысле как вариационные соотношения принципа минимума полной потенциальной энергии 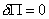, где функционал энергии П будет подробно рассмотрен ниже. Соответствующие связи выражены серыми линиями. Формулировка метода конечных элементов в перемещениях основывается на данной ослабленной формулировке задачи.

Полная потенциальная энергия тела

Функционал полной потенциальной энергии идеально упругого тела определяется следующей формулой:

.

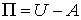(5.1)

В соотношении (5.1) U есть внутренняя энергия деформации тела, вычисляемая как интеграл по объему тела от удельной энергии деформации тела, равной половине матричного произведения вектора напряжений на вектор деформаций:

.

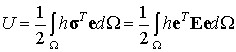(5.2)

Толщина h появляется под знаком интеграла в результате представления объемного интеграла через повторный интеграл по области 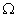и нормальной координате z:

.

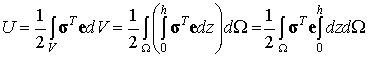Поскольку напряжения и деформации не зависят от координаты z согласно постановке плоской задачи теории упругости, то их произведение может быть вынесено за знак интеграла по толщине пластины h. Заметим, что сама толщина может быть переменной в области пластины, и поэтому полностью за знак интеграла не выносится.

Величина A в формуле (5.1) представляет собой работу внешних объемных и поверхностных сил, заданных соответственно в области 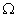и на части поверхности Г_t.:

.

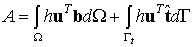(5.3)

Аналогично предыдущему объемный интеграл от объемных сил преобразуется к повторному и затем в результате интегрирования по толщине - к интегралу по области пластины 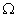. Второй интеграл, представляющий собой работу поверхностных сил, действующих на боковой грани пластины преобразуется сходным образом:

.

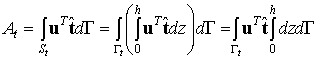Обратим внимание, что в соотношении (5.3) используется интеграл только по части поверхности Г_t, поскольку только на данной части поверхности заданы внешние силы.

Конечно-элементная интерполяция

Согласно основной идее метода конечных элементов область тела 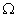представляется в виде множества непересекающихся подобластей, называемых конечными элементами, как показано на рис. 5.2.

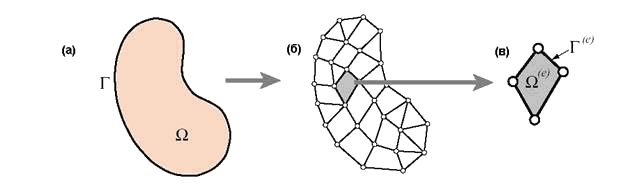
Рис. 5.2. Конечно-элементная дискретизация области тела: (а) – исходная область 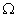с границей Г; (б) – дискретизованная область 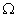, представленная в виде сетки конечных элементов; (в) – конечный элемент, занимающий область 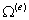с границей Г^(е).

Как правило, для решения плоской задачи теории упругости используются трехсторонние или четырехсторонние конечные элементы, как было отмечено в лекции 3. Каждый конечный элемент определяется набором узлов. В качестве примера на рис. 5.2 приведен четырехсторонний элемент с линейной интерполяцией координат и перемещений, заданный четырьмя узлами. Напомним, что в случае использования квадратичной интерполяции координат или перемещений четырехсторонний элемент должен описываться восемью узлами (Рис. 3.1).

В случае плоской задачи в каждом узле заданы две компоненты перемещений, которые являются искомыми степенями свободы, как говорилось в предыдущих лекциях. Искомые степени свободы, или узловые переменные, принято объединять в так называемые элементные вектора узловых переменных, в данном случае узловых перемещений:

.

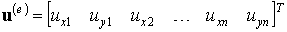(5.4)

Таким образом, каждый элементный вектор содержит 2n степеней свободы, где n – число узлов элемента. В данном случае n=4 (Рис. 5.2), однако, как было показано в лекции 3, число узлов может быть различным в зависимости от типа элемента (Рис. 5.3). Заметим также, что, пронумеровав узлы от 1 до n в пределах данного элемента, мы тем самым ввели локальную нумерацию узлов на элементе. Необходимо отметить, что способ нумерации узлов в пределах элемента может быть произвольным. Однако, один раз выбрав способ нумерации для данного типа элементов, необходимо его придерживаться.

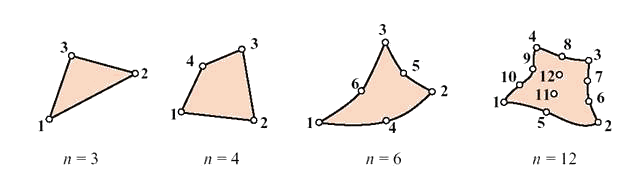
Рис. 5.3. Примеры двумерных конечных элементов, определяемых различным числом узлов.

После выбора узловых переменных необходимо задать закон изменения искомой функции в пределах конечного элемента. Поле перемещений в пределах элемента определяются с помощью интерполирующих соотношений:

,

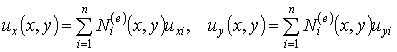(5.5)

где 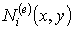- специальные интерполирующие функции, или функции формы элемента.

Эти функции обладают рядом специфических свойств, которые будут рассматриваться в дальнейшем. Одно из основных свойств, которое хотелось бы отметить сейчас – локальность, или финитность, интерполирующих функций, что означает, что эти функции заданы только в пределах данного элемента. Заметим также, что функции формы играют значительную роль в алгоритме метода конечного элемента, поскольку задают порядок интерполяции искомых переменных.

Минимальное условие, которое должно быть наложено на функции 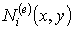, то, что каждая функция 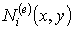должна принимать единичное значение в узле i элемента, и обращаться в ноль в остальных узлах.

В матричной форме интерполирующие соотношения (5.5) могут быть записаны следующим образом:

,

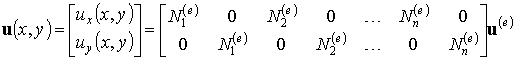(5.6а)

откуда получаем:

.

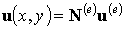(5.6б)

В соотношениях (5.6а) и (5.6б) 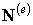представляет собой матрицу интерполирующих функций размерности 2x2n, поскольку мы рассматривает двумерную задачу. В случае трехмерной задачи теории упругости соответствующая матрица интерполирующих функций имела бы размерность 3x3n. При этом вид соотношения (5.6б) не изменился бы. В этом проявляется значительное достоинство метода конечных элементов: основные формулы общего алгоритма остаются справедливыми и не меняют своего вида при анализе различных задач теории упругости.

Соотношение (5.6б) является одним из наиболее важных фундаментальных уравнений метода конечных элементов, поскольку участвует при выводе практически всех формул алгоритма МКЭ. В частности, теперь с помощью данного уравнения мы можем преобразовать кинематическое соотношение (4.5а, лекция 4), входящее в постановку плоской задачи теории упругости и связывающее перемещения и деформации в точке. В матричном виде данное соотношение в произвольной точке конечного элемента может быть записано следующим образом:

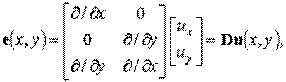
(5.7а)

где D – матрица, состоящая из частных производных интерполирующих функций по пространственным координатам.

Подставляя в соотношение (5.7а) интерполирующее соотношение (5.6б), получим:

,

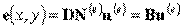(5.7б)

где 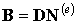- представляет собой матрицу размерности 3x2n, называемую матрицей градиентов.

Явное выражение матрицы градиентов может быть получено, если мы перемножим матрицу 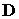размерности 3x2 на матрицу 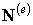размерности 2x2n. В результате получим:

.

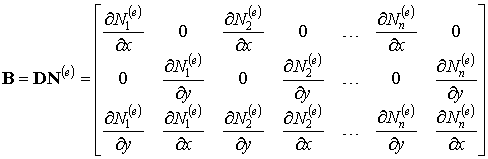(5.8)

В развернутом виде выражение деформации в точке, таким образом, может быть записано в виде:

.

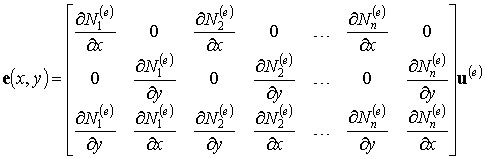(5.9)

Заметим, что матрица градиентов, также как и матрица интерполирующих функций зависит от номера элемента e. В данном случае индекс e опущен только для сокращения записи.

После определения вектора деформации в точке можно вычислить и вектор напряжений согласно формуле (4.5б). В матричном виде она может быть представлена следующим образом:

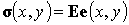
(5.10)

Данное соотношение выполняется во всех точках конечного элемента и поэтому вместо вектора деформации 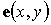может быть подставлено его выражение (5.7б). В результате получим:

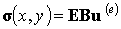
(5.11)

Таким образом, пользуясь основным интерполяционным соотношением МКЭ, мы получили необходимые выражения векторов деформаций и напряжений в произвольной точке произвольного конечного элемента. Эти формулы существенным образом будут использованы в следующей лекции при выводе разрешающих уравнений метода конечных элементов применительно к плоской задаче теории упругости.

Контрольные вопросы

1. Дать понятие ослабленной формулировки задачи теории упругости.

2. Записать выражение полной потенциальной энергии тела. Пояснить входящие в него величины.

3. Дать понятие интерполирующих соотношений и матрицы градиентов.

Лекция 6

Конечно-элементная формулировка плоской задачи теории упругости: вывод СЛАУ МКЭ

Принцип минимума потенциальной энергии

Согласно вариационному принципу Лагранжа полная потенциальная энергия тела, находящегося в равновесии под действием внешних объемных и поверхностных сил, достигает минимума на истинном поле перемещений, т.е. на поле перемещений, удовлетворяющем полной системе уравнений теории упругости. Отсюда следует, что вариация функционала энергии на истинных перемещениях должна быть равна нулю:

.

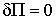(6.1)

Поскольку полная потенциальная энергия тела складывается из потенциальной энергии деформации тела и работы внешних сил (5.1, лекция 5), то последнее соотношение (6.1) может быть записано следующим образом:

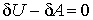
(6.2)

где 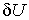- вариация потенциальной энергии деформации тела, 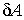- вариация работы внешних сил, совпадающая по своему виду с элементарной работой внешних сил на возможных перемещениях.

Вычислим первое слагаемое в формуле (6.2). В предыдущей лекции было отмечено, что потенциальная энергия деформации тела представляет собой интеграл по объему тела от удельной потенциальной энергии:

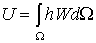
(6.3)

где W – удельная потенциальная энергия тела, или так называемый упругий потенциал.

Выражение упругого потенциала было получено в предыдущей лекции и в матричном виде может быть записано следующим образом:

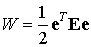
(6.4)

Как следует из соотношения (6.4) упругий потенциал представляет собой квадратичную форму относительно компонент вектора деформации. Запишем соотношение (6.4) в развернутом виде:

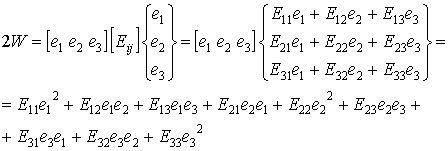
(6.5)

В данной формуле для сокращений записей были использованы индексные обозначения компонент вектора деформации:

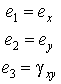
(6.6)

С учетом симметрии матрицы упругих модулей:

(6.7)

соотношение (6.5) может быть записано в виде квадратичной формы:

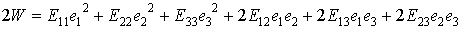
(6.8)

Применим теперь операцию варьирования к выражению потенциальной энергии деформации тела:

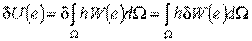
(6.9)

Отметим, что в данном случае потенциальная энергия является функцией деформаций, которые в свою очередь зависят от поля перемещений. Поэтому необходимо использовать правило варьирования сложной функции многих переменных:

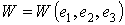
(6.10)

где перемещения являются независимыми варьируемыми функциями, а деформации – варьируемыми функциями, зависящими от перемещений.

Заметим также, что с формальной точки зрения математически операция вычисления вариации функции эквивалентна операции вычисления дифференциала функции, т.е. выполняется по тем же правилам:

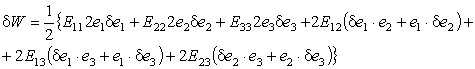
(6.11)

Перегруппировав слагаемые в соотношении (6.11), получим выражение 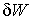в виде:

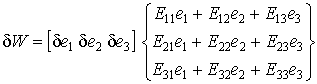
(6.12)

Окончательно вариация упругого потенциала может быть записана в следующем матричном виде:

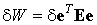
(6.13)

где 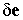- вариация вектора деформаций.

Тогда вариация потенциальной энергии деформации тела будет записана следующим образом:

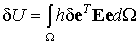
(6.14)

Вариация работы внешних сил находится простым варьированием соотношения (5.3, лекция 5) с учетом того, что варьируемой независимой функцией является поле перемещений:

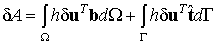
(6.15)

где 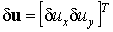- вариация вектора перемещений.

Заметим еще раз, что выражение (6.15) совпадает с выражением элементарной работы внешних сил на возможных перемещениях .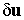

Вывод разрешающих уравнений

Согласно рассмотренному выше алгоритму конечно-элементной дискретизации область тела представляется в виде множества не пересекающихся подобластей. В соответствии с этим разбиением объемные и поверхностные интегралы, входящие в выражения потенциальной энергии и работы внешних сил, равны сумме интегралов по конечным элементам. Следовательно, интегральные соотношения (6.14) и (6.15) будут представлены в виде:

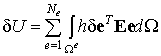
	(6.16)
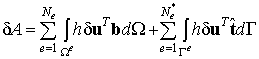
	(6.17)

где - общее число конечных элементов, 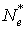- число конечных элементов, выходящих на границу области.

Для повышения универсальности рассматриваемого алгоритма введем в рассмотрение так называемые матрицы кинематических связей , состоящие из нулей и единиц. Введем также глобальный вектор узловых перемещений 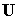, состоящий из декартовых координат векторов перемещений в узлах конечно-элементной сетки. При этом нумерация узлов сетки называется глобальной нумерацией, в отличие от локальной нумерации узлов на элементе. 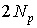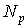Размер глобального вектора узловых перемещений равен , где - общее число узлов конечно-элементной сетки. Очевидно, что компоненты любого элементного вектора перемещений содержатся в соответствующих позициях глобального вектора перемещений. Матрицы кинематических связей как раз и устанавливают взаимосвязь между этими векторами на основе того очевидного факта, что любой узел любого элемента имеет свой локальный номер в пределах данного элемента и уникальный глобальный номер в пределах всей конечно-элементной сетки. Таким образом, связь между векторами может быть выражена следующим соотношением:

(6.18)

Когда формулы (5.6б) и (5.7б) лекции 5, представляющие собой перемещения и деформации в любой точке конечного элемента, могут быть представлены следующим образом:

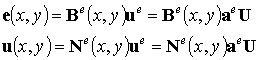
(6.19)

Соответственно вариации функци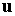й и вычисляются следующим образом:

,

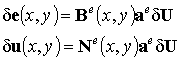(6.20)

поскольку именно глобальный вектор перемещений содержит независимые варьируемые функции – перемещения в узлах конечно-элементной модели. Обратим внимание, что несмотря на зависимость матрицы интерполирующих функций 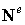и матрицы градиентов 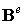от пространственных координат x и y, эти матрицы не являются варьируемыми функциями.

Применим операцию транспонирования к выражению (6.20). Согласно правилам вычисления транспонированной матрицы, представляющей собой произведение трех матриц, запишем:

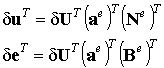
(6.21)

Подставим теперь выражения (6.21) и (6.19) в формулу вариации потенциальной энергии (6.16). Получим:

,

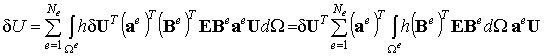(6.22)

где вектора 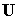и 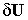вынесены за знаки суммы и интеграла, поскольку эти вектора состоят из независимых скалярных величин, матрицы , состоящей из нулей и единиц, вынесены только за знак интеграла, так как зависят от номера конечного элемента .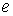

Введем следующие обозначения:

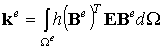,	(6.23)
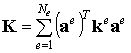,	(6.24)

где 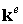называется элементной матрицей жесткости, 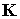называется глобальной матрицей жесткости. В результате получим компактное матричное выражение потенциальной энергии тела:

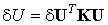
(6.25)

Аналогично предыдущему запишем выражение элементарной работы внешних объемных и поверхностных сил:

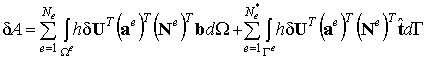
(6.26)

Введем стандартные обозначения элементных векторов сил:

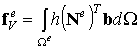,	(6.27)
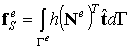,	(6.28)

где 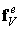называется элементным вектором узловых сил, статически эквивалентным заданным объемным силам, 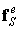называется элементным вектором узловых сил, статически эквивалентным заданным поверхностным силам.

Аналогично предыдущему элементные вектора сил объединяются в глобальные вектора:

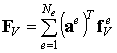,	(6.29)
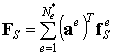,	(6.30)

где 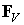называется глобальным вектором узловых сил, статически эквивалентным заданным объемным силам, 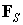называется глобальным вектором узловых сил, статически эквивалентным заданным поверхностным силам.

Отметим, что процесс формирования глобальной матрицы жесткости и глобальных векторов узловых сил в методе конечных элементов называется ансамблированием.

Таким образом, формула (6.26) будет представлена в следующем компактном виде:

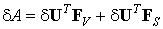
(6.31)

Подставим полученные выражения (6.25) и (6.31) в основную формулу принципа минимума потенциальной энергии Лагранжа (6.2):