Дифференциальное уравнение равновесия.

В теле, находящемся в напряженном состоянии, величина на­пряжений изменяется от точки к точке и является непрерывной функцией координат. Определим условия равновесия бесконечно малого параллелепипеда с ребрами dx, dy и dz, параллельными осям координат х, у, z (рис. 10), не являющимся главными. На­пряженное состояние точки а с координатами х, у, z определяет­ся напряжениями, действующими на гранях abcd, adb'c' и abd'c', и соответствующим им тензором напряжений:

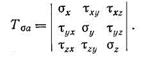
Напряженное состояние в точке а' определяется напряжени­ями, действующими на площадках 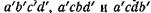. Эти напряжения отличаются от соответствующих напряжений в точ­ке а бесконечно малыми значениями. Интенсивность изменения напряжений при переходе от точки а к точке а' по какой-либо оси выражается частной производной этого напряжения по соответ­ствующей координате. Так, интенсивность изменения 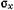по х

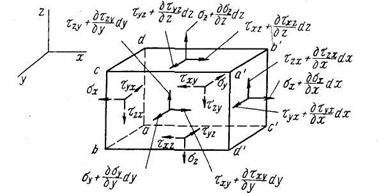
Рис. 11. Напряжения на гранях бесконечно малого параллелепипеда

После раскрытия скобок и сокращения на dxdydz получаем одно из уравнений равновесия. Проектируя силы на оси х, у и z, получаем дифференциальные уравнения равновесия, которые содержат 9 неизвестных функций.

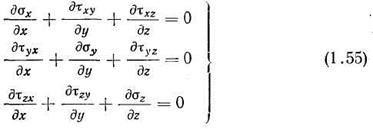
Благодаря свойству взаимности касательных напряжений, число неизвестных функций сокращается до 6 и все же задача определения напряжений является статически неопределимой. Для решения задачи вводят дополнительные уравнения, которые получают из рассмотрения физических свойств деформируемых материалов, в которых установлены зависимости между напряжениями и деформациями.

Дифференциальные уравнения равновесия являются основой при определении компонентов тензора напряжений в рассматриваемой точке пластически деформируемого тела.

ТОМД. Практические занятия по теме «Теория напряжений»

Некоторые понятия и формулы по теме «напряжения»

1) Октаэдрические напряжения .

Наряду с площадями, по которым действует σ и τ в теории ОМД рассматриваются площадки, равнонаклонённые к главным осям и следовательно отсекающие на них отрезки одинаковой длины. Эти площадки называются октаэдрическими. Всего таких площадок 8 , и вместе они образуют октаэдр. Эти площадки попарно взаимно параллельны , поэтому независимых площадок только 4. Напряжения действующие на октаэдрические площадки называют октаэдрическими: полное октаэдрическое напряжение Sокт;нормальное октаэдрическое: σ_окти касательное октаэдрическоенапряжение τ_окт.

S_окт= 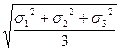= среднему гидростатическому напряжению.

Нормальное октаэдрическое напряжение: σ_окт = σ_ср =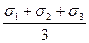

Октаэдрическое касательное напряжение τ_окт.

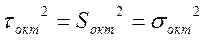
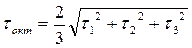
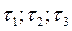-главные касательные напряжения