ПОНЯТИЕ О ТЕНЗОРЕ НАПРЯЖЕНИЙ

Напряженное состояние в точке деформируемого тела опре­деляется девятью векторами, тремя нормальными и шестью ка­сательными напряжениями. Совокупность этих девяти величин, характеризующих напряженное состояние точки тела, образует тензор

напряжения, который выражают в виде матрицы:

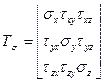
Если напряженное состояние задано в главных напряжениях, то тензор напряжений упрощается:

σ ₁ 0 0

Т_σ = 0 σ₂ 0

0 0 σ₃

Шаровой тензор, характеризующий изменение объема деформируемого тела, записывается в виде матрицы:

σ_ср 0 0

Т_σ = 0 σ_ср 0

0 0 σ_ср

Шаровой тензор описывает напряженное состояние точки, подвергнутой действию равномер­ного всестороннего сжатия или растяжения, когда касательные напряжения отсутствуют. Шаровой тензор может вызвать изме­нение объема при упругой деформации, но не изменение формы. Средним напряжением называется инвариант

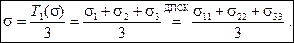
Физический смысл среднего напряжения: среднее напряжение и первый инвариант тензора напряжений определяют давление в индивидуальной частице сплошной среды, появление которого связано с изменением объема индивидуальных частиц.

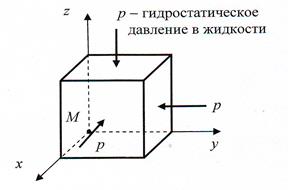
Рис.7. Схема действия сил шарового тензора при σ₁ = σ₂ = σ₃ и σ = -р

Вычтем из тензора напряжений шаровой тензор. Разность между тензором напряжений и шаровым тензором называется девиатором напряжений; он характеризует изменение формы деформируемого тела и определяется следующим выражением:

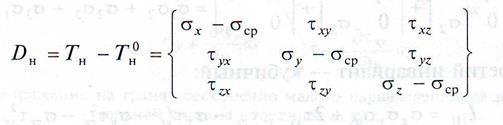
или в главных напряжениях:

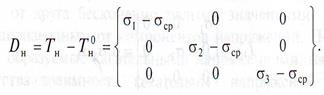
При формулировке свойств металла большое значение имеют инварианты девиатора тензора напряжений - скалярные величины, составленные из компонент тензора напряжений, не зависящие от выбора системы координат и не изменяющиеся при переходе от одной системы координат к другой.

Первый инвариант - линейный I₁ = σ₁ + σ₂ + σ₃ = const равен утроенному октаэдрическому нормальному напряжению или гидростатическому давлению

Второй инвариант – квадратичный I₂ = σ₁σ₂ + σ₂σ₃ + σ₃σ₁

Третий инвариант – кубический I₂ = σ₁σ₂σ₃

С тензорами можно производить различные математические действия.

.4. Октаэдрические напряжения.

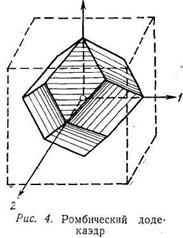
Наряду с площадками, по которым действует σ и τ в теории ОМД рассматриваются площадки, равнонаклонённые к главным осям и следовательно отсекающие на них отрезки одинаковой длины. Эти площадки называются октаэдрическими. Всего таких площадок 8 , и вместе они образуют октаэдр.

Эти площадки попарно взаимно параллельны , поэтому независимых площадок только 4. Напряжения действующие на октаэдрические площадки называют октаэдрическими: полное октаэдрическое напряжение Sокт;нормальное октаэдрическое: σ_окти касательное октаэдрическоенапряжение τ_окт.

S_окт= 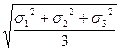= среднему гидростатическому напряжению.

Нормальное октаэдрическое напряжение: σ_окт = σ_ср =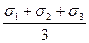

Октаэдрическое касательное напряжение τ_окт.

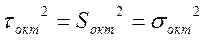
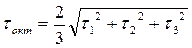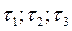где -главные касательные напряжения