Рівняння Лагранжа.

Рівняння Лагранжа першого роду

Лагранж запропонував та використав у механіці наступний аналітичний метод пошуку стаціонарних точок за допомоги методу невизначених множників. Отже, нехай на систему накладений зв'язок, що визначаються наступним рівнянням:

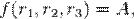
де A — константа. Тоді можна ввести рівняння Лагранжа першого роду, що виглядає наступним чином:

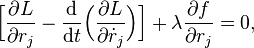
де λ — невизначений множник Лагранжа. Використовуючи варіаційну похідну 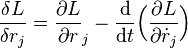від функції Лагранжа, можна переписати рівняння так:

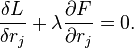
Для m рівнянь зв'язків fα існують множники Лагранжа для кожного з цих рівнянь, тож рівняння Лагранжа першого роду можна узагальнити наступним чином:

Рівняння Лагранжа (першого роду)

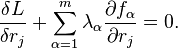Подібна процедура збільшує кількість рівнянь, але їх достатньо для знаходження усіх множників Лагранжа. Повна кількість рівнянь складається з кількості рівнянь зв'язків та кількості координат, тобто m + n. Перевага такого методу полягає у можливості оминути іноді доволі складну заміну змінних, що зв'язані рівняннями в'язів.

Існує зв'язок між рівняннями в'язів fα та силами їх реакції Nα, що діють у консервативній системі (тобто, сили є консервативними):

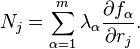
Рівняння Лагранжа другого роду[ред. • ред. код]

Рівняння Ейлера — Лагранжа[ред. • ред. код]

Для системи з N ступенями вільності рівняння Лагранжа містять N узагальнених координат і N узагальнених швидкостей. У лагранжевій механіці основними рівняннями руху є рівняння Лагранжа другого роду, або рівняння Ейлера — Лагранжа:

Рівняння Лагранжа (другого роду)

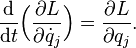Якщо у системі діють непотенціальні сили, рівняння Ейлера — Лагранжа матимуть наступний вигляд:

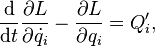
де 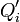— узагальнена непотенціальна сила.

Хоча математичний апарат лагранжевої механіки більш складний за ньютонівську механіку, рівняння Лагранжа дають більш глибоке розуміння сутності класичної механіки: наприклад, симетрії та законів збереження. На практиці набагато легше розв'язати рівняння Лагранжа, ніж рівняння Ньютона, оскільки лагранжев підхід потребує мінімальну кількість узагальнених координат з огляду на симетрію системи, а сили реакції зв'язків вже включені до геометрії системи. Для кожної узагальненої координати потрібне лише одне рівняння Лагранжа.

У системі багатьох частинок кожна частинка може мати свою, відмінну від інших кількість ступенів вільності. У кожному з рівнянь Лагранжа T являє собою повну кінетичну енергію системи, а V — повну потенціальну енергію.