Наближення сильно зв’язаних електронів.

Наближення сильного зв'язку - метод розв'язку рівняння Шредінгера для знаходження енергетичиних рівнівелектронів у кристалічному твердому тілі в одноелектронному наближенні, в якому хвильова функція електрона будується як лінійна комбінація хвильових функцій атомів.

Гамільтоніан, що описує рух електрона в періодичному потенціалі в твердому тілі можна записати у вигляді

,

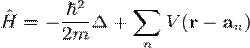де 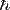- приведена стала Планка, m - маса електрона, 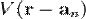- потенціальна енергія електрона, зумовлена взаємодією з n-тим атомом, 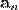- радіус-вектор n-го вузла.

Якщо функція 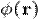є власною функцією гамільтоніана

,

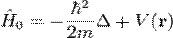із енергією 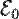, то в рамках методу сильного зв'язку хвильову функцію кристала шукають у вигляді

,

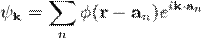який задовільняє умові теореми Блоха

Наближення сильного зв'язку застосовують тоді, коли інтегралом перекриття функцій 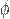, локалізованих на різних вузлах кристалічної ґратки можна знехтувати:

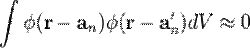при .

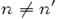Тоді закон дисперсії для електронних рівнів запишеться у вигляді

,

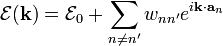де

.

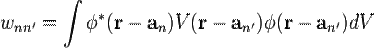Аналогічну процедуру можна провести з будь-якою атомною орбіталлю. Як наслідок атомний енергетичний рівень 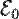розщеплюється при взаємодії електрона з іншими атомами кристала у вузьку зону.

Наближення найближчих сусідів[ред. • ред. код]

Атомні орбіталі 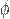швидко спадають із віддаллю, тож величини , які визначають ймовірність перестрибування електрона з одного вузла кристалічної ґратки на інший, можна вважати відмінними від нуля тільки для найближчих вузлів.

Наприклад, для простої кубічної ґратки з періодом a закон дисперсії електронних станів запишеться у вигляді

.

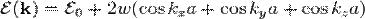Величина 2w визначає ширину зони.

Застосування[ред. • ред. код]

Наближення сильного зв'язку широко використовується в квантовій теорії твердого тіла, а також у квантовій хімії, де аналогічний метод часто називають методом Гюкеля.