Закони Кеплера.

Закони Кеплера - три емпіричні залежності, що описують рухпланет навколо Сонця. Названо на честь німецького астрономаЙоганеса Кеплера, який відкрив їх шляхом аналізу спостережень руху Марса навколо Сонця, здійснених данським астрономом Тихо Браге.

Перший закон Кеплера[ред. • ред. код]

Всі планети обертаються навколо Сонця еліптичними орбітами, в одному з фокусів яких перебуває Сонце (всі орбіти планет і тіл Сонячної системи мають один спільний фокус, в якому, власне, і розташовано Сонце).

Найближча до Сонця точка орбіти називається перигелієм, а найдальша від нього точка — афелієм.

Ступінь витягнутості еліпса характеризується його ексцентриситетом. Ексцентриситет дорівнює відношенню відстані фокуса від центра до довжини великої півосі (середньої відстані планети до Сонця). Коли фокуси й центр збігаються, еліпс перетворюється на коло. Орбіти планет — еліпси, які мало відрізняються від кіл; їх ексцентриситети малі. Наприклад, ексцентриситет орбіти Землі е = 0,017.

Другий закон Кеплера[ред. • ред. код]

Радіус-вектор планети (тіла Сонячної системи) за рівні проміжки часу описує рівновеликі площі.

Лінійна швидкість руху планети неоднакова в різних точках її орбіти: що ближча планета до Сонця, то більша її швидкість. Швид­кість руху планети у перигелії найбільша, а в афелії — найменша. Однак площа, яку "замітає" радіус-вектор за певний проміжок часу, не залежить від того, в якій частині орбіти перебуває планета. Площа, яку "замітає" радіус вектор за одиницю часу називаєтьсясекторною (сегментною) швидкістю.

Таким чином, другий закон Кеплера кількісно визначає зміну швидкості руху планети орбітою.

З погляду класичної механіки, другий закон Кеплера є проявом закону збереження моменту імпульсу.

Третій закон Кеплера[ред. • ред. код]

Квадрати зоряних періодів обертання планет відносяться, як куби великих півосей їхніх орбіт.

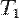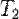На відміну від двох перших законів Кеплера, що стосуються властивостей орбіти кожної окремо взятої планети, третій закон пов'язує властивості орбіт різних планет між собою. Якщо сидеричні періоди обертання двох планет та , а довжини великих півосей їхніх орбіт, відповідно, 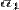та 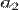, то виконується співвідношення:

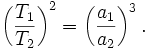
Цей закон Кеплера пов'язує середні відстані планет від Сонця з їхніми зоряними періодами обертання і надає змогу встановити відносні відстані планет від Сонця, інакше кажучи, дає змогу подати великі півосі всіх планетних орбіт в одиницях великої півосі земної орбіти.

Велику піввісь земної орбіти взято за астрономічну одиницю відстаней, але її абсолютне значення було визначено пізніше, лише у XVIII столітті.

Відношення кубу півосі до квадрата періоду обертання є сталою для всіх планет Сонячної системи і залежить лише від маси Сонця і гравітаційної сталої, як довів пізніше Ньютон:

.

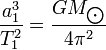Таким чином, це співвідношення дає можливість визначити масу Сонця.

Відхилення від законів Кеплера[ред. • ред. код]

З погляду фізики, закони Кеплера описують рух матеріальної точки навколо нерухомого центра мас у межах ньютонівської теорії гравітації. Насправді на рух планети впливає сила тяжіння не лише з боку Сонця, а й з боку інших планет. Сонце має скінченну масу, а отже центр Сонця також рухається внаслідок тяжіння планет. Крім того, ньютонівська теорія не враховує ефекти, які можна розрахувати лише у рамках загальної теорії відносності. Перелічені фактори призводять до збурень — невеликих відхилень фактичного руху планет від законів Кеплера.

2 Рух у центральному полі. Атом водню: енергетичний спектр, власні функції.

При дослiдженнi руху частинок у силових полях вирiзняється важливий клас сферично-симетричних потенцiалiв, тобто потенцiалiв U = U(r), якi залежать лише вiд модуля радiус-вектора r = |r|. Наслiдком центральної симетрiї поля є те, що гамiльтонiан частинки ˆH комутує з операторами квадрата моменту кiлькостi руху ˆL2, його проекцiї ˆLz та оператором iнверсiї ˆI. Це означає, що вiдповiднi величини є iнтеґралами руху. Отже, L2 = ~2l(l+1), l = 0, 1, 2, 3, . . ., Lz = ~m, число m набуває (2l + 1) значень вiд −l

до +l, а, як ми бачили в §34, парнiсть хвильової функцiї I = (−)l, тобто збiгається з парнiстю числа l. Крiм того, цi оператори комутують мiж собою i отже, мають спiльну систему власних функцiй. Важливо в цьому мiсцi зазначити, що в класичнiй механiцi задача про рух двох взаємодiючих мiж собою частинок зводиться

до проблеми одного тiла. Те ж є справедливим й у квантовiй механiцi.