Закони збереження енергії в електродинаміці.
Основними рівняннями, що описують поведінку електромагнітного поля і його взаємодія із зарядженими тілами є:
Рівняння Максвелла, що визначають поведінку вільного електромагнітного поля у вакуумі та середовищі, а також генерацію поля джерелами. Серед цих рівнянь можна виділити:
Теорема Гауса (закон Гауса) для електричного поля, що визначає створення електростатичного поля зарядами.
Закон замкнутості силових ліній магнітного поля (соленоїдного магнітного поля); він же — закон Гауса для магнітного поля.
Закон індукції Фарадея, що визначає генерацію електричного поля змінним магнітним полем.
Закон Ампера-Максвелла — теорема про циркуляцію магнітного поля з додаванням струмів зміщення, введених Максвеллом, визначає генерацію магнітного поля рухомими зарядами та змінним електричним полем.
Вираз для сили Лоренца, що визначає силу, що діє на заряд, який знаходиться в електромагнітному полі.
Закон Джоуля-Ленца, що визначає величину теплових втрат в провідному середовищі з кінцевою провідністю, при наявності в ній електричного поля.
Частковими рівняннями, що мають особливе значення є:
Закон Кулона — в електростатиці — закон, що визначає електричне поле (напруженість та/або потенціал) точкового заряду; також законом Кулона називається і подібна формула, яка визначає електростатичну взаємодію (силу, або потенцальну енергію) двох точкових зарядів.
Закон Біо-Савара — в магнітостатиці — основний закон, що описує породження магнітного поля струмом (аналогічний за своєю роллю в магнітостатиці закону Кулона в електростатиці).
Закон Ампера, що визначає силу, яка діє на елементарний струм, поміщений у магнітне поле.
Теорема Пойнтінга, що виражає собою закон збереження енергії в електродинаміці.
Закон збереження заряду.
Теорема Пойнтінга (англ. Poynting's theorem) — теорема, що описує закон збереження енергії електромагнітного поля. Теорема була доведена у 1884 році Джоном Генрі Пойнтінгом. Все зводиться до наступної формули:
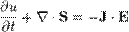 ,
,
Де S — вектор Пойнтінга, J — густина струму і E — електричне поле. Густина енергії 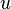 (
( 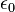 — електрична стала,
— електрична стала, 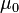 — магнітна стала).
— магнітна стала).
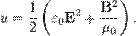
Теорема Пойнтінга в інтегральній формі:
 ,
,
де 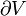 — поверхня, що обмежуює об'єм
— поверхня, що обмежуює об'єм 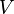 .
.
У технічній літературі теорема зазвичай записывается наступним чином ( 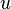 — густина енергії):
— густина енергії):
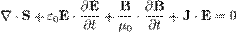 ,
,
где  — густина енергії електричного поля,
— густина енергії електричного поля,  — густина енергії магнітного поля і
— густина енергії магнітного поля і 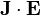 — потужність втрат Джоуля на одиницю об'єму.
— потужність втрат Джоуля на одиницю об'єму.
Теорема може бути доведена з допомогою двох рівнянь Максвелла (для простоти вважаємо, що середовище — це вакуум (μ=1, ε=1); для загального випадку з довільним середовищем потрібно у формули до кожного ε0 і μ0 приписати ε і μ):
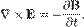
Домноживши дві частини рівняння на 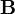 , отримаємо:
, отримаємо:

Розглянемо спочатку рівняння Максвелла-Ампера:
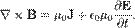
Домноживши дві частини рівняння на 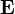 , отримаємо:
, отримаємо:
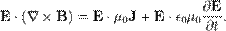
Віднявши перше рівняння з другого, отримаємо:
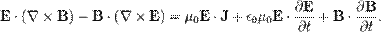
Нарешті:

Оскільки вектор Пойнтінга  визначається как:
визначається как:
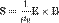
це рівнозначно:
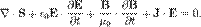
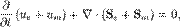
Дата добавления: 2015-06-01; просмотров: 1753;
