Ефект Зеємана у слабкому та сильному магнітних полях.

У 1896 р. П. Зеєман довів, що, коли помістити джерело світла між полюсами електромагніту, спектральні лінії джерела розщеплюються на ряд компонентів.

Ефектом Зеємана називають розщеплення спектральних ліній і рівнів енергії в зовнішньому магнітному полі.

При спостереженні випромінювання, яке поширюється перпендикулярно до напряму напруженості 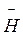магнітного поля, лінія ν0 симетрично розщеплюється на три компоненти з частотами ν+1, ν0 і ν-1. При цьому всі три компоненти лінійно поляризовані. Для середньої компоненти ν0, яку називають π-компонентою, коливання електричного вектора 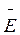напрямлені вздовж напруженості 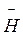зовнішнього магнітного поля. Для крайніх компонент ν+1 і ν-1 (так званаσ-компонента) коливання електричного вектора 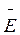перпендикулярні до напряму .

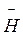При спостереженні випромінювання, яке поширюється вздовж напряму магнітного поля, лініяν0 зникає, а крайні лінії ν+1 і ν-1 виявляються поляризованими по колу з протилежними напрямами обертання. Такий тип розщеплення спектральних ліній називають нормальним, або простим, ефектом Зеємана. Для нього відстань між середньою і крайніми лініями нормального триплету Δν0 = ν+1 - ν0 = ν0 - ν-1 виявляється такою, що

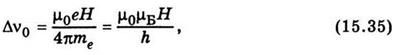де магнетон Бора; μ0 — магнітна стала. Нормальний ефект Зеємана відносно легко спостерігається в спектрах лужноземельних елементів, а також у спектрах Zn, Сd, Нg.

Нормальний ефект Зеємана пояснив ще X. Лоренц (1897 р.) на основі класичної електронної теорії. Квантово-механічна теорія ефекту Зеємана ґрунтується на аналізі розщеплення енергетичного рівня випромінювального електрона в атомі (розглядається атом з одним випромінювальним електроном), який вміщено в постійне магнітне поле з напруженістю 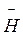. У випадку нормального ефекту Зеємана прийнято вважати, що електрон має тільки орбітальний магнітний момент 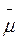m. У магнітному полі з індукцією 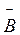електрон набуває додаткової енергії

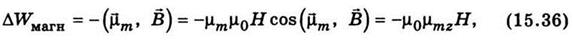
де μmz — проекція магнітного моменту на напрям z магнітного поля. Виходячи з формул (15.27) і (15.29), дістанемо

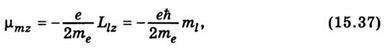
де ml — магнітне квантове число.

Отже, додаткова енергія, якої набуває електрон атома в магнітному полі,

Магнетон Бора μБ є одиницею виміру електронних магнітних моментів. Аналогічно цьому величина μ0μБH є одиницею виміру розщеплення енергетичних рівнів електронів у атомах, що перебувають у магнітному полі. Цю величину, що дорівнює розщепленню рівня ml = 1 за рахунок орбітального магнітного моменту електрона, називають нормальним розщепленням. Якщо позначити енергію електрона в атомі в деякому стані 1 у відсутності магнітного поля W1, а m1 — магнітне квантове число в цьому стані і відповідно W2 і m2 —

енергія електрона і магнітне квантове число в більш високому енергетичному стані, то повну енергію електрона в стані 1 і 2 за наявності зовнішнього магнітного поля можна записати так:

Частота оптичного переходу між станами 2 і 1 буде

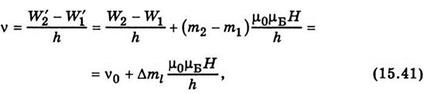
де ν0 — частота спектральної лінії у відсутності зовнішнього магнітного поля. За правилом добору для магнітного квантового числа, при переходах між дозволеними рівнями Δml= m2 - m1 = +1, 0, -1. Тому частоти нормального триплету Зеємана мають такі значення:

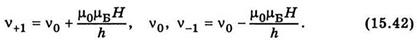
Ці значення збігаються з дослідом у разі сильних магнітних полів. Критерій сильного і слабкого магнітного поля в ефекті Зеємана пов’язаний з нормальним розщепленням μ0μБH. Якщо ця величина набагато перевищує різницю між енергіями двох енергетичних рівнів i-го і j-го у відсутності магнітного поля

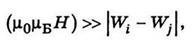
то магнітне поле вважають сильним (Wi і Wj — енергії двох рівнів у атомі). Магнітне поле, що задовольняє протилежну умову 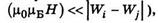називають слабким.

У слабкому магнітному полі спостерігається аномальний або складний ефект Зеємана. У цьому разі спектральні лінії розщеплюються на кілька компонент, які належать за своєю поляризацією або до π-, або до σ-компонент. Аномальний ефект Зеємана дістав своє тлумачення після виявлення спіну електрона. При поясненні нормального ефекту Зеємана береться до уваги лише орбітальний магнітний момент електрона. Наявність у електрона спіну і власного магнітного моменту ускладнює картину розщеплення енергетичних рівнів і спектральних ліній у магнітному полі.

При збільшенні напруженості магнітного поля взаємодія між орбітальним та спіновим моментами стає все менш істотною порівняно із взаємодією кожного з них окремо із зовнішнім полем. Розщеплення спектральних ліній при цьому зростає і поступово починають зливатися компоненти мультиплетів сусідніх спектральних ліній. У сильному магнітному полі з усіх компонент мультиплетів залишаються три лінії для нормального (поздовжнього) ефекту Зеємана. Перехід від аномального до нормального ефекту Зеємана при збільшенні напруженості зовнішнього магнітного поля називають ефектом Пашена — Бака.

У 1913 р. Й. Штарк відкрив явище розщеплення спектральних ліній в електричному полі для бальмерівської серії гідрогену. Це явище розщеплення енергетичних рівнів і спектральних ліній під дією на речовину зовнішнього електричного поля називають ефектом Штарка. Вплив електричного поля на атом істотно залежить від того, чи має він електричний момент 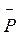l, чи такого моменту немає. Якщо 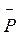l ≠ 0 (ця умова виконується, наприклад, для станів з n > 1 у атома гідрогену і гідрогеноподібних йонів), то у зовнішньому електричному полі з напруженістю 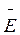такий атом-диполь набуває додаткової енергії, яка пропорційна напруженості поля,

Ця додаткова енергія і спричинює лінійний ефект Штарка.

Якщо дипольний електричний момент атома у відсутності зовнішнього електричного поля дорівнює нулю, то спостерігається квадратний ефект Штарка, при якому розщеплення енергетичних рівнів і відповідно спектральних ліній пропорційне квадрату напруженості електричного поля. Причину цього явища можна пояснити так: під дією зовнішнього поля атоми поляризуються, причому в не дуже сильному полі, індукований дипольний момент 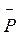l стає пропорційним напруженості поля:

де α — поляризованість атома. Додаткова енергія, якої набуває атом в електричному полі,

Ця енергія і спричинює квадратичне штарківське розщеплення енергетичних рівнів і спектральних ліній. Квадратичне розщеплення набагато менше, ніж розщеплення у випадку лінійного ефекту Штарка.